Correction du controle 4 niveau 6e herve

Correction du contrôle 4 niveau 6e
Calcul rapide :2 min
2,2 + .3,8 = 6 6,3 - .1,8. = 4,5
56 000÷1000
=
56
34÷10.
= 3,4
9×7
= 63
13 + 15 + 27 = 55
on ajoute 13 et 27
et au résultat on
ajoute 15
21×25
= 525
on multiplie 21
par 100 soit 2100,
on divise 2 100
par 2 soit 1 050
puis on divise1050
par 2 soit 525
125×5
= 625 On
multiplie 125 par 10
soit 1 250 puis on
divise le résultat par
2
43×200
=
8 600
70÷5
= 14
On multiplie 70
par 2 puis on
divise le résultat
par 10
Calcul posé : 8 min
Donner l'ordre de grandeur puis poser et effectuer les quatre opérations suivantes:
A = 13,25 + 5,72 + 23,685 B = 135,8 – 26,64
C =
8,35×0,18
D =
1489,28÷37
(quotient avec deux chiffres après la virgule)
Si vous avez des erreurs poser vos opérations les refaire puis vérifier à la calculette
Applications:
Exercice 1:
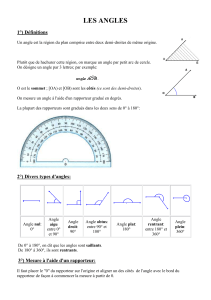
1- Deux élèves souhaitent mesurer des angles. Hervé veut mesurer l'angle grisé et José souhaite mesurer
l'angle
BAC .
Peuvent-ils effectuer une mesure correcte ? Si oui, indique la mesure de l'angle et si non, explique pourquoi..
Hervé
Hervé n'a pas correctement posé correctement le rapporteur car le sommet de l'angle n'est pas au
centre du rapporteur
José a bien mis le sommet de l'angle au centre du rapporteur mais il n'a pas mis le côte [AB) sur
l'origine de la graduation mais il peut mesurer l'angle par soustraction . Il lit la mesure de
xAC
puis celle
de
Bax
et il soustrait la mesure de
Bax
à celle de
xAC
BAC = xAC – xAB
A
B
C
1 3 0
5 0
1 0
1 7 0
20
1 6 0
40
1 4 0
30
1 5 0
60
1 2 0
5 0
1 3 0
70
1 1 0
8 0
1 0 0
90
0
1 8 0
1 8 0
0
1 7 0
1 0
1 6 0
20
1 5 0
30
1 4 0
4 0
1 2 0
60
1 1 0
70
1 0 0
80
centre du
rapporteur
x

2- Pour chaque angle, j'indique s'il est aigu ou obtus. Je lis ensuite sa mesure sur la bonne graduation du
rapporteur.
Le premier angle est aigu et sa mesure est de 50°.
Le second est obtus et sa mesure est de 110°
Exercice 2: Paul a fait ses calculs mais il a oublié ou mal placé sa virgule. Je corrige, si nécessaire,
ses erreurs sur cette feuille.
A =
12,8×5,3
= 6 784 B =
8,6÷2
= 0, 43
Pour A, l'ordre de grandeur est de 60 Pour B, l'ordre de grandeur est de 4
A =
12,8×5,3
= 6 7,84 B =
8,6÷2
= 4,3
C = 37 ,5 + 67,57 = 1050,7 D = 793,05 – 310,167 = 482,883
Pour C, l'ordre de grandeur est de 100 Pour D, l'ordre de grandeur est de 400
C = 37 ,5 + 67,57 = 105,07 Le résultat est correct
Exercice 3 :
1) Je construis un triangle ABC tel que BC = 5 cm,
ABC =30 °
et
ACB
= 50 °.
2) Je construis au compas le point F symétrique du point A
par rapport à la droite (BC) .
3) Que peux -tu dire de la droite (BC) pour l'angle
ABF
?
Je justifie.
Données Propriété Ce que je déduis
Les points A et F sont
symétriques par rapport à la
droite (BC) et les points B et C
sont sur l'axe de symétrie donc
le symétrique du point B est le
point B et le symétrique du
point C est le point C
L'image de l'angle
CBA
est
CBF
Si deux angles sont symétriques
alors ils ont la même mesure
CBA
=
CBF
Les angles sont adjacents et de
même mesure donc la demi-
droite [BC) est la bissectrice
de l'angle
ABF
1 3 0
50
10
1 7 0
2 0
1 6 0
4 0
1 4 0
3 0
1 5 0
60
1 2 0
5 0
1 3 0
70
1 1 0
8 0
1 0 0
90
0
1 8 0
1 8 0
0
1 7 0 10
1 6 0
2 0
1 5 0
3 0
1 4 0
40
1 2 0
60
1 1 0
7 0
1 0 0
8 0
1 3 0
5 0
10
1 7 0
2 0
1 6 0
40
1 4 0
3 0
1 5 0
60
1 2 0
50
1 3 0
70
1 1 0
80
1 0 0
90
0
1 8 0
1 8 0
0
1 7 0
1 0
1 6 0
2 0
1 5 0
30
1 4 0
40
1 2 0
60
1 1 0
7 0
1 0 0
80

4) Je calcule la mesure de l'angle
ABF
Données Propriété Ce que je déduis
CBA
= 30°
(CB) est la bissectrice de l'angle
ABF
La bissectrice d'un angle est la
droite qui partagze l'angle en
deux angles adjacents et
superposables
ABF
=
2× CBA
ABF
=
2×30
ABF
= 60°
Exercice 4:
L'égalité: 879 =
37×23
+ 28 est-elle l'égalité de la division euclidienne de
879 par 23 ou de 879 par 37. J'explique mon choix.
Dans l'égalité donnée je vois que le reste de la division est 28 donc le diviseur est supérieur à
28 et par conséquent, nous avons la division euclidienne de 879 par 37
Partie 2: Calculette autorisée
Objectifs:
Bilan
acquis en cours
d'acquisition
non
acquis
1- Je sais mettre en œuvre une démarche de raisonnement sur un problème
2- Je sais lire un dessin codé et en extraire des figures
3- Je sais reconnaître des symétriques sur un dessin codé
4- Je sais écrire un raisonnement de géométrie en trois colonnes
Problème1:
Antoine possédait 832,28 € sur son livret d'épargne. Pour son anniversaire ses parent lui ont déposé
75 €. Comme il voulait se faire plaisir, il a retiré de l'argent pour s'acheter une paire de baskets à
35 € et une tenue de sport à 148,50 €.
Données: argent qu'il a sur son livret d'épargne: 832,28 €
Somme que lui donne ses parents : 75 €
Sommes dépensées : 35 € et 148,50 €
Je cherche combien il lui reste sur son livret d'épargne.
Montant de ses dépenses:
35 + 148,50 = 183,50
Somme qu'il a sur son livret d'épargne:
832,28 + 75 = 907,28
Ce qui lui reste:
907,28 – 183,50 = 723,78
Il lui reste 723,78 €
Problème 2: Voici un calcul:
17×53×2÷7
=
856÷7
= 13
Trouver un texte de problème dont la solution est le calcul ci-dessus.

Problème 3:
1) En observant le dessin, je peux dire
a) que le quadrilatère ABCD est un rectangle car il a quatre
angles droits
b) que le quadrilatère OJML est un losange car il a quatre
côtés égaux
2) a) Ce dessin admet deux axes de symétrie. Les axes
de symétries sont les droites (JL) et (OM)
b) Le symétrique du point J par rapport à l'axe (OM)
est le point L et par rapport à l'axe (JL) c'est le point J lui-même
3) Je vois que les droites (OM) et (AD)sont parallèles. J'écris la démonstration en trois
colonnes.
Données Propriété Conclusion
La droite ( AD) est
perpendiculaire à le droite (AB)
La droite ( OM) est
perpendiculaire à le droite (AB)
Si deux droites sont
perpendiculaires à la même
droite alors elles sont parallèles
Donc les droites (AD) et (OM)
sont parallèles.

Correction du contrôle 4 niveau 6e ( deuxième version
Calcul rapide :2 min
2,4 + .3,6 = 6 6,1 - .1,6. = 4,5
65 000÷1000
=
65
34÷100.
=
0,34
9×8
= 72
23 + 15 + 27 = 65
on ajoute 23 et 27
et au résultat on
ajoute 15
31×25
= 775
on multiplie 31
par 100 soit 3100,
on divise 3 100
par 2 soit 1 550
puis on divise
1 550 par 2 soit
775
128×5
= 640 On
multiplie 128 par 10
soit 1 280 puis on
divise le résultat par
2
34×200
=
6 800
80÷5
= 16
On multiplie 80
par 2 puis on
divise le résultat
par 10
Calcul posé : 8 min
Donner l'ordre de grandeur puis poser et effectuer les quatre opérations suivantes:
A = 33,25 + 6,725 + 32,68 B = 235,8 – 76,64
C =
9,35×0,28
D =
2489,28÷38
(quotient avec deux chiffres après la virgule)
Si vous avez des erreurs poser vos opérations les refaire puis vérifier à la calculette
Applications:
Exercice 1:
1- Deux élèves souhaitent mesurer des angles. Hervé veut mesurer l'angle grisé et José souhaite mesurer
l'angle
BAC .
Peuvent-ils effectuer une mesure correcte ? Si oui, indique la mesure de l'angle et si non, explique pourquoi..
Hervé
Hervé n'a pas correctement posé correctement le rapporteur car le sommet de l'angle n'est pas au
centre du rapporteur
José a bien mis le sommet de l'angle au centre du rapporteur mais il n'a pas mis le côte [AB) sur
l'origine de la graduation mais il peut mesurer l'angle par soustraction . Il lit la mesure de
xAC
puis celle
de
Bax
et il soustrait la mesure de
Bax
à celle de
xAC
BAC = xAC – xAB
A
B
C
1 3 0
5 0
1 0
1 7 0
20
1 6 0
40
1 4 0
30
1 5 0
60
1 2 0
5 0
1 3 0
70
1 1 0
8 0
1 0 0
90
0
1 8 0
1 8 0
0
1 7 0
1 0
1 6 0
20
1 5 0
30
1 4 0
4 0
1 2 0
60
1 1 0
70
1 0 0
80
centre du
rapporteur
x
Sur votre feuille
les dessins sont
inversés