Q2 : Qu`est ce qu`une onde mécanique

EXERCICE 1 : QUESTION DE COURS
Q1 : Qu’est ce qu’une onde progressive ?
Q2 : Qu’est ce qu’une onde mécanique ?
Q3 : Qu’elle est la condition pour qu’une onde soit diffractée ?
Q4 : Quelles sont les différentes sources de rayonnement dans l’univers ?
Q5 : Qu’est ce que l’intensité sonore ?
Q6 : Comment calcule t-on l’intensité sonore à partir du niveau d’intensité ?
Q7 : Qu’est ce que l’effet Doppler ?
Q8 : Quelle est la condition pour qu’un mouvement rectiligne soit uniformément varié ?
Q9 : Quelle est la condition pour qu’un mouvement rectiligne soit uniforme ?
Q10 : Enoncer la troisième loi de Newton

Exercice 2 : Saut en tremplin.
Le 17 mars 2013, le norvégien MADS OTSBERG a réalisé le saut le plus long du monde sur piste
enneigée au volant de sa Ford fiesta RS WRC lors d’un festival de sports extrêmes à TRYSIL en
NORVEGE. Après une phase d’accélération, son véhicule a abordé le tremplin avec une vitesse de
145 km.h-1 et s’est envolée pour un saut d’une portée de plus de 60 m.
Dans tout l’exercice, le système voiture et cascadeur est assimilé à son centre d’inertie G.
L’étude est faite dans le référentiel terrestre considéré comme galiléen.
On pose h = OC (hauteur du tremplin)= 8 m
Données :
Intensité de la pesanteur : g = 9,81 m.s-2
Masse du système : m = 1 100 kg
Longueur du tremplin de lancement = 31 m.
Le cascadeur aborde le tremplin au point B, avec une vitesse de 145 km.h-1 et maintient cette vitesse jusqu’au point C.
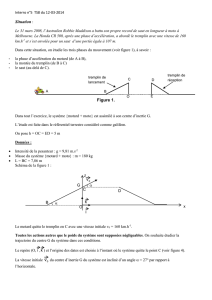
Le repère d’étude (O,
i
,
k
) est indiqué sur la figure .
Le tremplin est incliné d’un angle par rapport à l’horizontale.
Le cascadeur quitte le tremplin en C avec une vitesse initiale v0 =145 km.h-1.
Toutes les actions autres que le poids du système sont supposées négligeables. On souhaite étudier la trajectoire du centre
G du système dans ces conditions.
Le repère (O,
i
,
k
) et l’origine des dates sont choisis à l’instant où le système quitte le point C .
La vitesse initiale
0
v
du centre d’inertie G du système est inclinée d’un angle par rapport à l’horizontale.
Q1. En appliquant la deuxième loi de Newton, donner les équations horaires x(t) et z(t) du mouvement du point G.
Q2. En déduire l’équation de la trajectoire z(x).
Q3. A quelle hauteur maximale par rapport au sol le cascadeur va-t-il se trouver lors de son saut ?
Q4. A quelle distance maximale de C doit se trouver le point D pour que « l’atterrissage » se fasse sur le tremplin ?
Q5. Comparer cette valeur avec celle donnée dans l’énoncé. Comment peut-on interpréter cet écart ?
0
v
B
D
x
G
C
z
O
i
k
figure

Exercice 3 : Etude d’une Tablette Tactile HP TouchPad
(Numérisation et transfert de donnée)
Document 1 : Fiche technique Tablette Tactile HP TouchPad
Document 2 : Numérisation d’une image
Le codage de l’image
Le mode de représentation RVB (qui signifie rouge, vert,
bleu) est le plus utilisé pour la restitution de l’image. On l’utilise
notamment pour les caméras ou pour les écrans TV. L’image est
composée d’une matrice de points appelés pixels (Picture Elément).
Un pixel est composé de trois couleurs: le rouge, le vert et le
bleu. Le mode de composition des couleurs se fait par addition des
couleurs. En jouant sur l’intensité de chacune d’entre elle, on peut
recréer les autres couleurs.
Codage : chaque pixel de l’image est codé sur un certain nombre de
bits.
Ainsi, si on code sur 8 bits, on obtient des images en 256 niveaux de
gris, en 24 bits (codage RVB), on obtient des couleurs dites vraies
(truecolor).
Note : la composante alpha, qui permet d’inclure des informations
supplémentaires à l’image (comme la transparence), peut être
ajoutée. Le codage se fait alors en 32 bits (RGBA).
Q1. À partir de la fiche technique (document 1) de la Tablette tactile fourni ci-dessus, donner la résolution maximale de
l'écran. En déduire le format de l’écran (4/3 ou 16/9). Justifier votre réponse.
Q2. Relever la diagonale de l’écran et la convertir en cm (1 pouce = 2,54 cm).
En déduire la largeur et la hauteur de l’écran.
Q3. En déduire la taille d’un pixel en mm.
Rouge
Vert
bleu

Q4. On considère que la surface moyenne d’un doigt sur un écran tactile correspond à un 1cm². Calculer la dimension du
carré en pixels sur l’écran (arrondir au pixel supérieur). En déduire le nombre de pixels couvert par le doigt.
Q5. Calculer le nombre de pixels de l’écran tactile de notre tablette.
Q6. À partir du nombre de pixels, calculer le débit de données minimum pour cet écran avec une fréquence de
rafraichissement de 100 Hz (100 images par seconde).
Q7. La couleur de chaque pixel est constituée de trois composants RVB : le rouge, le vert et le bleu.
Chaque couleur est déterminée par huit bits de donnée.
Calculer le nombre de teintes possibles par couleur et en déduire le nombre de couleurs différentes pouvant être
affichées par chaque pixel.
Q8. Un des pixels de l’écran est codée en décimal pour chaque couleur R V B comme indiqué ci-dessous, donnez en la
correspondance en binaire et en Hexadécimal, puis indiquer la couleur de ce pixel.
Q9. On désire envoyer par Wifi à une imprimante une photo prise par la caméra frontale de la tablette, quelle sera la taille
du fichier numérique généré en octet sachant que l’on utilise le codage RVB.
Q10. Combien de temps faut-il pour envoyer ce fichier si la connexion Wifi de la tablette à un débit de transfert de 4Mio/s.
Calculer la taille de ce fichier en Mio, et déterminer la durée de l’envoi de celui-ci par Wifi.
EXERCICE 4 : Fibre optique à saut d’indice.
Une fibre optique à saut d'indice (représentée sur la figure 1) est formée d'un cœur cylindrique en verre de diamètre
ф cœur = 50 µm, d'axe Ox et d'indice nc =1,54, entouré d'une gaine optique d'indice ng = 1,52.
Un rayon situé dans le plan Oxy entre dans la fibre au point O avec un angle d'incidence θ.
R
V
B
Codage décimal
210
190
10
Codage binaire %
Codage Hexadécimal $

Q 1. A quelle condition sur i, angle d'incidence à l'interface cœur/gaine, le rayon reste-t-il confiné à l'intérieur du cœur ?
On note iL l'angle d'incidence limite, donnez en sa valeur.
Dessiner sur la feuille (document réponse) le trajet ultérieur du rayon en faisant apparaître plusieurs réflexions.
Q 2. Montrer que la condition précédente est vérifiée si l'angle d'incidence θ est inférieur à un angle limite θL tel que
sin(θL) = nc . cos(il).
On rappelle que sin2x + cos²x = 1 pour tout réel x. En déduire l'expression de l'ouverture numérique ON de la fibre, définie
par ON = sin(θL), en fonction de nc et ng uniquement.
Q 3.Calculer la valeur de cette l’ouverture numérique nc = 1,54 et ng = 1,52.
Q4. Un rayon entre dans la fibre optique au point O avec un angle d'incidence limite θL, calculer la distance OA.
Q5. Calculer la distance OC puis le rapport OA/OC.
En déduire la distance parcourue par le rayon dans la fibre si celle-ci fait 1 Km de long.
Q6. Exprimer la vitesse de propagation de la lumière dans le cœur de la fibre en fonction de la vitesse de la lumière dans le
vide, notée c, et l'indice nc du cœur.
Q7. Calculer la différence de temps de parcours ∆t entre ce rayon et un rayon qui parcourrait la fibre sur l’axe Ox.
On donne la vitesse de la lumière dans le vide : c = 3,00.108 m.s−1.
Q8. Déterminer la fréquence maximale de répétition pour que les impulsions ne se recouvrent pas en bout de fibre.
Q9. On injecte à l'entrée de la fibre une impulsion lumineuse de durée t0 formée par un faisceau de rayons ayant un angle
d'incidence compris entre 0 et θL. La figure 2 représente l'allure du signal lumineux en fonction dutemps. Reproduire la
figure sur la feuille (document réponse) en ajoutant à la suite l'allure du signal lumineux à la sortie de la fibre.
Quelle durée a approximativement l'impulsion lumineuse en sortie de fibre?