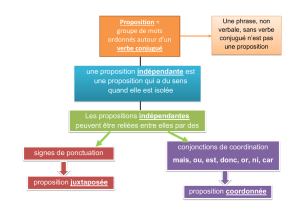
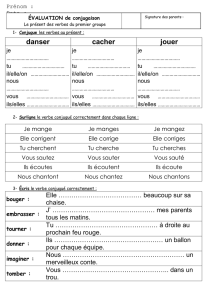
Contrôle et validation des calculs numériques Partie 1 : Algèbre

Contrôle et validation des calculs numériques
TP1 - Mise en place du gradient conjugué préconditionné
Université de Caen Basse-Normandie
Le but du TP est de mettre en place la méthode du gradient conjugué, il s’agit d’une méthode itérative très répandue
permettant la résolution de systèmes matriciels de type Ax =bavec Asymétrique définie positive. La convergence
d’une telle méthode est rapide (au plus nitérations où nest la dimension de A). Cependant, un préconditionnement
de la matrice par une autre matrice Cpermet de diminuer encore le nombre d’itérations.
Partie 1 : Algèbre linéaire sous C++
Le langage C++ est un code de programmation permettant (entre autre !) la mise en place d’algorithmes de réso-
lution. Dans le cas présent, nous nous intéressons à la résolution de systèmes matriciels de type Ax =boù Aest
une matrice symétrique définie positive. La compilation des fichiers textes contenant le code (de type .c ou .cpp)
s’effectue à l’aide du compilateur g++, nous écrirons dans un terminal :
g++ monfichier.cpp -o monfichier
Le compilateur g++ traduit le fichier texte monfichier.cpp et le compile afin de créer un fichier exécutable appelé
monfichier.
1. Ecrire un programme permettant de lire et écrire un vecteur sur un terminal.
2. Ecrire des fonctions pour réaliser la somme, la différence et le produit scalaire de deux vecteurs.
3. Reprendre les deux premières questions dans le cas d’une matrice.
4. Ecrire des fonctions pour effectuer le produit entre un vecteur et un scalaire, entre une matrice et un scalaire,
et une matrice et un vecteur.
Partie 2 : Algorithme du gradient conjugué préconditionné
1. Ecrire en langage C++ l’algorithme du gradient conjugué (voir au dos).
2. Utiliser différents types de conditionnements (Jacobi, SSOR, factorisation de Cholesky, ...). Tester votre pro-
gramme avec CADNA.

Algorithme du gradient conjugué
Algorithm 1 Evaluate xsuch that Ax =b
Ensure: ε= 1e−6nmax = 1000
n←0
g←Ax −b
Cg ←C×g
h← −Cg
g2←Cg0×g
while (n≤nmax )&(||g2|| > ε)do
Ah ←A×h
ρ←−g0×h
Ah0×h
x←x+ρ×h
g←g+ρ×Ah
Cg ←C×g
g2p←g2
g2←Cg0×g
γ←g2
g2p
h←γ×h−Cg
end while