Télécharger

I2 Lois de l’induction
Exercices de cours
Exercice 1 Application de la loi de FaradayExercice 1 Utiliser la loi de Faraday
Évaluer qualitativement la variation du flux d’un champ magnétique
On approche le pôle nord d’un aimant d’une spire. On a choisi
d’orienter la spire comme indiqué sur le schéma.
(1) En raisonnant sur les lignes de champs créées par un aimant,
donner le signe puis le sens de variation du flux magnétique
extérieur à travers la spire.
(2) Dessiner un schéma électrique équivalent en plaçant la force
électromotrice induite.
(3) En déduire le sens réel du courant idans le circuit.
(4) Quel est le sens du champ magnétique créé par la spire?
SUD NORD
i
−→
S
−→
vaimant/spire
Exercice 2 Inductance propre d’un bobine longueExercice 2 Évaluer le flux d’un champ magnétique
Évaluer l’inductance propre d’une bobine longue
On considère une bobine très longue telle que l’on puisse négliger les effets de bords (on peut considérer la bobine infinie) composée de
N=1,0 ·103spires, parcourue par un courant i.
Les caractéristiques de la bobine sont les suivantes: section S=1,0 ·10−3m2, longueur l=0,10 m.
Le champ magnétique dans la bobine est quasi-uniforme de norme B=µ0
N
li
(1) Faire un schéma et orienter les surfaces décrites par chaque spire, on placera en particulier un vecteur unitaire. En déduire
l’expression du champ magnétique −→ Bà l’intérieur de la bobine longue.
(2) Calculer le flux propre à travers une spire puis à travers les N spires de la bobine.
(3) En déduire la valeur du coefficient d’auto-inductance Lde la bobine.
Exercice 3 Énergie stockée dans le champ magnétiqueExercice 3 Réaliser un bilan énergétique
On reprend l’exercice précédent. Exprimer la force électromotrice induite en précisant la convention utilisée. En déduire la puissance puis
l’énergie stockée sous forme magnétique dans la bobine. On supposera qu’aucune énergie magnétique n’est stockée lorsque la bobine
n’est parcourue par aucun courant.
Exercice 4 Calcul d’une inductance mutuelleExercice 4 Déterminer l’inductance mutuelle pour des bobines en influence totale
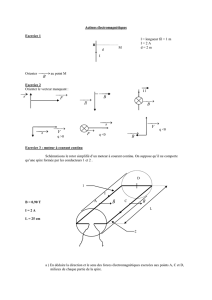
On considère deux bobines longues, l’une, parcourue par le courant iint, est placée à l’intérieur de l’autre, parcourue par le courant iext.
On note Sint et Sext les sections respectives des bobines, Nint et Next leur nombre de spires. On suppose que les deux bobines ont la même
longueur l.
On suppose que les bobines sont suffisamment longues pour que le champ que chacune d’entre elle crée est nul à l’extérieur et vaut
Bi=µ0
Ni
li
iià l’intérieur. L’indice iest soit int ou ext selon la bobine considérée et le champ est orienté dans le sens conventionnel des
spires.
(1) Exprimer le flux magnétique φext→int que crée la bobine extérieure à travers la bobine intérieure.
(2) Même question pour le flux magnétique φint→ext que crée la bobine intérieure à travers la bobine extérieure.
(3) Exprimer le coefficient d’inductance mutuelle et montrer que les deux flux magnétiques donnent la même expression de ce coeffi-
cient.
1

I2: Lois de l’induction Exercices de cours
Exercice 5 Circuits couplés par inductance mutuelleExercice 5 Établir le système d’équation couplé (inductance mutuelle)
On considère les deux circuits suivants couplés par induction
mutuelle, fixes dans le référentiel d’étude. Le coefficient Mest le co-
efficient d’inductance mutuelle entre les deux circuits, L1et L2sont
les inductances propres totales des deux circuits. On a représenté ces
inductances propres sous la forme de bobines idéales.
E1
i1
L1
R1
E2
i2
L2
R2
M
(1) Exprimer le flux magnétique à travers le circuit 1 et en déduire la force électromotrice induite e1dans ce circuit.
(2) Même question dans le circuit 2. On notera e2la force électromotrice induite dans ce circuit.
(3) Tracer un schéma équivalent pour chaque circuit et en déduire les deux équations différentielles vérifiées par les courants.
(4) Les écrire en régime sinusoïdal forcé à la pulsation ω.
Exercice 6 Transformateur de tension parfaitExercice 6 Établir la loi des tensions
i1i2
U1U2
Deux bobines sont enroulées autour d’un cadre métallique ferromagnétique.
•L’enroulement de gauche est appelé l’enroulement primaire: la tension à ses bornes est notée U1, il est parcouru par un courant i1
et contient N1spires identiques. Les grandeurs électriques sont sinusoïdales.
•L’enroulement de droite est appelé l’enroulement secondaire: la tension à ses bornes est notée U2, il est parcouru par un courant i2
et contient N2spires identiques. Les grandeurs électriques sont sinusoïdales.
•Le cadre ferromagnétique sert à canaliser les lignes de champ magnétique de façon à ce que le flux qui traverse une spire du primaire
soit le plus proche possible de celui qui traverse une spire du secondaire. On supposera que le couplage est parfait c’est-à-dire que
ces flux sont égaux. On note φle flux traversant une spire, orientée positivement dans le sens de la flèche en pointillé.
Le circuit primaire est relié à un générateur, il crée alors un flux magnétique dans le cadre. Ce flux magnétique est dirigé vers le circuit
secondaire où il crée un courant dans le circuit secondaire (une tension).
Nous allons chercher le lien entre U1et U2en négligeant tout effet résistif dans le circuit, toute perte magnétique dans le cadre et tout
courant induit dans le cadre.
(1) Exprimer le flux magnétique φ1traversant l’enroulement primaire en fonction de φet N1. Faire de même pour le flux magnétique
φ2traversant l’enroulement secondaire.
(2) Calculer les forces électromotrices et dessinez le schéma équivalent.
(3) En déduire alors la relation entre U1et U2.
(4) Le primaire est branché sur le secteur américain, à 110V. On souhaite brancher sur le secondaire un appareil français (fonctionnant
donc sur du 220V). Comment doit-on choisir le nombre d’enroulements des circuits?
2/4

I2: Lois de l’induction Exercices de cours
Exercice 7 Rails de Laplace: GénérateurExercice 7 Interpréter qualitativement les phénomènes
Établir les équations mécaniques et électriques
Effectuer un bilan énergétique
On reprend le dispositif des rails de LAPLACE mais cette fois-ci,
au lieu d’être branché sur un générateur, le circuit comporte un am-
pèremètre. Un opérateur tire la barre mobile avec la force Fop
−→
ex. Ce
dispositif modélise avec une géométrie simple le principe des généra-
teurs électriques.
On modélise par une résistance Rla résistance du circuit et on ori-
ente le sens conventionnel du courant de manière arbitraire. On note
−→
vla vitesse de translation de la barre [CD]. Le champ magnétique
−→
Best vertical et uniforme.
On négligera l’inductance propre du circuit.
R
A
iC
D
−→
v
l
x
0x(t)
−→
B=B−→ ez
−→
ez
−→
ey
−→
ex
(1) Si la barre est en mouvement dans le sens indiqué par le schéma, expliquer l’existence puis prévoir sans calculs le signe du courant
i.
(2) Après avoir calculé le flux à travers le circuit, tracer un schéma électrique équivalent et écrire l’équation électrique du circuit.
(3) Après avoir effectué un bilan des forces sur un système judicieux, déterminer l’équation mécanique du système.
(4) Les deux équations sont couplées. En utilisant les deux équations, en déduire une équation ne portant que sur la vitesse vde la
barre (aucune mention de i). En déduire les valeurs limites de la vitesse vlim et du courant ilim.
(5) Résoudre cette équation en supposant que la force exercée par l’opérateur est constante et que la barre est immobile à t=0. En
déduire i(t).
(6) Réaliser un bilan de puissance électrique à partir de l’équation électrique.
(7) Réaliser un bilan de puissance mécanique à partir de l’équation mécanique.
(8) Quel lien remarquez-vous entre la puissance électrique induite et la puissance de la force de Laplace? Écrire alors le bilan de
puissance global. Que devient-il en régime permanent.
Exercice 8 Rails de Laplace: MoteurExercice 8 Expliquer le fonctionnement d’un moteur à entrefer plan
Établir l’équation électrique
Établir l’équation mécanique
Faire un bilan d’énergie
On utilise à nouveau les rails de Laplace mais cette fois un généra-
teur continu impose un courant dans le circuit. On suppose que i,E
et Bsont positifs.
On notera vla projection de la vitesse −→ vsur −→ ex. On suppose
qu’initialement la vitesse de la barre est nulle.
R
E
iC
D
−→
v
l
x
0x(t)
−→
B=B−→ ez
−→
ez
−→
ey
−→
ex
(1) Expliquer qualitativement dans quel sens va bouger la barre et justifier le sens de la force électromotrice induite.
(2) Écrire l’équation électrique après avoir tracé un schéma équivalent du circuit.
(3) Écrire l’équation mécanique.
(4) Découpler les équations et déduire les valeurs limites du courant et de la vitesse de la barre.
(5) Résoudre les équations et tracer les courbes représentatives de vet i.
(6) Réaliser un bilan d’énergie. Comment peut-on améliorer la conversion de puissance électrique en puissance mécanique?
3/4

I2: Lois de l’induction Exercices de cours
Exercice 9 Haut parleurExercice 9 Expliquer le fonctionnement d’un haut parleur électrodynamique
Écrire l’équation électrique
Écrire l’équation mécanique
Faire un bilan énergétique
Les rails de LAPLACE, qui sont alimentés par un générateur de ten-
sion E, comportent une résistance Ret une auto-inductance L(pour
tenir compte du fait que les haut-parleurs réels sont bobinés).
On note −→ Ble champ magnétique uniforme vertical dans lequel
baignent les rails. La barre mobile est soumise à une force de frot-
tements de la part des rails −→ Ff=−λ−→ v(λ > 0). Comme la barre
de masse mest solidaire d’une membrane servant à transmettre la
vibration à l’air, une force de frottement supplémentaire s’applique
sur la barre −→ Fson =−α−→ v(α > 0)
Un ressort de raideur krelie la barre à un solide fixe dans le
référentiel d’étude.
R
E
L
iC
D
−→
v
l
a
x
0x(t)
−→
B=B−→ ez
−→
ez
−→
ey
−→
ex
(1) Tracer un schéma équivalent et en déduire l’équation électrique du circuit.
(2) Écrire l’équation mécanique que vérifie la position de la barre.
(3) En régime sinusoïdal forcé, le haut parleur transformera-t-il bien une tension sinusoïdale en une position de la barre sinusoïdale?
Pourquoi? Comment obtenir une bonne fidélité du haut parleur?
(4) Réaliser un bilan de puissance. Quel terme du bilan est le terme de source et quel terme est le terme utile? Comment augmenter le
rendement du haut-parleur?
4/4