PARTIE IV : La mesure du temps dans l`histoire de la Terre et de la vie.

PARTIE IV : La mesure du temps dans l’histoire de la Terre et de la vie.
Chapitre 2 : La datation absolue.
La datation absolue permet de chiffrer l’âge des roches et des fossiles et ainsi de mesurer la durée des
phénomènes géologiques en nombre d’années. Elle permet aussi de situer dans le temps l’échelle relative des
temps géologiques.
I / Le principe.
Les méthodes de radiochronologie reposent sur la présence d’atomes d’éléments radioactifs piégés dans les
roches au moment de leur formation.
Un isotope radioactif (élément père) se transforme spontanément, au cours du temps, en un isotope stable
(élément fils).
Exemples : 14C --> 14N. Elément père devient élément fils. 87Rb --> 87Sr 40K --> 40Ar
Donc au cours du temps, le nombre d’atomes de l’isotope père diminue et celui de l’isotope fils augmente.
Toutes les méthodes de datation absolue reposent sur la possibilité de mesurer, à l’aide d’un spectromètre de
masse, la richesse d’un échantillon en isotopes père restants ou isotopes fils apparus.
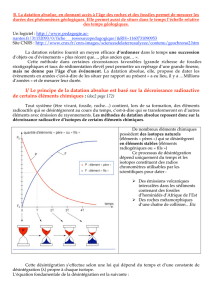
Selon la loi de radioactivité, le nombre d’atomes radioactifs décroît au cours du temps de manière
exponentielle suivant la formule :
N(t) = N(0) e-λt
où N0 = nombre d’atomes de l’élément présent au moment de la fermeture du système
Nt = nombre d’atomes restant au moment de la mesure
t = le temps écoulé
λ = constante radioactive (ou constante de désintégration) caractéristique de chaque isotope radioactif.
Elle traduit la probabilité qu’un atome de l’élément radioactif se désintègre en 1 an.
d’où l’on tire :
t = (1/λ) ln (N(0) / N(t))
Le temps t calculé correspond à la fermeture du système, c’est à dire à la cristallisation de minéraux ou à la mort
d’un organisme.
Quelle que soit la quantité d’éléments père, au départ, dans l’échantillon, il faut toujours le même temps pour que
cette quantité soit divisée par 2 : cette durée est appelée demie vie ou période. La période (T) = temps au bout
duquel la moitié des éléments radioactifs présents à un moment donné se sont désintégrés. Plus la constante de
désintégration est faible, plus la période T est longue. T = ln2 / λ d’où T = 0,693 / λ
période de 14C = 5730 ans ; période de 40K = 1250 Ma ; période de 87Rb = 48 800 Ma.
Doc.3 page 284
II / Le choix d’une méthode appropriée à l’échantillon.
Les radiochronomètres sont choisis en fonction de la période de temps que l’on cherche à explorer.
Il faut prendre en compte la période (ou demi-vie) de l’élément radioactif.
Par exemple, la méthode au 14C ne peut guère être utilisée au-delà de 40 000 ans car au-delà, il ne resterait
pratiquement plus d’isotope radioactif.
1) Le 14C, un géochronomètre limité au Quaternaire récent.
Le 14C est radioactif et se désintègre en 14N avec une période de 5730 ans. En raison d’un équilibre
permanent entre sa synthèse dans la haute atmosphère et sa décroissance radioactive, la quantité de 14C présent
dans l’atmosphère est constante (rapport 14C/12C constant et n’a pas changé durant les 50000 dernières années).
Ces isotopes sont intégrés dans des molécules du CO2 atmosphérique et, via la photosynthèse et les chaînes
alimentaires, se retrouvent dans les molécules organiques des êtres vivants ou les molécules minérales qu’ils
élaborent (carbonates des coquilles). On admet que durant la vie d’un organisme, le rapport 14C/12C de ses
molécules est constant et égal à celui de l’atmosphère.

A la mort de l’organisme, le 14C ne peut plus être renouvelé. Sans échanges avec l’extérieur, on dit que le
système est clos (ou fermé). La quantité de 14C y décroît selon l’équation : 14C(t) = 14C(0) e-λt et t permet alors de
dater la fermeture du système, c’est-à-dire la mort de l’organisme à l’origine de la roche sédimentaire.
On admet que le rapport isotopique 14C/12C actuel de l’atmosphère n’a pas changé depuis 50000 ans et qu’il est
donc identique au rapport initial de l’échantillon.
Connaissant ce rapport initial, on mesure le rapport 14C/12C actuel dans le fossile et on en déduit le temps :
(14C/12C)(t) = (14C/12C)(0) e-λt.
Ce qui donne t = (ln (14C/12C)(o) – ln (14C/12C)(t)) / λ
L’âge calculé correspond à la fermeture du système, donc à la mort de l’organisme.
Moins il reste de 14C dans un échantillon à dater et plus sa mort est ancienne.
Le carbone 14, du fait de sa demi-vie de 5730 ans est particulièrement bien adapté à la mesure de durées de
l’ordre de quelques dizaines de milliers d’années au plus.
Au-delà de 40 000 ans, la quantité de 14 C restante dans l’échantillon est insuffisante pour permettre une mesure
fiable.
2) Des géochronomètres des temps anciens : 40K-40Ar et 87Rb-87Sr.
◙ La méthode potassium-argon 40K devient 40Ar (et 40Ca)
Méthode très utilisée pour la datation des roches volcaniques.
Dans ce cas, on ne connaît pas la quantité de 40K piégés au départ dans les minéraux. Donc on fait
intervenir l’élément fils 40Ar, dans la formule.
Ar(t) = Ar(0) + ( K(o) – K(t) )
Or K(0) est inconnu et K(t) = K(0) x e-λt donc K(0) = K(t) x eλt.
D’où Ar(t) = Ar(0) + ( K(t) x eλt- K(t) )
Cela donne Ar(t) = Ar(0) + K(t) (eλt-1)
Comme la proportion d’atomes 40K qui se désintègre en 40Ar est de 10,5% (le reste, 80,5%, se désintègre en 40Ca),
la formule à appliquer est : Ar(t) = Ar(0) + 0,105 x K(t) x (eλt-1) or eλt-1 = λt
ce qui donne approximativement Ar(t) = Ar(0) + 0,105 x K(t) x λt
La quantité initiale d’argon lors de la fermeture du système est négligeable (l’argon étant un gaz, on estimera
qu’au moment de la fermeture du système tout l’argon s’est dissipé dans l’atmosphère) donc Ar(0) = 0.
d’où t = Ar(t) / (0,105 x K(t) x λ)
◙ La méthode rubidium-strontium. 87Rb devient 87SR
Méthode très utilisée pour la datation des granites.
Dans ce cas, on ignore la quantité de 87Rb piégée initialement, et du 87Sr est aussi piégé dans les roches au
moment de leur formation. Donc la quantité d’atomes de 87Sr qu’on mesure dans un échantillon est la somme du
87Sr présent au moment de la formation de la roche et du 87Sr provenant de la désintégration du 87Rb.
Pour dater, on fait donc intervenir un isotope stable : 86Sr et il faut faire intervenir plusieurs minéraux.
Les deux isotopes 86Sr et 87Sr ont le même comportement, de sorte que le rapport 87Sr/86Sr était exactement le
même dans tous les minéraux ayant incorporé du strontium.
En revanche, selon les minéraux, ils ont incorporé plus ou moins de Rubidium, donc les teneurs en 87Rb étaient
différentes (rapports 87Rb/86Sr différents).
Au fil du temps, tous les minéraux vont s’enrichir en 87Sr par désintégration du 87Rb. Pour chaque minéral, le
rapport 87Sr/86Sr va augmenter alors que le rapport 87Rb/86Sr va diminuer. Cette variation est d’autant plus
grande que le minéral était riche en 87Rb et que le temps écoulé est grand.
Dans l’échantillon, on dose 87Rb restant et 87Sr apparu par rapport à un élément stable 86Sr et on applique
la formule suivante : y = ax + b
L’équation est celle d’une droite dite isochrone dont la pente (a) donne l’âge de l’échantillon.
(87Sr/86Sr)(t) = (87Sr/86Sr)(0) + (87Rb/86Sr)(t) x (eλt – 1)
donc a = (eλt – 1) on peut approximativement estimer à a = λt d'où t=a/λ où a = (yb-ya) / (xb-xa)
Doc. 4 page 285
Remarques : Plus la pente est forte, plus la roche est ancienne.
Si on date une roche magmatique, l’âge calculé correspondra au moment où la roche a cristallisé.
Si on date une roche métamorphique, l’âge calculé correspondra aux phases de recristallisation et non

à l’âge de la roche.
III / Conclusion :
La chronologie absolue est fondée sur la décroissance radioactive de certains éléments chimiques : elle
exploite la relation qui existe entre rapports isotopiques et durée écoulée depuis la fermeture du système
contenant les isotopes.
Les radio-chronomètres sont choisis en fonction de la période de temps que l’on cherche à explorer.
Pour les derniers millénaires, on utilise le 14C dont la quantité lors de la fermeture du système est connue.
La mesure de la quantité de 14C restante dans l’échantillon permet de trouver un âge. Lorsque tous les éléments
radioactifs ont disparu de l’échantillon, la datation n’est plus possible.
Pour des périodes plus anciennes, on peut, par exemple, utiliser le couple potassium-argon. La quantité
initiale lors de la fermeture du système est négligeable. L’isotope de l’argon existe en quantité non négligeable
dans l’atmosphère et les fluides circulants, l’échantillon daté peut être contaminé et conduire à des dates
erronées. La contamination par l’argon de l’atmosphère rend difficile la détection de l’argon issu de la
désintégration du potassium avant que la roche ait atteint un certain âge.
On utilise aussi le couple rubidium-strontium. Dans ce cas, les quantités initiales des éléments et le
moment de la fermeture du système sont inconnus (le problème de datation renferme alors 2 inconnues). Pour
trouver l’âge d’une roche, il est donc nécessaire de disposer d’au moins 2 équations et donc de mesurer les
rapports isotopiques de plusieurs minéraux de la même roche ayant cristallisé au même moment.