vitesse mécanique système

Volume 48, Number 1, 2007 3
Commande Non Linéaire d’une
Machine Asynchrone sans Capteur
Mécanique avec Observateur du Flux
Rotorique par Mode Glissant
Abdelrahim BENTAALLAH, Abdelkader MEROUFEL,
Ahmed MASSOUM, Abdelber BENDAOUD et Karim MEDLES
Résumé — Cet article présente le concept général de la commande non linéaire de la machine
asynchrone avec observateur par mode glissant de flux rotorique et estimateur de vitesse. Le découplage
entre le flux et la vitesse est réalisé par la technique de linéarisation entrée/sortie. Le flux rotorique est
estimé par observateur par mode glissant et mis en contre réaction pour la régulation. Le capteur
mécanique est remplacé par un estimateur de vitesse puis introduit dans la boucle de régulation.
Plusieurs essais de simulation sous Simulink/Matlab sont effectués en vue de mettre en évidence les
performances du système de commande.
Mots clés — Commande non linéaire, linéarisation, observateur, mode glissant.
1. Introduction
Les observateurs non linéaires ne sont
pas très développés devant les observateurs
linéaires. Cependant, les chercheurs s’étaient
intéressés à développer des observateurs pour
les systèmes ayant une non linéarité régulière
comme le système des flux rotorique et
statorique au sein de la machine asynchrone
[1,2,3]
Grâce aux propriétés importantes des
systèmes à structure variable, les chercheurs
ont pensé aux observateurs basés sur
l’approche du mode de glissement. Ces
observateurs ont la même structure que les
observateurs classiques [6,7,8].
La différence réside dans la contre
réaction qui dépend d’une fonction ‘sign’.
Dans cet article, on a opté pour
l’observateur de flux à mode glissant, qui
présente une contre réaction robuste. D’autre
part, pour une simplicité de commande non
linéaire avec observateur du flux à mode
glissant, on a préféré l’utilisation d’un
estimateur de vitesse en vue d’éliminer le
capteur mécanique et de réduire
l’encombrement de la machine. Cette
structure de commande non linéaire
simplifiée, présente de bonnes performances
avec les régulateurs classiques.
2. Modèle non linéaire de la MAS
alimentée en tension
Le modèle de la machine dans le
référentiel d-q choisi de telle manière que le
flux rotorique possède une composante nulle
selon l’axe q est donné par les équations
d’états suivantes :
U.G)X(FX +=
 (1)
Avec :
)xxxx()ii(X 4321
T
qsdsqsds ==
ΦΦ
(2)
t
4321 )),x(f),x(f),x(f),x(f()x(F = (3)

ACTA ELECTROTEHNICA 4
J
C
xx.
L
M
J
1
)x(f
x.
L
R
x.M
L
R
)x(f
u.
L.
1
xx
x
xx
R
L
M
x.x
LL.
M
x).
L.
R
L
M
L.
R
()x(f
u.
L.
1
xx
x
x
R
L
M
x.R
L
M
L.
1
x).
L.
R
L
M
L.
R
()x(f
r
32
r
4
3
r
r
1
r
r
3
qs
s
41
3
21
r
r
43
rS
2
s
r
2
r
2
s
s
2
ds
s
42
3
2
2
r
r
3r
2
r
S
1
s
r
2
r
2
s
s
1
−=
−=
++−−+−=
+++++−=
σσσσ
σσσσ
(4)
Où :
rs
2
L.L
M
1−=
σ
; 2
rs
2
r
s
s
L.L.
MR
L.
R
σσ
λ
= ;
[]
t
s1 000L.1)x(g
σ =
[
t
s2 00L.10)x(g
σ =
]
(5)
t
sqsd )UU(U = (6)
2.1.Choix des sorties
Le choix des sorties est lié aux objectifs de
commande, on choisit comme sortie x3
(composante du flux rotorique selon l’axe d)
et x4 (la vitesse) [4,5] ; on pose :
⎥
⎦
⎤
⎢
⎣
⎡
=
⎥
⎦
⎤
⎢
⎣
⎡
=
4
3
2
1
x
x
)x(h
)x(h
)x(Y (7)
2.2.Linéarisation entrée/sortie
La condition permettant de vérifier si le
système non linéaire admet une linéarisation
E/S est la détermination du degré relatif.
a) Degré relatif à la sortie
)x(Y1
u).x(hLL)x(hL)x(h)x(Y
)x(h.L)x(h)x(Y
1fg1
2
f11
1f11
+==
==
(8)
Le degré relatif associé à est r1=2
)x(Y1
b) Degré relatif à la sortie
)x(Y2
u).x(hL.L)x(h.L)x(h)x(Y
)x(h.L)x(h)x(Y
2fg2
2
f22
2f22
+==
==
(9)
Le degré relatif associé à est r2=2
)x(Y2
Avec :
()
()
)x(fx)x(fx
JL
M
)x(hL
)x(f)x(Mf
L
R
)x(hL
3223
r
2
2
f
21
r
r
1
2
f
+=
−=
(10)
Le choix de ces sorties aboutit à une
linéarisation complète d’ordre 4 (r1+r2=n= 4)
avec n : ordre du système.
2.3. Transformation difféomorphisme
Le changement de coordonnées non
linéaire nécessaire est donné par le système
d’équations suivant [3,4,5].
)x(f)x(hLz
x)x(hz
)x(f)x(hLz
x)x(hz
42f4
423
31f2
311
==
==
==
=
=
(11)
L’application du changement de
variables (11) au système d’équations (4)
aboutit à l’écriture suivante :
222fg2
2
f4
43
111fg1
2
f2
21
vu)x(hLL)x(hLz
zz
vu)x(hLL)x(hLz
zz
=+=
=
=+=
=
(12)
2.4. Loi de commande non linéaire
Pour avoir une linéarisation E/S
complète d’ordre 4 en boucle fermée, il faut
appliquer le retour d’état non linéaire, à
condition que 0)0(
r
≠
Φ
:
(
)
[
]
)x(Avv)x(DU t
21
1−= − (13)
Où
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
rs
3
rs
r
LLJ
Mx
0
0
LL
MR
)x(D
σ
σ
(14)
est la matrice de découplage, avec :
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
=)x(hL
)x(hL
)x(A
2
2
f
1
2
f (15)

Volume 48, Number 1, 2007 5
L’application de la loi (13) au système
d’équation (12) aboutit au modèle linéaire
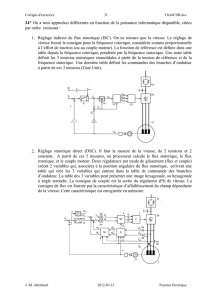
(16) schématisé par la figure 1.
21 zz =
12 vz =
(16)
43 zz =
24 vz =
3. Commande par imposition de
trajectoire
Pour poursuivre des trajectoires de
référence du flux ( Z1ref) et de vitesse ( Z3ref)
avec une certaine dynamique, on impose au
système linéarisé des pôles stables répondant
aux performances désirées (polynôme
d’Hurwitz). Les entrées v1, v2 peuvent être
calculées de la façon suivante :
(
)
(
)
()()
ref33ref3222ref3212
ref1ref1121ref1111
zzzkzzkv
zzzkzzkv
+−+−=
+−+−= (17)
Les équations d’erreur de poursuite
deviennent :
0ekeke
0ekeke
2212222
1111121
=++
=
++
(18)
Avec :
1ref11 zze −=
3ref32 zze −=
Les coefficients Kij (i = 1,2 ; j = 1,2)
sont choisis de manière à satisfaire le
polynôme d’Hurwitz.
0sskk 2
1211 =++
(19) 0ss.kk 2
2221 =++
Comme le flux est difficilement
accessible, il est préférable de l’estimer par
un observateur en vue de le contrôler par un
régulateur classique.
4. Structure générale d’un observateur
par mode glissant
Considérons le système non linéaire
suivant :
),,( tuxfx
=
 (20)
2
z
=
Considérons aussi le vecteur y des
variables mesurables qui sont reliées
linéairement avec les variables d’état ; [6,7,8]
Cxy
=
(21)
Si le système est observable, l’objectif
de l’observateur est de donner la meilleure
estimation des variables d’état à partir des
mesures sur la sortie y et sur l’entrée u.
Nous définissons l’observateur par la
structure suivante [8,9] :
s
utuyxfx Λ+= ),,,
ˆ
(
ˆ
 (22)
Avec :
est de même dimension que
x
ˆ)(nx
f
ˆ
est le modèle d’estimation
Λ
est la matrice des gains de dimension
n×r (r est la dimension de u)
est un vecteur définit par :
s
u
[
]
t
r21s )s(sign)s(sign)s(signu …= (23)
[
][
x
ˆ
CySsss t
r2 −==
Γ …
]
(24)
Γ
est une matrice carrée (r x r) à
déterminer.
d’erreur
Nous définissons aussi le vecteur
ˆ
exx
=
− en soustrayant les
équations (21) et (19), ensuite nous
obtenons :
s
ufe
Λ
Δ
−
=
 (25)
Avec
)t,u,y,x
ˆ
(f)t,u,x(ff −
=
Δ
Le vecteur surface S=0 est attractif, si :
ii SS  < 0 pour i= 1, r (26)
Durant le mode de glissement, le terme
de commutation (22) est nul. Car le vecteur
surface et sa dérivée sont nuls ( ).
0SS ≡≡ 
1
z
v=
2
z
v=4
z=
11
1
z=
x
3
z=
x
11
Fig. 1. Système découplé et linéaire.

ACTA ELECTROTEHNICA 6
La grandeur équivalente du terme de
commutation est donnée comme suit :
0)
~
(=Λ−ΔΓ s ufC (27)
Donc, on peut écrire :
fCCusΔΓΛΓ= −1 )(
~
(28)
La matrice doit être inversible.
Cela constitue la première exigence sur le
choix de et Γ. La dynamique de l’erreur
est gouvernée par l’équation (29).
ΛΓC
Λ
fCCIe ΔΓΛΓΛ−= −))(( 1
 (29)
Le choix des matrices et et le
modèle est donc décisif pour assurer la
convergence de l’erreur vers zéro.
ΓΛ
f
ˆ
5. Observateur par mode de glissement
(MG) du flux rotorique
L’objectif est d’estimer les composantes
du flux rotorique ),( qrdr
Φ
Φ
à base des
courants et des tensions statoriques qui sont
facilement mesurables.
Le vecteur sortie utilisé pour
l’estimation est donné par :
x
00010
00001
xCy ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
== (30)
Considérons maintenant le système du
moteur asynchrone en tenant compte des
variables ids, iqs, Фdr, Фqr. ; les variables à
observer sont donc :
qrdrqsds ˆ
,
ˆ
,i
ˆ
,i
ˆ
ΦΦ
Le système à observer est :
11
11
1
1
ds ds s qs dr r qr ds
rs
qs s ds qs r dr qr qs
rs
dr ds dr sl qr
rr
qr qs sl dr qr
rr
iiik k
TL
iii kk
TL
Mi
TT
Mi
TT
λω ω σ
ωλω σ
ω
ω
⎧=− + + Φ+ Φ+
⎪
⎪
⎪=− − − Φ + Φ +
⎪
⎪
⎨
⎪Φ= − Φ+ Φ
⎪
⎪
⎪Φ= − Φ− Φ
⎪
⎩
v
v
(31)
Le modèle de l’observateur est :
1
1
2
1
1
2
2
2
11
ˆˆ
ˆ
11
ˆˆ
ˆ
1
ˆˆˆ
1
ˆˆˆ
ds ds s qs dr r qr ds s
rs
qs s ds qs r dr qr qs s
rs
dr ds dr sl qr s
rr
qr qs sl dr qr s
rr
iiik k v
TL
iii kk v
TL
Miu
TT
Miu
TT
λω ω σ
ωλω σ
ω
ω
⎧=− + + Φ+ Φ+ +Λ
⎪
⎪
⎪=− − − Φ + Φ + +Λ
⎪
⎪
⎨
⎪Φ= − Φ+ Φ+Λ
⎪
⎪
⎪Φ= − Φ− Φ+Λ
⎪
⎩
u
u
(32)
Fig. 2. Schéma de principe d’un observateur par
mode glissant. Mode de glissant.
Nous définissons la matrice des gains
comme suit :
[
]
21
j
i
ΛΛΛ = pour i = 1,2 et j = 1,2
Avec :
,
⎥
⎦
⎤
⎢
⎣
⎡
=2
1
1
1
1
Λ
Λ
Λ
⎥
⎦
⎤
⎢
⎣
⎡
=2
2
1
2
2
Λ
Λ
Λ
Pour avoir l’erreur d’observation, nous
soustrayons (31) de (32), ce qui donne :
2
1
1
1
1
2
2
2
1
1
1
1
qs r dr qr s
r
ds dr r qr s
r
dr dr sl qr s
r
qr sl dr qr s
r
ikk
T
ik k u
T
u
T
u
T
ω
ω
ω
ω
⎧=− Φ + Φ −Λ
⎪
⎪
⎪=Φ+Φ−Λ
⎪
⎪
⎨
⎪Φ=− Φ+ Φ−Λ
⎪
⎪
⎪Φ=− Φ− Φ−Λ
⎪
⎩
u
(33)
Avec
[
]
t
21s )s(sign)s(signu =
et .
()
y
ˆ
y
s
s
S
2
1−=
⎥
⎦
⎤
⎢
⎣
⎡
= Γ
Le vecteur d’erreur est :
[]
rS
Ie Φ =
Posons les représentations matricielles
suivantes :
[
]
10C
=
,

Volume 48, Number 1, 2007 7
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−
=
r
r
r
r
1
T
1
kk
k
T
1
k
A
ω
ω
,
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
−−
−
=
r
sl
sl
r
2
T
1
T
1
A
ω
ω
Le système (31) devient :
1
11
1
22
s
r
rs
s
I
Au
A
u
⎧=Φ−Λ
⎪
⎨Φ= Φ −Λ
⎪
⎩
 (34)
La surface y)y
ˆ
y(S Γ
Γ
=−= ,
d’où
s
IS Γ = (35)
La fonction de
Lyapunov est : [9,10,11]
SS
2
1
Vt = > 0 (36)
d’où la dérivée
,V
s
tISV 
Γ = (37)
Notons que dtd
Γ
doit être nulle.
Après un calcul intermédiaire, nous
obtenons :
s
1
1
t
r1
tuSASV
ΛΓΦΓ −=
 (38)
En posant , il suffit de
vérifier la condition (37) pour satisfaire la
condition d’attractivité des surfaces.
⎥
⎦
⎤
⎢
⎣
⎡
=
2
1
10
0
δ
δ
ΛΓ
r1
t
2211 ASSS
ΦΓδδ >+ (39)
La détermination des gains se fait selon
deux étapes :
- La première consiste à satisfaire la
condition d’attractivité :
⎥
⎦
⎤
⎢
⎣
⎡
=−
2
1
1
10
0
δ
δ
ΓΛ
(40)
- La deuxième consiste à imposer pour
l’erreur une dynamique de convergence
exponentielle.
Lorsque le régime de glissement est
établit ( 0Is=
 et 0I s=), nous avons alors :
r1
1
1s
u
~
ΦΛΛ
−
= (41)
Par substitution, l’erreur sur r
Φ
devient :
(
)
r1
1
122r AA
ΦΛΛΦ
−
+−−=
 (42)
Pour que l’erreur converge
exponentiellement, nous devons poser :
rr Q
ΦΦ −=
 (43)
Avec , , sont des
constantes positives
⎥
⎦
⎤
⎢
⎣
⎡
=
2
1
q0
0q
Q1
q2
q
D’où :
⎥
⎦
⎤
⎢
⎣
⎡
+= −−
2
1
11
122 0
0
)AQ(
δ
δ
ΓΛΛ
(44)
Pour une raison de simplification, nous
posons :
1
1
−
= ΛΓ (45)
La condition 0dtd =Γ est vérifiée en
considérant que la vitesse est suffisamment
lente devant la dynamique de l’observateur.
Ce qui en résulte :
⎥
⎦
⎤
⎢
⎣
⎡
=
2
1
11 0
0
A
δ
δ
Λ
(46)
⎥
⎦
⎤
⎢
⎣
⎡
−=
2
1
22 0
0
)AQ(
δ
δ
Λ
(47)
Par développement, nous obtenons :
()
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡−
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=
r
r
r
r
2
r
2
r
T
1
kk
k
T
1
k
k
T
1
k
1
ω
ω
ω
Γ
(48)
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
r
2r2
r1
r
1
1
T
1
kk
k
T
1
k
δωδ
ωδδ
Λ
(49)
⎥
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎢
⎣
⎡
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−−
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−
=
r
22sl2
sl1
r
1
2
T
1
q
T
1
q
δωδ
ωδδ
Λ
(50)
Ainsi, la condition d’attractivité devient
comme suit :
rSSS t
2211
Φδδ >+ (51)