4e – Fiche de référence Géométrie 1 – Les quadrilatères

4
e
– Fiche de référence Géométrie 1 – Les quadrilatères
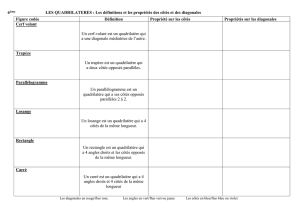
Un quadrilatère est une figure plane à quatre côtés.
Il existe des quadrilatères croisés et des quadrilatères non croisés.
Trapèzes
Un quadrilatère non croisé qui possède deux côtés opposés parallèles s’appelle
un trapèze.
Pour justifier qu’un quadrilatère est un trapèze, il suffit de prouver qu’il possède deux côtés
opposés qui sont parallèles.
Trapèzes particuliers
Parallélogrammes
Un quadrilatère dont les côtés opposés sont parallèles s’appelle un parallélogramme.
Pour justifier qu’un quadrilatère est un parallélogramme, il suffit de prouver que tous ses côtés
opposés sont parallèles.
Propriété caractéristique des parallélogrammes
• Les diagonales d’un parallélogramme se coupent en leur milieu.
On a donc deux façons différentes de prouver qu’un quadrilatère est un parallélogramme.
 On prouve que ses côtés opposés sont tous parallèles.
OU  On prouve que ses diagonales se coupent en leur milieu
Q
uadrilatère
croisé
Q
uadrilatère
non
croisé
Exemples de trapèzes
Trapèze isocèle
Trapèze
rectangle

Autres propriétés des parallélogrammes
• Les côtés opposés d’un parallélogramme ont la même longueur
• Les angles opposés d’un parallélogramme ont la même mesure.
Rectangles
Un quadrilatère dont les quatre angles sont droits s’appelle un rectangle.
Un rectangle est un parallélogramme particulier, donc il possède toutes les propriétés des
parallélogrammes énoncées plus haut.
Il possède une propriété importante supplémentaire :
• Les diagonales d’un rectangle ont la même longueur.
Comment démontrer qu’un quadrilatère est un rectangle ?
 On démontre qu’il a trois angles droits (le 4
e
angle est alors forcément droit).
OU  On démontre que c’est un parallélogramme, puis qu’il a un angle droit.
OU  On démontre que c’est un parallélogramme, puis que ses diagonales ont la
même longueur.
Losanges
Un quadrilatère dont les quatre côtés ont la même longueur s’appelle un losange.
Un losange est un parallélogramme particulier, donc il possède toutes les propriétés des
parallélogrammes énoncées plus haut.
Il possède une propriété supplémentaire :
• Les diagonales d’un losange sont perpendiculaires.
Comment démontrer qu’un quadrilatère est un losange ?
 On démontre qu’il a quatre côtés de même longueur
OU  On démontre que c’est un parallélogramme, puis qu’il a deux côtés
consécutifs de même longueur.
OU  On démontre que c’est un parallélogramme, puis que ses diagonales sont
perpendiculaires.
Carrés
Un quadrilatère qui est à la fois un rectangle et un losange s’appelle un carré.
Pour démontrer qu’un quadrilatère est un carré, on démontre que c’est à la
fois un rectangle et un losange en utilisant les propriétés ci-dessus.