Vitesse Force qui relentit Vitesse Force qui tourne

SCA 3630 Labo de Météo I Vents-1 Vent, pression et Coriolis
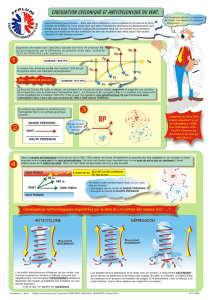
Les vents, gradients de pression et Coriolis
La vitesse, l'accélération et les forces
La deuxième loi de Newton nous informe que tout objet garde sa vitesse (y compris sa direction)
constante, par rapport aux étoiles fixes, à moins qu'une force nette agisse sur lui. (Étoiles fixes: à
cause de la grande distance qui nous sépare des étoiles autres que le Soleil, elles ressemblent à des
points qui maintiennent leurs distances mutuelles. Elles semblent immobiles. C'est pourquoi on les
choisit comme un repère privilégié pour l'étude des mouvements). Pour une force donnée, le
changement de vitesse dépend de la masse de l'objet. Plus grande est la masse de l'objet, plus petit
est le changement de vitesse provoqué par l'action de la force. Par exemple, il est plus difficile de
changer la vitesse d'un gros joueur de hockey que celle d'un petit.
Vitesse
Force qui relentit
Vitesse
Force qui tourne
Figure 6-1: Forces et vitesse
Lorsque nous sommes assis sur notre chaise, nous tournons avec la Terre. Donc, par rapport aux
étoiles fixes, nous avons une vitesse de déplacement qui change toujours de direction. Il y a donc
une accélération (changement de grandeur ou direction de la vitesse). Les parcelles d'air au-dessus
de notre tête dans la salle de classe tournent aussi avec la Terre. L'air, dehors, même lorsqu'on ne
perçoit pas de mouvement, tourne aussi avec la Terre. Notre vitesse est toujours en train de changer
de direction (il y a donc une accélération). Il doit donc y avoir une force qui provoque ce
changement. En effet, une faible partie de la force de gravité est la responsable de cette modification
de la direction de notre vitesse. C'est la même chose pour une balle au bout d'une ficelle. Il faut tirer
sur la ficelle (exercer une force) pour que la balle tourne autour de nous. Nous ne sentons pas cette
variation de vitesse parce que le taux de changement est très petit. Nous ne voyons pas l'air (il n'y a
pas de vent) se déplacer ni changer de direction parce nous tournons aussi avec la Terre (notre
vitesse est exactement la même que celle de l'air que nous pensons être au repos).

SCA 3630 Labo de Météo I Vents-2 Vent, pression et Coriolis
Force de
gravité
Vitesse du
professeur
Rotation
Figure 6-2: Professeur tourne avec la Terre. La force de gravite change
sa vitesse
Les vents à la petite échelle (sans l'effet de la rotation de la Terre)
Nous avons appris que la pression au sol est égale au poids de l'air dans la colonne au-dessus d'une
surface unitaire. En effet, la pression à n'importe quel niveau égale le poids de l'air, par unité de
surface, au-dessus de ce niveau.
Figure 6-3: Force exercée par unité d’aire sur une surface par le poids de
l’air au-dessus

SCA 3630 Labo de Météo I Vents-3 Vent, pression et Coriolis
Figure 6-4: Pression de surface. Pression en un point qui se trouve sur
la surface de la terre.
Cela veut dire que nous pouvons avoir une haute pression ou une basse pression (dépression,
cyclone, perturbation, creux, etc.) avec des températures chaudes ou froides au sol parce que la
pression au sol dépend du poids total de l'air au-dessus et non de la température locale de l'air.
Figure 6-5: Pression à un niveau donné égale le poids de l'air au-dessus
S'il existe une différence de pression entre 2 points sur un plan horizontal, qu'on appelle un
gradient horizontal de pression, cette différence produit une force de gradient de pression qui agit
sur les parcelles d'air entre ces deux points. Cette force se dirige de l'endroit de plus haute pression
vers l'endroit de plus faible pression.

SCA 3630 Labo de Météo I Vents-4 Vent, pression et Coriolis
Figure 6-6: Force de gradient de pression
Figure 6-7: Carte avec isobares et la force horizontale de gradient de
pression.
Brise locale: pas d'effet de la rotation de la Terre
Nous verrons plus loin que l'effet de rotation de la Terre (effet de Coriolis) a un impact sur les vents
seulement lorsque les distances parcourues sont grandes. Dans les cas de vents locaux comme les
brises de mer et de terre, les vents de vallée, etc., les distances sont trop petites pour que l'effet de
Coriolis soit important.
Formation de brise de mer

SCA 3630 Labo de Météo I Vents-5 Vent, pression et Coriolis
Dans les journées chaudes et ensoleillées d'été, au bord de la mer, on observe le développement d'un
vent qui souffle de la mer vers la terre. Parce que l'air au-dessus la mer est plus frais que l'air au-
dessus de la terre, cette brise (de mer) rafraîchit la côte. Sa formation est assez simple à comprendre.
Supposez que le matin il n'a pas de différence de température entre l'air au-dessus de la terre et de la
mer (pas de gradient horizontal de la température) et que la pression ne varie pas non plus sur le
plan horizontal (pas de gradient horizontal de la pression). Le soleil commence à briller.
Terre Mer
1000 hPa
900 hPa
800 hPa
700 hPa
Hauteur
20˚C
15˚C
10˚C
20˚C
15˚C
10˚C
20˚C
Rayons du soleil
Figure 6-8: Le matin sans gradient horizontal de température ni de
pression. Le soleil commence à briller
Une bonne partie des rayons du soleil est absorbée par la couche mince à la surface de la terre qui
se réchauffe rapidement. Le sol commence à réchauffer l'air au-dessus qui devient instable créant
des courants ascendants (thermales). L'air au-dessus de la terre devient de plus en plus chaud. Sur
la mer, la température ne change pas beaucoup parce que les rayons pénètrent dans l'eau. Ils
réchauffent un grand volume de celle-ci. De plus, il faut plus de chaleur pour réchauffer un gramme
d'eau qu'un gramme de sol (surtout sec) parce que la capacité calorifique de l'eau est beaucoup plus
grande que celle du sol. La mer ne change donc pas de température (ou très peu) et ne peut pas
chauffer l'air au-dessus. Ainsi, il s'établit une différence de température (à la même pression) entre
l'air au-dessus le terre et celle au-dessus la mer. Selon la loi des gaz parfaits, à la même pression,
l'air plus chaud est moins dense que l'air plus froid et, par conséquent, occupe un plus grand
volume.
Terre Mer
1000 hPa
900 hPa
800 hPa
700 hPa
Hauteur
25˚C
15˚C
10˚C
20˚C
15˚C
10˚C
20˚C
900 hPa
800 hPa
700 hPa
875
825
925
775
725 675
Force de gradient
horizontal de pression
Figure 6-9: Gradient horizontal de pression produit par le gradient
horizontal de température