3. La Grandeur des Forces sur le Plan Horizontal 1 ρ ∇ p ~10 f V ~

SCA2625 Dynamique C-1
SCA 2625-Dynamique Partie C
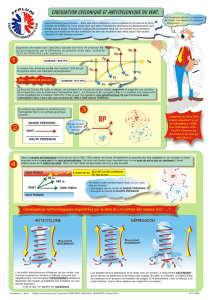
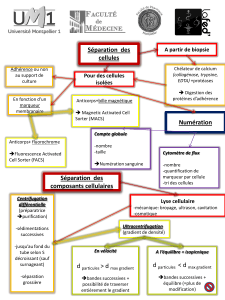
3. La Grandeur des Forces sur le Plan Horizontal
Le gradient horizontal de pression qu'on calcul sur les cartes de météo est de l'ordre de 10 hPa en
1000 km (103 hPa/106 m = 10-3 hPa/m). Avec la densité r de l'ordre de 1 Kg/m3 , la grandeur de la
force de gradient pression (par unité de masse ) est de l'ordre de
1
ρ
r
∇ p~10−3m/s2
Avec ΩT = 7,3 10-5 s-1 , le sinus des latitudes extratopicales (30 à 90) de l'ordre de 0,5 à 1, la
grandeur characteristique de f est 10-4 s-1 . Avec un vent horizontal
r
V
h
de l'ordre de 10 m/s, la force
(par unité de masse) de Coriolis est de l'ordre de
f
r
V ~10
−
3m/s2
(Dans les tropiques ces forces (par unité de masse) sont 1 ordre de grandeur plus petit.)
Par contre, l'accélération (d
r
V
h
/dt) qu'on mesure est seulement de l'ordre de 10-4 m/ s2.
En absence de l'effet de frottement, on deduit donc que sur le plan horizontal l'écoulement
répresente une quasi-équilibre (beaucoup moins bien que sur le plan vertical) entre la force de
gradient de pression et celle de Coriolis.
x,E
y,N
P0
P2
P
1ah
ph
ch
Vh - Vg
Quasi-
équilibre
Figure DynC-1: Exemple d'un quasi-équilibre sur le plan horizontal. L'accélération
r
a
h sur le
plan horizontal est un ordre de grandeur plus petit que la force (par unité de masse) de
gradient de pression
v
p
h et celle de Coriolis
r
c
h.

SCA2625 Dynamique C-2
Explication: Lorsque la différence de pression existe sur une échelle plus grande, l'effet de rotation de la
Terre (Coriolis) est aussi important que la force de gradient de pression. En absence de l'effet de
frottement si nous regardons, à partir d'une étoile fixe, une zone de gradient horizontal de pression et on
fixe notre attention sur une particule d'air, on la verra commencer à réagir à la force de gradient de
pression. La particule s'accélèrera dans la direction de cette force qui se dirige de la haute vers la basse
pression.
Haute
Pression Basse Pression
Sens de
rotation
Force de gradient
de pression
Sens de
rotation
Haute
Pression Basse
Pression
Force de gradient
de pression
Vitesse de
la parcelle
Figure DynC-2: La rotation autour de l'axe verticale locale du champ de pression pendant le
déplacement d'une parcelle d'air vers la basse pression.
Zone de haute pression
Zone de basse pression
Sens de
rotation
Zone de
haute
pression
Sens de
rotation Zone de
basse
pression

SCA2625 Dynamique C-3
Parce que la surface de la Terre est en rotation, l'axe de haute-basse pression tourne et bientôt, la
particule se trouvera en train de se déplacer entre la haute et la basse pression. La force de gradient de
pression essaiera de tourner la particule vers la basse pression. La particule tourne mais l'axe de haute-
basse pression tourne aussi approximativement au même taux. Résultat: la particule se déplace toujours
entre la haute et la basse pression avec la basse pression à sa gauche.
Si nous nous plaçons sur la Terre en tournant avec elle, nous ne voyons pas la rotation de l'axe haute-
basse pression mais il nous semble plutôt qu'une force agit sur la particule pour la tourner vers la droite
(la force de Coriolis) et qu'après une petite période d'ajustement, la particule se déplace avec une
vitesse presque parallèle aux isobares avec la basse pression à sa gauche.
source: Lutgens et Tarbuck 1986
Figure DynC-3: En absence de l'effet de frottement Les vents sont déviés par la force de
Coriolis jusqu'à ce que la force de Coriolis équilibre approximativement la force du gradient
de pression. Au-dessus d'autour de 600 mètres, là où la friction avec le sol devient
négligeable, ces vents souffleront presque parallèlement aux isobares. Avec le dos au vent,
la basse pression est à gauche.
4. Le "vent" géostrophique
Étant donné que l'accélération sur plan horizontal est un ordre de grandeur plus petit que les forces de
gradient de pression et celle de Coriolis, en absence de l'effet de frottement, nous pouvons calculer une
des forces à partir de l'autre avec une erreur de l'ordre de 10% (l'accélération qu'on néglige). En effet,
le vent hypothétique qui produirait un équilibre exact entre les deux forces s'appel le "vent
géostrophique"
r
V
g.
−1
ρ
r
∇ p=f
r
k ×
r
V g
x:
1
ρ
∂
p
∂x=fg
vC-1

SCA2625 Dynamique C-4
y:
−1
ρ
∂
p
∂y=fg
u
En effet, le vent géostrophique qu'on peut calculer à partir de ces équations est une très bonne
approximation au vent horizontal (l'erreur de de l'ordre de 10%).
−
1
fρ
r
∇ p×
r
k =
r
V g
1
fρ
∂
p
∂x=g
vC-2
−1
fρ
∂
p
∂y=g
u
Exemple du calcul approximativement au point X (pression en hPa, f=10-4s-1, ρ = 1,25 kg/m3).
∂
p
∂
x=0 donc
g
v
=
0
∂
p
∂y=1000
−
1008
(
)
×
2
10 Pa
1000 ×3
10 m= − 2
8×10 Pa
6
10 m= − −4
8×10 Pa/m
(Question: Pourquoi le numérateur est négatif pendant que le dénominateur est positif?)
Donc
g
u= − −8×
−
4
10
1,25
×
−4
10 = +6,4m/s
Donc le vent géostrophique
r
V g= +6,4
r
i +0
r
j ou 6,4 m/s vers de l'ouest vers l'est.
Xx
y1000
1004
1008
1000km

SCA2625 Dynamique C-5
500
D
504
508
Nord
Est
Force de gradient
de pression
Force de
Coriolis
Vent géostrophique Accélération
A
B
C
D
Accélération Vents
Figure DynC-4: Le vent suit les isobares: Supposons qu'au point A, le vent est
géostrophique. Donc les forces sont en équilibre exact pour la particule au point A. La
particule se déplacera donc sans accélération et ne changera pas sa vitesse. Au point B, elle
aura la même vitesse et donc la même force de Coriolis (qui dépend de la vitesse). Mais au
point B, la force de gradient de pression se dirige dans une direction différente qu'au point
A. Il n'y a plus donc d'équilibre. En effet, la somme des forces (par unité de masse),
l'accélération, est dans la direction contraire au mouvement. La vitesse de la particule
diminuera donc et la force de Coriolis deviendra plus petite que celle du gradient de
pression. La situation finale est donnée par les flèches au point C (et D) où la somme des
forces produit une accélération vers le centre de dépression qui fait tourner la particule
autour la dépression dans le sens anti-horaire (cyclonique). Notez que l'accélération reste
petite par rapport aux forces. Donc le vent géostrophique est toujours une bonne
approximation au vent.
5. Le vents d'ouests et le courant jet (Jet Stream)
Les premiers modèles de la circulation ne tenaient pas compte de la rotation de la Terre. On proposait
(Hadley) que l'air chaud des régions tropicales en altitude devrait se déplacer vers le nord et l'air froid
des régions polaires devrait aller en surface vers le sud. Donc le vent devrait aller du nord vers le sud
en surface et du sud vers le nord en altitude. Cette circulation, dite de Hadley, n'est pas observée et
on trouve que les vents en altitude sont surtout d'ouest vers l'est.
C'est encore l'effet de la rotation de la Terre qui est la cause de ce comportement. L'air plus chaud
dans les tropiques produit en altitude une force de gradient de pression du sud vers le nord (comme
pour la brise de mer) mais l'effet de Coriolis produit les vents en altitude d'ouest en est. En plus dans
les zones de forts gradients horizontaux de la température de largueur de l'ordre de 1000 km (des
fronts), l'effet de Coriolis empêche aussi des circulations convectives normales (comme la brise de