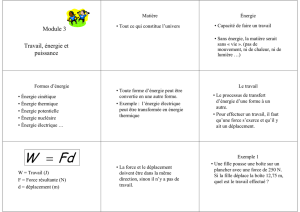
Transformation de l`énergie potentielle en

Maëla Morard 3 Novembre 2008
Gaëlle Spack
1 de 5
Transformation de l’énergie potentielle en énergie cinétique
But
Pouvoir estimer le temps que mettra la bille pour parcourir une distance
fixe connaissant la hauteur à laquelle elle est lâchée.
Résumé de l’expérience
Une bille est lâchée sur un plan incliné touchant le sol. Le point sur le sol
est à une distance constante d’un mur (voir schéma 1 ci-dessous). Afin de
pouvoir estimer le temps que mettrait la bille pour n’importe quelle
hauteur donnée du plan incliné, nous avons mesuré plusieurs temps de
parcours sur le sol en faisant varier la hauteur du plan incliné (voir tableau
1).
Schéma de l’expérience
Mur
Sol: distance fixe = 2m
Plan incliné
Temps mesuré en sec
Hauteur mesurée en m
Bille
START STOP
Mur
Sol: distance fixe = 2m
Plan incliné
Temps mesuré en sec
Hauteur mesurée en m
Bille
START STOP
Schéma 1: Présentation de l’expérience

Transformation de l’énergie potentielle en énergie cinétique
2 de 5
Tableau 1: Valeurs mesurées pendant l’expérience
*Pour le temps sur le sol, nous avons fait la moyenne de 5 mesures.
Ceci nous permet d’obtenir un résultat plus exact.
Temps en fonction de la hauteur
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
1.1
1.2
1.3
1.4
1.5
1.6
1.7
1.8
1.9
2
2.1
2.2
2.3
2.4
2.5
2.6
2.7
2.8
2.9
3
3.1
3.2
3.3
3.4
3.5
3.6
3.7
3.8
3.9
4
4.1
4.2
4.3
4.4
4.5
4.6
4.7
0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8
Hauteur [m]
Temps [sec]
Graphique 1 : Temps en fonction de la hauteur
H : hauteur
[m]
T: temps moyen
sur le sol* [sec]
V:
vitesse au sol
[m/sec]
0.62 0.956 2.092
0.47 1.006 1.988
0.41 1.178 1.698
0.74 0.876 2.283
0.31 1.206 1.658
0.76 0.916 2.183
0.14 1.716 1.166
0.26 1.292 1.548
0.57 0.964 2.075
0.05 4.382 0.456

Transformation de l’énergie potentielle en énergie cinétique
3 de 5
Hauteur en fonction de la vitesse
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
0.000 0.500 1.000 1.500 2.000 2.500
Vitesse [m/sec]
Hauteur [m]
Graphique 2 : Hauteur en fonction de la vitesse
Estimation des fonctions mathématiques avec Excel
Avec l’aide du logiciel Excel qui nous a permis de tracer les graphiques,
nous avons pu obtenir une estimation de la fonction qui relie le temps à la
hauteur du plan incliné :
55.0
7.0
−
=XY
Y= Temps [sec]
X= Hauteur [m]
Nous avons aussi obtenu la fonction qui relie la hauteur du plan incliné à
la vitesse :
139.03029.02525.0
2
+−= XXY
Y= Hauteur [m]
X= Vitesse [m/sec]

Transformation de l’énergie potentielle en énergie cinétique
4 de 5
Estimation du temps sur le sol à partir d’une hauteur
donnée
Pour notre estimation finale, nous avons utilisé notre graphique
(graphique 1) et non des calculs. La raison de ce choix est que nous
n’avions pas le logiciel Excel pendant les travaux pratiques.
Nous avons estimé un temps de 1.15 [sec] pour une hauteur de 0.36
[m].
Pour vérifier ce temps estimé, nous avons levé notre plan incliné à 0.36
[m] du sol. Ensuite, nous avons procédé de la même manière que pour
notre tableau : nous avons pris 5 mesures du temps et nous en avons fait
une moyenne.
Tableau 2: Valeurs mesurées pendant l’expérience
Cette moyenne est de 1.13 [sec] pour une hauteur de 0.36 [m].
Discussion des résultats :
1) La hauteur estimée avec le graphique est très proche de celle
mesurée.
2) Une des mesures du tableau dépasse la valeur estimée : 1.19 [sec]
3) Au vu des résultats de mesure, nous pouvons dire que nos réflexes
(appuyer sur le bouton du chronomètre) pour enclencher et déclencher
le chronomètre entraînent des résultats dont les différences sont plus
grandes que celle entre la valeur estimée et la valeur moyenne.
4) Nous pouvons voir sur le graphique 2 que la hauteur et la vitesse
sont reliées par des fonctions du type x
2
. Ceci est en accord avec la
théorie de transformation de l’énergie potentielle en énergie
cinétique :
T: temps sur le sol
[sec]
1.13
1.10
1.09
1.19
1.13
Moyenne 1.13

Transformation de l’énergie potentielle en énergie cinétique
5 de 5
2
2
1mVmgh =
m= masse de l’objet [g]
g = gravité [m/sec
2
]
h = hauteur [m]
V = vitesse [m/sec]
Remarques :
Il était difficile de mesurer les hauteurs qui dépassaient de 0.70 [m] car
notre tige de métal, qui maintenait le plan incliné, était trop petite. Nous
avons donc dû mettre des dictionnaires pour avoir ces hauteurs.
Avec ce petit problème, nous avons sûrement dû manquer de précision.
Le fait de reconstruire notre montage d’une semaine à l’autre nous a fait
perdre de la précision (difficulté à maintenir exactement les mêmes
valeurs au sol).
Eléments possibles à amélorier :
Etre plus organisées dans notre travail :
-Faire directement un tableau pour nos mesures.
-Indiquer ce qu’on est en train de mesurer (quelle hauteur) pour ne pas
avoir besoin de le refaire une seconde fois.
Ne pas avoir à refaire notre montage : essayer de faire toutes les mesures
du temps en une seule fois.
Conclusion :
Les résultats obtenus pendant le travail pratique sont en accord avec la
théorie.
Nous avons pu observer la transformation de l’énérgie potentielle en
énérgie cinétique.
Ce TP nous a été très instructif et nous avons eu du plaisir à le faire.