Exercice 1 (sans calculatrice) : Un tir au canon (v .cos ).t

Exercice 1 (sans calculatrice) : Un tir au canon
La galiote était un navire de guerre qui fit son apparition à la fin du XVII
ème
siècle, sous le règne de Louis XIV. Les galiotes
possédaient de lourds canons, fixés au pont, projetant des boulets de 200 livres (environ 100 kg)
portant jusqu’à 1200 toises (environ 2400 m).
Selon la description détaillée de Renau, Inspecteur Général de la Marine, ces bâtiments sont destinés
à emporter des canons en mer. Ils sont de moyenne grandeur et à fond plat. De par leur fabrication,
l’angle de tir des canons est fixe et a pour valeur α = 45°, ce qui permet de tirer à la plus grande
distance possible.
La structure d’une galiote doit être très robuste pour résister à la réaction considérable du boulet et
leur échantillon
(1)
est ordinairement aussi fort que celui d’un vaisseau de 50 canons.
(1)
dimension et épaisseur des pièces utilisées pour la construction.
D’après le site Internet de l’Institut de Stratégie Comparée.
1. Action de la poudre de canon sur le boulet
L’éjection du boulet est provoquée par la combustion de la poudre. Une force de poussée
est donc exercée sur le boulet par l’ensemble {galiote + canon + gaz}.
Justifier l’expression soulignée dans le texte encadré ci-dessus, à l’aide d’une des trois lois
de Newton. Énoncer cette loi. (On pourra s’aider d’un schéma).
2. La trajectoire du boulet
On souhaite étudier la trajectoire du centre d’inertie G du boulet de masse m. L’étude est
faite dans le référentiel terrestre considéré comme galiléen. Le repère d’étude est (O,
i
r
,
j
ur
)
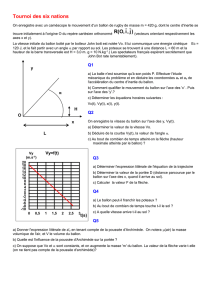
et l’origine des dates est choisie à l’instant où le boulet part du point O (voir figure 1 ci-dessous).
Le vecteur vitesse initiale
uur
du point G est incliné d’un angle α (appelé angle de tir) par rapport à l’horizontale. Une
fois le boulet lancé, la force de poussée de la partie précédente n’intervient plus.
Données :
Volume du boulet : V = 16 dm
3
= 16 L
Masse du boulet : m = 100 kg
Valeur du champ de pesanteur : g = 10 m.s
– 2
Masse volumique de l’air :
ρ
= 1,3 kg.m
– 3
2.1. Inventaire des forces agissant sur le boulet après son lancement
2.1.1. Donner l’expression littérale de la valeur F
A
de la poussée d’Archimède puis la calculer.
2.1.2. Calculer la valeur P du poids du boulet après avoir précisé son expression littérale.
2.1.3. Dans cet exercice, on pourra négliger la poussée d’Archimède devant le poids si la valeur de ce dernier est au
moins cent fois plus grande que celle de la poussée d’Archimède. Montrer que l’on est dans cette situation.
2.1.4. Pendant le vol, compte tenu de la masse, de la vitesse et de la forme du boulet, on fait l’hypothèse que les
forces de frottement dans l’air sont négligeables devant le poids. En tenant compte des résultats précédents, établir
le bilan des forces exercées sur le système {boulet} pendant le vol.
2.2. Équation de la trajectoire
Dans toute cette partie, on négligera la poussée d’Archimède ainsi que les forces de frottement dues à l’air.
2.2.1. En appliquant la deuxième loi de Newton, montrer que les équations horaires du mouvement du point G
s’écrivent : x(t) = α et y(t) = – α
2.2.2. Montrer que l’équation de la trajectoire peut se mettre sous la forme y(x) = Ax
2
+ Bx. On donnera les
expressions littérales de A et B et on précisera leurs unités respectives.
2.3. Portée du tir
L’équation de la trajectoire du boulet peut se mettre sous la forme y(x) = x ⋅ (Ax + B). Au cours d’un tir d’entraînement,
un boulet tombe dans l’eau. Dans ces conditions, la distance entre le point de départ du boulet et son point M d’impact
sur l’eau est appelée portée (voir figure 1).
On négligera la différence d’altitude entre les points O et M devant les autres distances.
2.3.1. Exprimer la portée d du tir en fonction de A et B.
Aide au calcul
1,6
×
1,3 = 2,1 ≈
2,4 1,5
1,6
= 1,2
1,3
1,3
= 0,81
1,6
4
24 ,9
≈
Figure 1
α
x
y
O
Portée d
uur
M
j
i

2.3.2. L’expression littérale de la portée d en fonction de v
0
, α et g est :
v 2
α
dg . Retrouver, en la justifiant, la
valeur α = 45° donnée dans le texte, pour laquelle la portée est maximale, pour une vitesse v
0
donnée.
2.3.3. À partir de la question précédente et des données, calculer la vitesse initiale du boulet pour atteindre la portée
maximale donnée dans le texte.
2.3.4. En fait, les frottements dans l’air ne sont pas négligeables. Avec un angle de tir restant égal à 45°, la vitesse
initiale du boulet doit-elle être supérieure ou inférieure à celle trouvée à la question 2.3.3. pour obtenir la même portée
maximale ? Justifier sans calcul.
Exercice 2 : Etude de la composition de l’atmosphère
Un ballon sonde, en caoutchouc mince très élastique, est gonflé à l'hélium. Une nacelle attachée
au ballon emporte du matériel scientifique afin d'étudier la composition de l'atmosphère.
On souhaite étudier la mécanique du vol du ballon sonde à faible altitude (sur les premières
centaines de mètres). On peut alors considérer que l'accélération de la pesanteur g, le volume du
ballon V
b
et la masse volumique ρ de l'air restent constantes.
On modélisera la valeur f de la force de frottement de l'air sur le système étudié par l'expression: f
= K. ρ .v² où K est une constante pour les altitudes considérées et v la vitesse du centre d'inertie
du système {ballon + nacelle}.
On supposera qu'il n y a pas de vent (le mouvement s'effectue dans la direction verticale) et que le volume de la
nacelle est négligeable par rapport au volume du ballon.
Le système {ballon + nacelle} est étudié dans un référentiel terrestre considéré comme galiléen.
Données : ρ
air
= 1,22 kg.m
-3
V
b
= 9,0 m
3
Masse du ballon (enveloppe + hélium) : m = 2,10 kg Masse de la nacelle vide: m' = 0,50 kg
1.1. Condition de décollage du ballon.
1.1.1 Établir le bilan des forces exercées sur le système {ballon + nacelle}, lorsque le ballon vient juste de décoller.
Indiquer le sens et la direction de chaque force.
1.1.2. Donner l'expression littérale de la valeur F
A
de la poussée d'Archimède.
1.1.3. Soit M la masse totale du système (masse du ballon, de la nacelle vide et du matériel scientifique). Appliquer
au système la seconde loi de Newton (seule la relation vectorielle est demandée).
1.1.4. La vitesse initiale du ballon (juste après le décollage) étant considérée comme nulle, à quelle condition doit
satisfaire le vecteur accélération pour que le ballon puisse s'élever ? En déduire une condition sur M (on projettera la
relation obtenue à la question 1.1.3. sur un axe vertical orienté vers le haut).
1.1.5. En déduire la masse maximale de matériel scientifique que l'on peut embarquer dans la nacelle.
1.2. Ascension du ballon.
1.2.1. À partir de la question 1.1.3. et en conservant l'axe défini à la question 1.1.4., montrer que l'équation
différentielle régissant le mouvement du ballon peut se mettre sous la forme :
A.v ² + B =
t
d
dv
et donner les expressions de A et B.
La masse de matériel embarqué étant de 2,0 kg, l'application numérique donne A= – 0,53 m
–1
et B= 13,6 m.s
–2
.
1.2.2. Une méthode de résolution numérique, la méthode d'Euler, permet de calculer de façon
approchée la vitesse instantanée du ballon à différentes dates en utilisant la relation suivante :
v(t
n+1
)= v (t
n
)+ ∆v (t
n
) avec ∆v(t
n
)= a(t
n
) . ∆t (t
n+1
= t
n
+ ∆t où ∆t est le pas de résolution)
Par cette méthode on souhaite calculer la vitesse v
1
à l'instant de date t
1
= 0,05 s et la vitesse v
2
à l'instant de date t
2
= 0,1 s, la vitesse initiale du ballon étant nulle. On prendra ∆t = 0,05 s.
En utilisant la méthode d'Euler, l'équation différentielle de la question 1.2.1 et les valeurs de A et B, recopier et
compléter le tableau suivant :
Date t
(en s)
Valeur de la vitesse v(t
n
)
(en m.s
–1
)
Valeur de l’accélération a(t
n
)
(en m.s
–2
)
∆
∆∆
∆
v(t
n
)
(en m.s
–l
)
t
0
= 0,0 0 13,6
t
1
= 0,05
t
2
= 0,10
1.3. Vitesse limite du ballon
1.3.1. Donner l'expression littérale de la vitesse limite
v
l
du ballon en fonction de A et B.
13.2. Calculer cette vitesse limite.

Corrigé de l’exercice 1 : Un tir au canon
1. Action de la poudre sur le boulet
Le système {galiote + canon + gaz} exerce une action sur le boulet : la force de poussée. Par réaction le
boulet exerce une force de recul sur le système {galiote + canon + gaz}.
La loi de Newton associée est la troisième loi : principe des actions réciproques.
Énoncé: Lorsqu'un corps A exerce sur un corps B une force
F
r
A→B
alors le corps B exerce sur le
corps A une force
F
r
B→A
telle que :
•
F
r
A→B
et
F
r
B→A
ont même droite d'action
•
F
r
A→B
= -
F
r
B→A
2. Trajectoire du boulet
2.1.1. La valeur de la poussée d'Archimède est égale au poids du fluide déplacé (ici l'air) par le boulet, soit :
F
A
= ρ.V.g
avec F
A
en N
ρ en kg.m
-3
V en m
3
(V = 16 L = 16×10
-3
m
3
)
g en m.s
-2
F
A
= 1,3 × 16×10
-3
× 10 = 1,3×1,6×10
-2
×
××
× 10 = 2,1×10
-1
= 0,21 N
2.1.2. Le poids: P = m.g
P = 100 × 10 = 1,0×
××
×10
3
N
2.1.3. Calculons
−
×
=×
A
F ,
P ,
2 1 10
1 0 10
= 2,1×
××
×10
-4
< 1,0×
××
×10
–2
donc
A
P
F
> 1,0.10
2
On peut donc bien négliger la poussée d'Archimède devant le poids.
2.1.4. Système {boulet}
Référentiel terrestre supposé galiléen
Repère (O,
i , j
r r
)
D’après 2.1.3., la poussée d’Archimède est négligeable face au poids. De plus la remarque indique
que les forces de frottement dans l’air sont négligeables devant le poids.
Le boulet n'est soumis qu'à son poids, on se place le cadre d’une chute libre.
2.2.1. La 2
nde
loi de Newton donne
P
r
= m.
a
r
⇔ m.
g
r
=m.
a
r
soit :
a
r
=
g
r
En projection selon les axes Ox et Oy du repère choisi et compte tenu du sens du vecteur
g
r
indiqué sur le schéma il vient :
x x
y y
a g
a
a g g
= =
= = −
0
r
À chaque instant :
dv
a
dt
=
r
r
donc a
x
=
x
dv (t )
dt
et a
Y
=
Y
dv (t )
dt
=
= − +
r
x
y
v (t ) Cte
v
v ( t ) g.t Cte
F
r
A→B
F
r
B→A
Corps B
Corps A

Coordonnées du vecteur vitesse initiale
v
r
:
α
α
=
=
r
x
y
v v .cos
v
v v .sin
Compte tenu du vecteur vitesse initiale
v
r
=
v( )
0
r
on a :
v
0
. cosα = Cte
1
v
0
. sinα = 0 + Cte
2
Finalement :
α
α
=
= − +
r
x
y
v (t ) v .cos
v
v (t ) g.t v .sin
À chaque instant
dOG
v
dt
=
uuur
r
donc: v
x
=
dx(t )
dt
et v
Y
=
dy(t )
dt
α
α
= +
= − + +
uuur x( t ) v .cos .t Cte
OG
y(t ) g.t² v .sin .t Cte
1
2
Or à t = 0 le projectile est au point de coordonnées (x(0) = 0; y(0) =0) donc :
0 + Cte
3
= 0
0 + 0 + Cte
4
= 0
Finalement :
x(t ) v .cos .t
OG
y(t ) g.t² v .sin .t
α
α
=
= − + 1
2
uuur
2.2.2. On tire de l'expression de x(t) = v
0
.cosα.t , le temps t que l'on reporte dans y(t) :
t = x
v .cos
α
y(x) = x² x .g. v .sin .
v .cos ² v .cos
α
α α
− +
1
2
Finalement:
2
0
1
2
x
y x g x
v
α
α
= − +
²
( ) tan
cos ²
L'expression y(x) est de la forme: y(x) = A.x² + B.x avec A qui est négatif.
Avec : A =
2
0
1 1
2gv
α
−
cos ²
B = tanα
L'unité de A est identique à celle de g / v
0
² : g s'exprime en m.s
-2
et v
0
² s'exprime en m².s
-2
donc A
s'exprime en m
-1
. B n’a pas d’unités.
2.3 Portée du tir
2.3.1 On cherche la portée du tir x
p
= d telle que: y(x
p
) = 0 ⇔ x
p
.(A.x
p
+ B) = 0
Donc: x
p
= 0 = x
O
origine du repère, la portée serait nulle, solution non retenue
Et x
p
= x
M
= d = –
B
A
2.3.2 On donne: d =
α
v .sin( )
g
2
d est maximale si sin(2α) est maximal, car v
0
et g sont constants,
soit : sin(2α) = 1 ⇔ 2α = 90° ⇔ α
αα
α = 45°.
2.3.3 on a : d =
v
g
⇔ v
0
=
d.g
Application numérique: v
0
= ,× = ×
2400 10 2 4 10
= 1,5×
××
×10
2
m.s
-1
On garde α
αα
α = 45 ° . Les forces de frottement vont s'opposer au mouvement du boulet, il faut donc une
vitesse initiale plus importante pour garder la même portée.

Corrigé de l’exercice 2 : Etude de la composition de l’atmosphère
1.1. Condition de décollage du ballon
1.1.1. Dans un référentiel terrestre (supposé Galiléen) effectuons le bilan des forces qui s’exercent sur
l’ensemble {ballon + nacelle} :
- le poids
P
r
de direction verticale et de sens vers le bas.
- La poussée d’Archimède
A
F
r
de direction verticale et de sens vers le haut
- La force de frottement de l’air f
r
de direction verticale et de sens opposé au mouvement donc vers
le bas.
1.1.2. La poussée d’Archimède est égale au poids du volume d’air déplacé : F
A
= ρ×V
b
×g
En négligeant le volume de la nacelle devant celui du ballon.
1.1.3. aMfFP
A
v
r
r
r
×=++
1.1.4. Le vecteur accélération doit être vertical et orienté vers le haut.
En projetant sur un axe vertical orienté vers le haut (Oz), il vient :
–M×g –K×ρ×v² + ρ×V
b
×g = M×a
z
(1)
Pour que le ballon décolle il suffit que a
z
> 0 soit –M×g –K×ρ×v² + ρ×V
b
×g >0
M < g
vKgV
b
2
××−×× ρρ
Juste après le décollage, la force de frottement est négligeable car la vitesse v est très faible,
alors : M <
b
V× ρ
1.1.5. Masse du système avec le matériel scientifique M' = m + m’ + m
max
Pour décoller, il faut M' < M donc M' < ρ×V
b
soit m + m' + m
max
= ρ×V
b
m
max
=
b
V× ρ – m – m’
m
max
= 1,22×9 – 2,10 – 0,50 = 8,4 kg
1.2. Ascension du ballon :
1.2.1. L’expression (1) obtenue au 1.1.4. nous donne : –M×g –K×ρ×v² + ρ×V
b
×g = M×
dt
dv
M
gMgV
v
M
K
dt
dv
b
×
−
×
×
+×
×
−
=
ρ
ρ
2
A =
M
K
ρ
×
−
B =
M
gMgV
b
×
−
×
×
ρ
1.2.2. Date t
en s
Valeur de la vitesse v(t
n
)
en m.s
-1
Valeur de l’accélération a(t
n
) en m.s
-2
∆
v(t
n
) en m.s
-
1
∆
∆∆
∆ v(t
n
) = a(t
n
). ∆
∆∆
∆ t
t
0
= 0,0 0 13,6
∆
v(t
0
) = (13,6
×
0,05)
∆ v(t
0
) = 0,68
t
1
= 0,05 v
1
= v
0
+ ∆ v(t
0
)
v
1
= 0,68
a(t
1
) = A.v
²
1
+ B
a(t
1
) = – 0,53 × (0,68)² + 13,6
a(t
1
) = 13,4
∆ v(t
1
) = a(t
1
). ∆ t
∆ v(t
1
) = 0,67
t
2
= 0,10 v
2
= v
1
+
∆
v(t
1
)
v
2
= 1,35
1.3. Vitesse limite du ballon :
1.3.1. Quand la vitesse limite est atteinte 0=
dt
dv A×v² +B = 0 v
l
=
A
B −
1.3.2. v
l
=
53,0
6,13
−
−= 5,1 m.s
-1