Étude théorique des solutions solides, leur énergie latente et

´
Etude th´eorique des solutions solides, leur ´energie
latente et constante de r´eseau
Jean Cichocki
To cite this version:
Jean Cichocki. ´
Etude th´eorique des solutions solides, leur ´energie latente et constante de
r´eseau. J. Phys. Radium, 1937, 8 (10), pp.391-396. <10.1051/jphysrad:01937008010039100>.
<jpa-00233533>
HAL Id: jpa-00233533
https://hal.archives-ouvertes.fr/jpa-00233533
Submitted on 1 Jan 1937
HAL is a multi-disciplinary open access
archive for the deposit and dissemination of sci-
entific research documents, whether they are pub-
lished or not. The documents may come from
teaching and research institutions in France or
abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est
destin´ee au d´epˆot et `a la diffusion de documents
scientifiques de niveau recherche, publi´es ou non,
´emanant des ´etablissements d’enseignement et de
recherche fran¸cais ou ´etrangers, des laboratoires
publics ou priv´es.

ÉTUDE
THÉORIQUE
DES
SOLUTIONS
SOLIDES,
LEUR
ÉNERGIE
LATENTE
ET
CONSTANTE
DE
RÉSEAU
Par
JEAN
CICHOCKI.
Institut
de
Physique
Théorique
de
l’Université
de
Poznan.
Sommaire. 2014
Nous
avons
étudié
les
solutions
solides
Cu -
Zn, 2014
Ga, 2014
Ge,
Ag 2014
Cd,
2014
In,
2014
Sn,
-
Sb
et
Cu -
Al.
Traitant
les
atomes
étrangers
substitués
dans
le
réseau
du
métal
solvent
Cu
ou
Ag
comme
centres
de
perturbation,
nous
avons
évalué
le
degré
de
cette
perturbation
à
l’aide
de
la
relation
modifiée
de
Mott -
équation
(7)
-
sur
le
potentiel
électrostatique
d’un
atome
de
valence z
+
1
en
solu-
tion
dans
un
métal
monovalent; z
étant
égal
à
1, 2, 3,....
Gràce à
cette
hypothèse
et
supposant
que
les
élec-
trons
de
valence
de
l’atome
substitué
sont
semi-libres,
modification
de
l’hypothèse
de
Mott,
nous
obtenons
l’équation
(21)
qui
nous
donne
le
volume
VS
de
l’atome
étranger
en
solution
dans
le
réseau
du
métal
sol-
vant.
Dans
les
solutions
solides
étudiées
VS
est
plus
grand
que
le
volume v0
des
atomes
du
métal
solvant
et
il
en
résulte
une
dilatation
du
réseau,
la
constante
de
réseau
dX
pour
une
concentration x
du
métal
en
solution
est
donnée
par
la
formule
(24).
L’énergie
latente
TS
est
obtenue
en
comparant
TS
au
travail
de
dilatation,
formule
(22),
et
l’abaissement
du
point
de
fusion
de
la
solution
solide
se
calcule
si
nous
admet-
tons
que
TS
est
égale
à
une
énergie
thermique
latente
de
valeur
3kT.
Le
cas
des
atomes
intersticiels
dans
les
solutions
solides
est
traité
analogiquement,
le
volume
ato-
mique
Vi
est
donné
par
l’équatton
(26).
Choisissant
comme
exemple
la
solution
solide
Cu -
Zn
nous avons
montré
qu’on
peut
négliger
les
atomes
intersticiels
par
rapport
aux
atomes
substitués,
pour
la
solution
solide
Cu -
Zn
il
y
a
à
la
température
T
=
300°
K
environ
1021
fois
plus
d’atomes
Zn
substitués
que
d’atomes
Zn
intersticiels.
1.
Introduction. -
Dans
un
travail
précédent
(1)
nous
avons
calculé
l’énergie
latente
des
solutions
solides
en
admettant
l’hypothèse
d’une
perturbation
locale
du
réseau
cristallin.
Nous
sommes
partis
de
l’hypo-
thèse
de
Mott
{~),
d’après
laquelle
un
atome
de
valence
~
-~- ~
en
solution
dans
un
métal
monovalent,
Cu,
Ag,
Au,
agit
dans
le
réseau
cristallin
comme
un
centre
de
perturbation,
ayant
par
rapport
aux
atomes
du
métal
solvant
une
charge
supplémentaire
positive
ze,
où z
est
égal
ai,
2,
3,
et
e
est
la
charge
élémentaire.
En
parti-
culier,
il
diffuserait
les
électrons
de
conduction
d’après
la
loi
de
Ruthereord
proportionnellement
au
carré
de
z,
en
accord
avec
les
expériences
de
Linde
(3)
sur
l’accrois-
sement
de
la
résistance
électrique
des
solutions
solides.
Mott(2)
a
établi
pour
le
potentiel
électrostatique 4>
(R)
dû
à
l’atome
en
solution
la
formule
R
est
la
distance
du
centre
diffuseur, q
définit
l’effet
écran
et
dépend
de
la
densité
lVo
des
électrons
libres
du
métal
solvant,
la
valeur
nuinérique
de
son
carré
est
donnée
par
Nous
avons
interprété
(i)
l’équation
(1)
en
admettant
que
grâce
à
l’introduction
de
l’atome
étranger
dans
le
réseau
du
métal
solvant
il
en
résulte
une
déformation
locale
de
réseau
dans
le
sens
de noseuhain (’),
ce
qui
se
traduit
par
une
compression
des
atomes
(entourant
l’atome
étranger
en
solution.
En
supposant,
une
densité
uniforme
de
la
négative
des
électrons
libres
il
apparaîtrait
en
conséquence
une
densité
de
charge
électrique
positive ?
(R),
fonction
de
la
distance. R
du
centre
diffuseur,
pour
laquelle
nous
avons
obtenu
(~) :
*.
La
compression
atomique
s’exprimait
alors
par
où
uo
est
le
volume
d’un
atome
du
métal
solvant.
A
Paidede
ces
relations
nous
avons
calculé
le
volunle Vs
de
l’atome
substitué
et
nous
avons
obtenu
(1) :
où
rs
est
le
rayon
de
la
sphère
atomique
équivalente
au
volume
du
polyèdre
atomique
Vs
de
"Tigner
et
de
Seitz
(à).
En
comparant
le
volume
V,s
de
l’atome
subs-
titué
au
volume
qu’il
occuperait
dans
son
propre
métal
si
ses
atomes
étaient
comprimés
au
même
degré,
nous
avons
calculé
l’énergie
latente
de
la
solution
solide
et
nous
avons
supposé
que
cette
énergie
est
emmagasinée
dans
le
réseau
de
la
solution
solide
et
quelle
fait
baisser
son
point
de
fusion.
Article published online by EDP Sciences and available at http://dx.doi.org/10.1051/jphysrad:01937008010039100

392
Les
valeurs
de
l’énergie
latente
calculées
par
cette
méthode
ont
donné
des
écarts
considérables
par
rap-
port
aux:
données
expérimentales
déduites
des
dia-
grammes
thermiques
des
solutions
solides
étudiées.
Par
cette
méthode
de
calcul
on
ne
peut
pas
rendre
compte
du
changement
de
la
constante
de
réseau
de
la
solution
solide,
car
dans
le
cas
de
déformation
locale
de
Rosen-
hain
Co)
le
volume
atomique
moyen
de
la
solution
solide
reste
constant
et
la
constante
de
réseau
ne
change
pas.
Dans
ce
travail
nous
supposons
que
les
volumes
atomiques
du
métal
solvant
restent
constants
et
que
l’accroissement
de
volume
dû
à
la
substitution
de
l’atome
étranger
occupant
un
volume
atomique
Vs
se
traduit
par
unc
dilatation
de
volume
de
la
solution
solide
égale
à
Vs -
vo
par
atome
substitué.
Nous
aban-
donnons
l’hypothèse
d’une
perturbation
locale
dans
le
sens
de
Rosenhain
(~).
En
outre,
nous
introduisons
l’hypothèse
de
formation
des
couches
virtuelles
« s »
par
les
électrons
de
valence
de
l’atome
substitué,
c’est-
à-dire,
nous
les
traitons
comme
semi-libres
ou
semi-
liés
et
ceci
augmente
l’effet
écran.
Nous
n’étudions
que
les
solutions
solides
de Zn,
Ga,
Ge
dans
le
Cu
et
de
Cd,
In,
Sn,
Sb
dans
l’Ag.
Le
cas
de
la
solution
solide
Cu-Al
est
discuté,
nous
y
supposons
que
Al
en
solution
dans
le
Cu
possède
dans
une
certaine
mesure
des
propriétés
d’un
métal
de
transition.
2.
L’effet
écran
et
l’hypothèse
de
formation
des
couches
virtuelles
«
s ». -
En
substituant
un
atome
de
valence
-~-
1
dans
le
réseau
d’un
métal
monovalent,
son
potentiel
électrostatique +
(R)
à
une
distance R
de
son
centre
est
donné
par
l’équation
(1).
Pour
calculer 4)
(R),
Mott
(2)
applique
aux
électrons
de
valence
la
mâthode
de
Thomas
et
Fermi
en
les
traitant
comme
libres.
Mais
nous
savons
que
les
électrons
des
métaux
de
valence ~
+ 1
deviennent
de
plus
en
plus
liés
quand
croit,
les
atomes
métalliques
considérés
ont
une
tendance
croissante
à
entrer
en
liaisons
covalentes
et
à
se
lier
avec
leurs
voisins
suivant
la
règle
«
8
-
N »
de
Hume-Rothery
(6)
ou
suivant
la
règle
«
6
-
aV
o
de
Niven
(7),
qui
propose
de
changer
la
règle
de
Hume-
Rothery
en
ne
tenant
compte
que
des
électrons
p.
Nous
pouvons
donc
admettre
que
les
électrons
de
valence
de
ces
atomes
ne
sont
que
semi-libres,
leur
perte
partielle
de
«
liberté »
étant
causée
par
leur
tendance
à
former
des
couches
virtuelles
s
et p.
Nous
supposons
que
ces
couches
virtuelles
ne
pos-
sèdent
une
certaine
stabilité,
qu’à
partir
de z
-~-
1
=
3,
où
apparaît
le
premier
électron
~,
car
l’atome
substitué
en
remplaçant
dans
le
réseau
un
atome
du
métal
solvant
doit
fournir
en
première
approximation
aussi
au
moins
un
électron
libre,
et
la
formation
d’une
couche
virtuelle
« s
»
devient
possible.
Pour z
+ 1
>
3
des
couches
virtuelles
»
peuvent
se
constituer.
Dans
ce
qui
suit
nous
n’admettons
que
la
formation
d’une
couche
virtuelle
cc s
~>
et
nous
tenons
compte
de
la
formation
des
couches
virtuelles
«
p
»
en
posant
le
poids
de
la
tendance
de
formation
de
la
couche
virtuelle
cc
s
»
proportionnel
au
nombre £ p
des
électrons
p.
Cette
tendance
de
formation
des
couches
virtuelles
« s
»
dépendra
aussi
du
nombre
quantique
principal n
des
électrons
de
valence,
nous
supposons
qu’elle
est
inver-
sement
proportionnelle
à n
pour
les
solutions
solides
étudiées.
Nous
faisons
donc
l’hypothèse
que
le
poids
de
la
ten-
dance
de
formation
de
la
eouche
virtuelle
o s
»
est
pro-
portionnel
à
C. :
au
nombre
des
électrons
p
divisé
par
le
nombre
quantique
principal n
et
multiplié
par
une
constante
C,
dans
les
calculs
nous
posons
C
».1.
Ceci
n’est
qu’une
approximation,
pour
le
calcul
exact
au
lieu
de
la
conception
des
couches
virtuelles
« s
»
on
devait
évaluer,
en
se
servant
des
méthodes
de
la
méca-
nique
ondulatoire,
le
nombre
des
électrons
de
valence
dans
les
différentes
zones
énergétiques
dans
le
cristal,
zones
de
Brillouin
(8).
En
admettant
la
formule
de
Mott
et
l’hypothèse
de
formation
des
couches
virtuelles
« s »
nous
obtenons
la
valeur
de
l’énergie
latente
et
de
la
constante
de
réseau
des
solutions
solides
en
traitant
l’atome
substi-
tué
comme
un
centre
de
perturbation
d’une
charge
supplémentaire
positive
égale
à
au
lieu
de
ze
dans
l’équation
(1).
z’
est
donné
d’après
l’hypothèse
de
for-
mation
des
couches
virtuelles
« s
»
par
la
relation
Dans
la
formule
de
Mott
(1)
nous
remplaçons
donc
par z"
donné
par
(6),
et
l’équation
(1)
devient
et
tout
se
passe
comme
si z
avait
diminué
ou
comme
si
l’effet
écran
avait
augmenté..
3.
La
perturbation
du
réseau. -
Dans
l’article
précédent
(1)
nous
avons
admis
l’hypothèse
d’une
per-
turbation
locale
de
réseau
due
à
l’introduction
de
l’atome
substitué
et
nous
avons
obtenu
pour
la
densité
de
la
charge
électrique
positive
la
relation
(3).
Dans
ce
travail
nous
avons
remplacé
la
conception
de
pertur-
bation
locale
par
l’hypothèse
suivante :
«
La
loi
de
Mott
étant
admise
sous
la
forme
(7),
les
volumes
des
atomes
du
métal
solvant
entourant
l’atome
substitué
restent
constants,
mais
les
atomes
subissent
une
déformation
qui
change
leurs
volumes
atomiques
sphériques
(polyèdres
de
WigneretSeitz
(5»,
en volumes
atomiques
elliptiques,
c’est-à-dire
que
leur
degré
de
symétrie
dans
le
réseau
baisse.
»
Il
apparaît
donc
en
analogie
avec
(3)
une
densité
de
charge
positive
ou
une
perte
partielle
de
liberté
des
électrons
libres
des
atomes
du
métal
solvant
en
fonc-
tion
de
R,
distance
de
l’atome
substitué

393
L’apparition
de
p
(R)
en
direction
de
R
est
due
à
la
déformation V.
des
sphères
atomiques
qui
deviennent
des
ellipsoïdes,
dont
l’axe
de
rotation,
le
petit
axe,
est
parallèle
à
la
direction
(fig.
1
a,
b).
Nous
définis-
sons
la
déformation ~
par
le
rapport
des
volumes
de
deux
calottes,
obtenues
par
intersection
de
la
sphère
atomique
de
rayon
ro
avec
l’ellipsoïde,
au
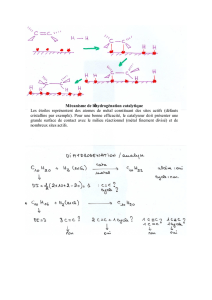
Fig.
1.
-
a)
Image
schématique
de
la
déformation
du
réseau
autour
de
l’atome
étranger
substitué,
dans
le
plan
(100).
b)
Image
schématique
de
la
déformation
de
la
sphère
atomique
en
ellipsoïde
de
rotation
de
même
volume
vo.
volume
de
la
sphère
atomique
vo
(fi-. 1
b).
Nous
obte
nons
ainsi
pour
p
d’après
les
relations
(4),
(6),
(8)
et
calculant
le
volume
0
vo
de
deux
calottes
(parties
poin-
tillées
sur
la
fig.
1
b)
en
tenant
compte
de
constance
de
volume,
équation
( i 9 ) :
Grâce
à
la
déformation V.
il
apparait
une
dissymétrie
du
degré
de
liberté
de
l’électron
libre
de
l’atome
déformé
qui
se
manifeste
par
une
perte
partielle
de
sa
liberté.
Nous
pouvons
donc
interpréter
la
relation
(8)
soit
par
apparition
de
surcharge
positive,
soit
par
une
liaison
partielle
de
l’électron
libre.
En
outre,
les
volumes
atomiques
vo
du
métal
solvant
étant
constants,
il
en
résulte
une
dilatation
(Vs >
vo)
ou
une
contraction
(Vs
vo)
de
la
solution
solide
étudiée.
4.
Calcul
des
de
l’énergie
latente
et
de
la
constante
de
réseau.
-
Les
métaux
Cu
et
Ag
cristal-
lisent
dans
le
système
cubique à
faces
centrées.
Un
cube
élémentaire
de
volume
_-_- ~
vo
contient
4
atomes
et
chaque
atome
possède
12
voisins.
Si
nous
rempla-
çons
un
des
atomes
du
métal
solvant
par
un
atome
étranger
de
valence z
-(-
1
et
voisin
dans
le
système
périodique
des
éléments,
son
volume
atomique
Vs
dans
le
réseau
du
métal
solvant
sera
différent
de
vo
et
la
constante
de
réseau
de
la
solution
solide
sera
diffé-
rente
de
la
constante
de
réseau
do
du
métal
solvant
pur.
Les
sphères
atomiques
de
rayon
ro
après
la
substi-
tution
de
l’atome
étranger
auron.
approximativement
t
la
forme
des
ellipsoïdes
de
rotation,
leur
rayon
équa-
torial
sera
égal
à
ro
(1
+
0)
et
leur
rayon
polaire
parallèle
à
R
sera
égal
à
ro
(1 -
2o)
(fig.
1
6),
car
nous
supposuns
que
le
volume
atomique
Vu
malgré
sa
défor-
mation y
reste
constant :
8
étant
égal
à V 2 3
u"
Pour
des
valeurs
faibles
de p
et
par
conséquent
aussi
de
o,
la
condition
(10)
est
remplie
parce
que
En
calculant
dans
la
relation
(9)
le
volume
de
deux
calottes
nous
y
avons
négligé
les
termes
d’ordre
supérieur
en ô
en
supposant
que
ô
est
petit.
Nous
pouvons
maintenant
calculer
le
volume
v,s
d’un
atome
étranger
substitué
dans
le
réseau
du
métal
solvent.
Traçons
autour
du
centre
0
d’un
des
atomes
du
métal
solvent
une
sphère
de
rayon
Ro
= ~
passant
par
les
centres
B
de
ses
douze
voisins
(fig
1.
a).
Subs-
tituons
à
l’atome
considéré
l’atome
étranger
de
valence
,~
+ 1.
Les
sphères
atomiques
de
ses
voisins
se
sont
alors
transformées
en
ellipsoïdes
déformés,
marqués
schématiquement
sur
la
figure
1
par
des
ellipsoïdes
réguliers
de
rotation,
dont
les
centres
sont
déplacés
en
A
(fig. 1
a).
Traçons
autour
de
0
une
sphère
de
rayon R =
OA.
Nous
pouvons
écrire
qu’approximativement
la
rela-
tion
suivante
existe
entre
R,
Ro,
ro
(
1
+
1)
et
)’0
(fig
1) :
Evaluons
le
volume
de
la
sphère
de
rayon R
en
intro-
duisant
les
volumes
atomiques
vo
et
Vs.
De
l’équation
(t~)
nous
obtenons
pour
Vs :

394
et
mettant
pour 1
sa
valeur
de
l’équation
(9) :
Dans
cette
équation,
nous
remplaçons
~o
par
ÔB
et
4
pour
R
nous
posons
sa
valeur
de
l’équation
(~3).
Pour
calculer
Vs
à
l’aide
de
l’équation
(21)
nous
posons
en
première
approximation
dans
l’expression
due, 4
donnée
par
(20)
une
valeur
probable
pour
Vs!vo
et
après
le
premier
calcul
nous
obtenons
facilement
la
valeur
finale
de
V~.
Connaissant
V,~
nous
calculons
l’énergie
latente
~s
de
la
solution
solide,
Vs
>
1)0
en
la
comparant
au
travail
de
dilatation
-
équivalent,
pour
des
faibles
concentrations
du
métal
en
solution,
au
travail
de
compression
du
métal
solvant :
où X
est
le
coefficient
de
compressibilité
du
métal
solvant.
Pour
obtenir
la
constante
de
réseau
dx
de
la
solution
solide
pour
une
concentration
de x
atomes
pour
i 00
subs-
titués,
nous
calculons
le
volume
atomique
moyen
correspondant
à
la
concentration
x.
Nous
avons
la
relation
et
nous
obtenons
pour
dx :
Pour
calculer
rabaissement
du
point
de
fusion
~1 T
de
la
solution
solide,
nous
posons
6s
=
3 ~ I’.
La
tem-
pérature
T
déduite
de
cette
relation
est
à
multiplier
par la
concentration
correspondante
x
des
atomes
en
solution
pour
obtenir
à
T.
Dans
le
tableau
1 les
gran-
l’
et
sont
calculées
pour (1:
# 1
100,
Les
résultats
obtenus
sont
donnés
dans
le
tableau
1
où
figurent ;
1.
La
solution
solide
étudiée,
le
métal
indiqué
le
premier,
Cu
ou
Ag,
est
le
solvant ;
2.
z",
d’après
l’équation
(6) :
3.
d’après
l’équation
(21) ;
4.
’0s
en
e V,
d’après
l’équation
(i$2) j
5. A
Tcal,
l’abaissement
du
point
de
fusion
de
la
solution
solide
calculé
pour
une
concentration
x
=
1
pour
100 ;
6.
0
T,,tii.,
l’abaissement
du
point
de
fusion
de
la
solution
solide
de
même
concentration
x û
1
pour
100
d’après
les
valeurs
expérimentales
dans
les
diagrammes
thermiques
-
phase
(1.,
courbe
du
solidus
-
repro-
duits
dans
le
livre
de
Hume-Rothery
(6) ;
7.
(d/do),,al,..,d"après
l’équation
(24)pour x===l
pour 100 ;
8.
déduit
des
valeurs
expérimentales
pour
une
concentration
~===1
pour
100;
nous
y
avons
mis
deux
valeurs,
la
première
est
déduite
pour
le
minimum,
la
deuxième
pour
le
maximum
de
concentration
du
métal
en
solution
d’après
les
résultats
expérimentaux
de
Hume-Ruthery,
Lewin
et
Reynolds
(9).
Pour
la
solution
solide
Cu-Al,
les
données
expérimentales
de
sont
déduites
des
résultats
expérimentaux
de
0 ven et
Preston
(10).
Dans
les
calculs
de
iZs
et
nous
avons
employé
les
valeurs
de
la
constante
de
réseau
données
par
Hume-Rothery,
Lewin
et
Reynolds
(9).
avec
ces
valeurs
de
do,
nous
avons
calculé
r~
d’après
l’équation
(2)
et
nous
avons
obtenu
q = 4 ,807
.~-1
pour
le
Cu
et
1,700
Â-1
pour
Ag.
Les
valeurs
de y
dans
la
formule
(2)
pour
le
calcul
de
’iSs
sont
prises
des
tables
(1~).
Dans
le
cas
de
la
solution
solide
Cu-Al
apparaît
une
grande
différence
entre ;
T
calculé
et
à
T
solid.
Pour
expliquer
cet
écart,
nous
remarquons
que
les
électrons
de
valence
de
Al
substitué
dans
le
Cu
ont
plusieurs
états-
zones
énergétiques, 3 s,
3
p,
3 d, 4
s, , .
La
tendance
de
former
une
couche
cc s »
se
répartirait
donc
sur
plusieurs
états
énergétiques,
il
y
aurait
alors
aussi
une
certaine
tendance
d’occuper
la
zone
3 d et
l’Al
introduit
dans
le
réseau
de
Cu
aurait
dans
une
certaine
mesure
les
pro-
priétés
d’un
métal
de
transition
du
groupe
Fe,
Co,
Ni.
Le
diagramme
thermique
de
Cu-Ni
nous
montre
que
la
substitution
de 1
atome
pour
100
de
Ni
dans
le
réseau
de
Cu
élève
le
point
de
fusion
de
la
solution
solide
Cu-Ni
de
4°
environ
(’2).
D’après
les
données
de
Oven
et
Preston
~’°)~
la
constante
de
réseau
de
la
solution
solide
Cu-Ni
diminue
et
pour
1
atome
de
Ni
pour
100
elle
est
égale 4
0,99970
do.
Si
nous
supposons
que
Al
possède
dans
le
CU
des
propriétés
d’un
méta]
de
transi-
 6
6
 7
7
1
/
7
100%