Mouvement des charges dans un conducteur, conduction du courant

Mouvement des charges dans un conducteur,
conduction du courant
!"#$%&%'()(*%+&,-#%).%/)01%2(+"'/)1,3+%/).4'/)#')2"'.#2(%#+)5)
64)&"7%''%).%)2%8%)$,(%//%)%/()vectoriellement)'#11%)24+)1%/)2"11,/,"'/)9,'(%+42:"'/;)
4$%2)14)/(+#2(#+%)2+,/(411,'%).#)&0(41)+0<4+://%'()4104(",+%&%'()14).,+%2:"').#)
$%2(%#+)$,(%//%).%)2*4-#%)<4+:2#1%=)
>?)6%)&"#$%&%'()(*%+&,-#%)'%)(+4'/<"+(%)<4/).%)2*4+@%)%')&"7%''%=)A1)'%)<+".#,()
<4/).%)!"#$%&'=)
B%<%'.4'()1C4<<1,24:"').C#')2*4&<)01%2(+,-#%)
.4'/)#')2"'.#2(%#+)$4)@0'0+%+)#')&"#$%&%'()
&"7%').%/)01%2(+"'/)1,3+%/).4'/)2%1#,D2,)9-#,)'C%/()
."'2)<1#/)()*+,-#.*./$0;)
+
Sous+l’ac1on+du+champ+E,+le+gaz+d’électron+
acquiert+une+vitesse+moyenne+ve+non<nulle++

Courant et densité volumique de courant
E')'"(%)F%)14).%'/,(0)$"1#&,-#%).%)2*4+@%).%/),*0!'$"&1)20)!"&2#!3"&=)G"#+)1%)2#,$+%H)
-#,)%/()#')(+I/)3"')2"'.#2(%#+H)"')4)(7<,-#%&%'())
J"+/)0-#,1,3+%)9%')<+0/%'2%).%)2*4&<)01%2(+,-#%;H)2%/)01%2(+"'/)/"'()4',&0/).C#'%)
$,(%//%).C%'/%&31%)$%=)E').0K',()la+densité+volumique+.%)2"#+4'()2"&&%)5)
6%)2"#+4'()A)L)(+4$%+/)#'%)/#+M42%)N)9<4+)%O%&<1%)14)/%2:"').C#')K1)2"'.#2(%#+;)%/()
.0K',)2"&&%)14)-#4':(0).%)2*4+@%)(+4$%+/4'()2%8%)/#+M42%)<4+)#',(0).%)(%&</)5))
d2q=ene~vedt ·~ dS
9P=&DQ;)
9P;)

Conservation de la charge,
conservation du courant
6%)3,14').%)2*4+@%).4'/)#')$"1#&%)R).01,&,(0)<4+)#'%)/#+M42%)M%+&0%)N)/C02+,()
E#)%'2"+%H)/"#/)M"+&%)1"241%)9%')4<<1,-#4'()1%)(*0"+I&%).%)S+%%'DE/("@+4./T7;)H)
En+régime+sta1onnaire+9.U.()>)V;H)2%8%)<+"<+,0(0)/%)(+4.#,()<4+)14)2"'/%+$4:"').#)
2"#+4'()1%)1"'@).C#')'#/0)20)!"#$%&')9@0'0+41%&%'()1%)(#3%)>)#')K1)01%2(+,-#%4)5)
d⌧

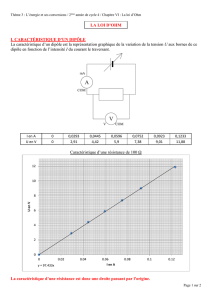
La loi d’Ohm
A1)%O,/(%)#'%)+%14:"')9$41431%).4'/)1C4<<+"O,&4:"').%)2*4&<)W)6%1)'$"6)7$%&21;)
%'(+%)1%)2*4&<)4<<1,-#0)%()14).%'/,(0)$"1#&,-#%).%)2"#+4'(),'.#,(%)<4+)2%)2*4&<))
γ+est+appelée+conduc1vité+du+milieu=)BC%/()#'%)@+4'.%#+)-#,)'%).0<%'.)-#%).%)14)
'4(#+%).#)2"'.#2(%#+=)W11%)/%)&%/#+%)%')N,%&%'/)<4+)&I(+%)5)NU&))
E').0K',()14)résis1vité+du+milieu+9'"(0%)%')@0'0+41)F;)comme+l’inverse+de+γ=)N"')
#',(0)%/()1CE*&)D)&I(+%)5)X=&)
6,%')%'(+%)+0/,/:$,(0)%()Y)$,/2"/,(0)Z)9&".I1%).%)[+#.%H)\]VV;)5)
dve
dt
=
eE
me
⌫eve
^02%//4,+%)<"#+)
Y)+%<+".#,+%)Z)9%')+%@=)
<%+&4'%'(;))14)<+"<"+:"''41,(0)
"3/%+$0%)%'(+%)$%)%()W)
E')"3:%'()5))
=
nee2
me⌫e
9M"'2:"').%)'%)&4,/)4#//,).%)_)L)(+4$%+/)`%;)

Retour à l’équilibre d’un « conducteur » en l’absence
de champ extérieur imposé
W')2"&3,'4'()14)2"'/%+$4:"').%)14)2*4+@%H)14)1",).CE*&)%()1C0-#4:"').%)!4Oa%11DS4#//H))
6C"+.+%).%)@+4.%#+).%)14)2"'.#2:$,(0).4'/).,b0+%'(/)&,1,%#O)5)
P,'/,H)1%)(%&</).%)+%("#+)L)1C0-#,1,3+%).C#')&4(0+,4#)/#+)1%-#%1)"')4).0<"/0).%)14)2*4+@%)
<%#()$4+,%+)%'(+%)\VD\c/)<"#+)1%)2#,$+%H)L)\V]/)9Qd)4'/e;)<"#+)1%)<"17/(7+I'%=)B%)(%&</)%/()
.C%'$,+"')\/)<"#+)1%)$%++%=)
4$%2)
On+peut+ainsi+définir+plus+quan1ta1vement+la+no1on+d’isolant+ou+de+conducteurH)%')
M"'2:"').%/)02*%11%/).%)(%&</)2"'/,.0+0%/).4'/)#')<+"31I&%)."''0=)