Loi Binomiale Activité introduction: la planche de Galton

Chapitre XII Loi Binomiale
Activité introduction: la planche de Galton
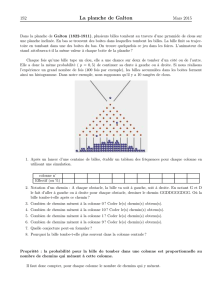
Dans la planche de Galton, plusieurs billes tombent au travers d'une pyramide de clous
sur une planche inclinée. En bas se trouvent des boîtes dans lesquelles tombent les billes.
La bille finit sa trajectoire en tombant dans une des boîtes du bas. On trouve quelquefois
ce jeu dans les foires. L'animateur du stand attribuera-t-il la même valeur à chaque boîte
de la planche ?
Chaque fois qu'une bille tape un clou, elle a une chance sur deux de tomber d'un côté ou
de l'autre. Elle a donc la même probabilité ( 0,5p) de continuer sa chute à gauche ou à
droite. Si nous réalisons l'expérience un grand nombre de fois (400 fois par exemple), les
billes accumulées dans les boîtes forment ainsi un histogramme.
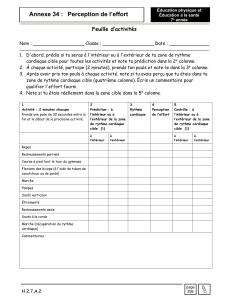
1) Après un lancer d'une centaine de billes, établir un tableau des fréquences pour
chaque colonne (à l’aide de la calculatrice – programme GALTON).
Cas où il y a 10 rangées de clous.
Colonne nº 0
1 2 3 4 5 6 7 8 9 10
effectif
(ou %)
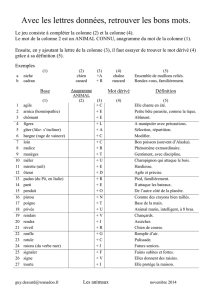
2) Notation d'un chemin : A chaque obstacle, la bille va soit à gauche, soit à droite.
En notant G et D le fait d'aller à gauche ou à droite pour chaque obstacle, dessiner
le chemin GGDDGGGDGG. Où la bille tombe-t-elle après ce chemin?
a) Combien de chemins mènent à la colonne 0 ? Coder le(s) chemin(s) obtenu(s).
b) Combien de chemins mènent à la colonne 10 ? Coder le(s) chemin(s) obtenu(s).
c) Combien de chemins mènent à la colonne 1 ? Coder le(s) chemin(s) obtenu(s).
d) Combien de chemins mènent à la colonne 9 ? Coder le(s) chemin(s) obtenu(s).
e) Quelle conjecture peut-on formuler ?
f) Pourquoi la bille tombe-t-elle plus souvent dans la colonne centrale ?

Propriété: la probabilité pour la bille de tomber dans une colonne est proportionnelle au
nombre de chemins qui mènent à cette colonne.
3) Il faut donc compter, pour chaque colonne le nombre de chemins qui y mènent.
Soit X la variable aléatoire qui compte le nombre d’apparition de la lettre D dans chaque
chemin.
Donner la loi de probabilité de X à partir de l’arbre ci-dessus.
k
P X k
En déduire l’espérance de cette variable aléatoire

On obtient le triangle de Pascal, connu des chinois dès le 14eme siècle