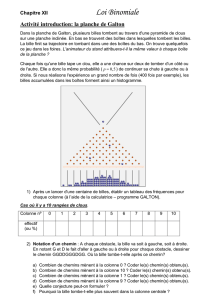
La planche de Galton

1S2 La planche de Galton Mars 2015
Dans la planche de Galton (1822-1911), plusieurs billes tombent au travers d’une pyramide de clous sur
une planche inclinée. En bas se trouvent des boîtes dans lesquelles tombent les billes. La bille finit sa trajec-
toire en tombant dans une des boîtes du bas. On trouve quelquefois ce jeu dans les foires. L’animateur du
stand attribuera-t-il la même valeur à chaque boîte de la planche ?
Chaque fois qu’une bille tape un clou, elle a une chance sur deux de tomber d’un côté ou de l’autre.
Elle a donc la même probabilité ( p= 0,5) de continuer sa chute à gauche ou à droite. Si nous réalisons
l’expérience un grand nombre de fois (400 fois par exemple), les billes accumulées dans les boîtes forment
ainsi un histogramme. Dans notre exemple, nous supposons qu’il y a 10 rangées de clous.
1. Après un lancer d’une centaine de billes, établir un tableau des fréquences pour chaque colonne en
utilisant une simulation.
colonne n˚
Effectif (ou %)
2. Notation d’un chemin : A chaque obstacle, la bille va soit à gauche, soit à droite. En notant G et D
le fait d’aller à gauche ou à droite pour chaque obstacle, dessiner le chemin GGDDGGGDGG. Où la
bille tombe-t-elle après ce chemin ?
3. Combien de chemins mènent à la colonne 0 ? Coder le(s) chemin(s) obtenu(s).
4. Combien de chemins mènent à la colonne 10 ? Coder le(s) chemin(s) obtenu(s).
5. Combien de chemins mènent à la colonne 1 ? Coder le(s) chemin(s) obtenu(s).
6. Combien de chemins mènent à la colonne 9 ? Coder le(s) chemin(s) obtenu(s).
7. Quelle conjecture peut-on formuler ?
8. Pourquoi la bille tombe-t-elle plus souvent dans la colonne centrale ?
Propriété : la probabilité pour la bille de tomber dans une colonne est proportionnelle au
nombre de chemins qui mènent à cette colonne.
Il faut donc compter, pour chaque colonne le nombre de chemins qui y mènent.

1S2 La planche de Galton Mars 2015
Soit Xla variable aléatoire qui compte le nombre d’apparitions de la lettre D dans chaque chemin.
Donner la loi de probabilité de Xà partir de l’arbre ci-dessus.
k=
P(X=k)
En déduire l’espérance de cette variable aléatoire.
On a retrouvé ce document en Chine au 14ème siècle.
Le décrypter.