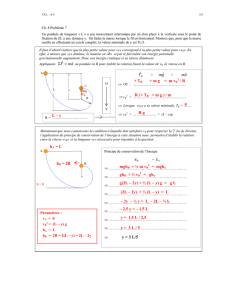
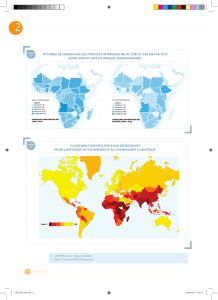
Présentation générale de la cinématique du solide ( CIR

MOUVEMENT PLAN
ÉQUIPROJECTIVITÉ
Soient deux points A et B appartenant à un même solide S,
Les projections orthogonales sur AB des vecteurs vitesses
VA€S/R VB€S/R sont égales :
AH = BK
A
B
VA€S/R
VB€S/R
H
K
Pour pouvoir appliquer cette propriété, il faut connaître :
intégralement une des 2 vitesses
le support de la seconde

MOUVEMENT PLAN
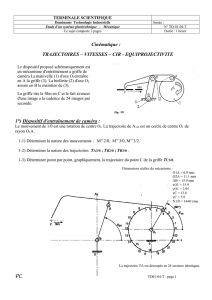
EXEMPLE :système vilebrequin(1)-bielle(2)-piston(3)
Connaissant la vitesse en rotation du vilebrequin, déterminer graphiquement la vitesse linéaire du piston.
1/0 = 100 rad.s-1
OA=30mm
VA1/0 = ω.R = 100 ×0.03 = 3 m/s
VA1/0
La bielle 2 et le piston 3 sont articulés au pt B donc :
VB3/0 VB2/0
=
Le piston 3 est en Mvt de translation rectiligne, donc la trajectoire du pt B est la droite OB
La droite OB est le support de VB3/0 VB2/0
et
HK
VB2/0
mesurer Bb : mm VB3/0 = m.s-1
25 2.5

MOUVEMENT PLAN
DOUBLE EQUIPROJECTIVITÉ
Si l’on connaît intégralement les vitesses de 2 points d’un solide,
on peut déterminer la vitesse de tout autre point en appliquant 2 fois l’équiprojectivité
A
B
C
VA
VC
VB
A1C1
B2
C2
La méthode est impossible de cette façon si les 3 points sont alignés.
Il faut alors utiliser la méthode du CIR

MOUVEMENT PLAN
Centre instantané de rotation : CIR
Dans tout solide en mouvement plan, il existe un seul point ayant une vitesse nulle à un instant donné.
On l’appelle Centre Instantané de Rotation.
AB
C
VA
VB
VC VA
B
CA
O
O
Le pt O est le CIR
La vitesse est proportionnelle au rayon
OA >OC >OB donc :
VC VBVA >>
VC
VB

MOUVEMENT PLAN
B
A
EXEMPLE 1:
A
V
V A= 4 m/s
CIR
B
V
Vc
V B= 3,6 m/s
V C= 5,1 m/s
C