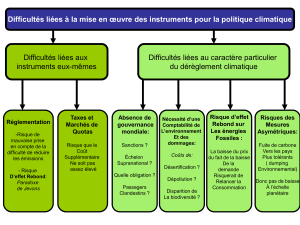
Thème : ESPACE ET MOUVEMENT
1
Thème : ESPACE ET
MOUVEMENT
Rebond d’une balle
2
Etude du rebond d’une balle (1) .
Expérimentation :
•Une caméra web
permet de filmer le
mouvement d’une
balle lâchée sans
vitesse initiale.
3
Etude du rebond d’une balle (2).
Expérimentation :
•Sur cette vidéo numérique
le logiciel AVIMECA
permet d’effectuer des
mesures de position du
centre de la balle, image
par image, donc à des
dates successives connues.
4
On obtient ainsi:
•Les abscisses yidu
centre sur un axe
vertical dirigé vers le
bas .
•Les dates de passage
tià ces abscisses .
5
Utilisation d’un tableur
Ce tableau de
mesures peut être
exporté vers un
tableur pour calculer
les vitesses v
instantanées et pour
représenter
graphiquement y et v
au cours du temps t
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
1
/
51
100%
