CSI2510 Structures de données et algorithmes Automne 2009

1
CSI2510
Structures de données et
algorithmes
Arbres couvrants minimaux
1

Arbre couvrant minimal (Minimum spanning
tree)
Définitions
L'algorithme de Prim-Jarnik
L'algorithme de Kruskal
2
CSI2510 - ACM

Arbre couvrant minimal
Sous-graphe couvrant
Sous-graphe d’un graphe G
contenant tous les sommets de
G
Arbre couvrant
Sous-graphe couvrant qui est un
arbre
Arbre couvrant minimal (ACM)
Arbre couvrant d’un graphe
pondéré avec la somme
minimale de poids des arêtes
constituant l'arbre
Applications
Réseaux informatiques
Réseaux routiers
ORD
PIT
ATL
STL
DEN
DFW
DCA
10
1
9
8
6
3
2
5
7
4
3
CSI2510 - ACM

ACM versus PCC
CSI2510 - ACM 4 4
ORD
PIT
ATL
STL
DEN
DFW
9
1
9
8
6
3
2
5
7
4
DCA
ORD
PIT
ATL
STL
DEN
DFW
9
1
9
8
6
3
2
5
7
4
DCA
Arbre couvrant minimal Arbre des plus courts chemin

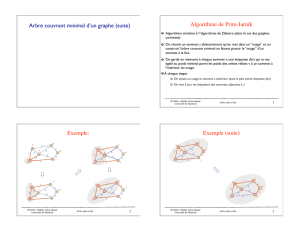
Propriété des cycles
Soit Tun arbre couvrant minimal
d’un graphe pondéré G
Soit eune arête de G
n’appartenant pas à T et soit Cle
cycle obtenu lorsqu’on ajoute eà
T
Pour chaque arête fdans C,
poids(f)poids(e)
Preuve:
Par contradiction
Si poids(f)> poids(e) nous
pouvons obtenir un arbre
couvrant de plus petit poids en
remplaçant epar f
8
4
23
6
7
7
9
8
e
C
f
8
4
23
6
7
7
9
8
C
e
f
Remplacer favec e produit un
meilleur arbre couvrant
5
CSI2510 - ACM