CSI2510 Structures de données et algorithmes Arbres couvrants

1
1
CSI2510
Structures de données et
algorithmes
Arbres couvrants minimaux
1
Arbre couvrant minimal (Minimum spanning
tree)
Définitions
L'algorithme de Prim-Jarnik
L'algorithme de Kruskal
2
CSI2510 - ACM
Arbre couvrant minimal
Sous-graphe couvrant
Sous-graphe d’un graphe G
contenant tous les sommets de
G
Arbre couvrant
Sous-graphe couvrant qui est un
arbre
Arbre couvrant minimal (ACM)
Arbre couvrant d’un graphe
pondéré avec la somme
minimale de poids des arêtes
constituant l'arbre
Applications
Réseaux informatiques
Réseaux routiers
ORD
PIT
ATL
STL
DEN
DFW
DCA
10
1
9
8
6
3
2
5
7
4
3
CSI2510 - ACM
ACM versus PCC
CSI2510 - ACM 4 4
ORD
PIT
ATL
STL
DEN
DFW
10
1
9
8
6
3
2
5
7
4
DCA
ORD
PIT
ATL
STL
DEN
DFW
10
1
9
8
6
3
2
5
7
4
DCA
Arbre couvrant minimal Arbre des plus courts chemin

2
Propriété des cycles
Soit Tun arbre couvrant minimal
d’un graphe pondéré G
Soit eune arête de G
n’appartenant pas à T et soit Cle
cycle obtenu lorsqu’on ajoute eà
T
Pour chaque arête fdans C,
poids(f)≤
≤≤
≤poids(e)
Preuve:
Par contradiction
Si poids(f)>
> >
> poids(e) nous
pouvons obtenir un arbre
couvrant de plus petit poids en
remplaçant epar f
8
4
23
6
7
7
9
8
e
C
f
8
4
23
6
7
7
9
8
C
e
f
Remplacer favec e produit un
meilleur arbre couvrant
5
CSI2510 - ACM
Dans tout cycle du graphe,
les arêtes faisant partie d’un
ACM ont des poids
inferieurs aux autres arêtes
(en pointillé)
ORD
PIT
ATL
STL
DEN
DFW
DCA
10
1
9
8
6
3
2
5
7
4
6
CSI2510 - ACM
Propriété des cycles
U V
Propriété de partition
Propriété de partition:
Considérons une partition des
sommets de G en deux ensembles U
et V. Soit e une arête de poids
minimal entre U et V. Alors, il existe
un arbre couvrant minimal de G
contenant e
Preuve:
Soit Tun arbre couvrant minimal de G
Si Tne contient pas e, soit Cle cycle
formé par l’addition de eà T et soit fune
arête de Centre U et V
Par la propriété de cycles,
poids(f)≤
≤≤
≤poids(e)
Alors, poids(f)=
= =
= poids(e)
Nous obtenons un autre ACM en
remplaçant f par e
7
4
28
5
7
3
9
8e
f
7
4
28
5
7
3
9
8e
f
Remplacer favec e
donne un autre ACM
U V
7
CSI2510 - ACM
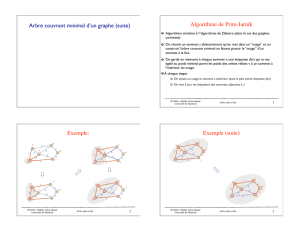
L’algorithme de Prim-Jarnik
L'algorithme de Prim-Jarnik pour calculer un ACM est
similaire à l'algorithme de Dijkstra
Nous supposons que le graphe est connexe
Nous choisissons un sommet arbitraire set nous faisons
grossir l’ACM comme un nuage de sommets, commençant
de s
Nous emmagasinons avec chaque sommet vune étiquette
d(v)représentant le plus petit poids d'une arête reliant và un
sommet du nuage (au lieu de la somme totale des poids sur
un chemin du sommet de départ jusqu’à vdans Dijkstra)
8
CSI2510 - ACM

3
L’algorithme de Prim-Jarnik
Pour chaque étape
Nous ajoutons au nuage le sommet extérieur uayant la
plus petite étiquette de distance
Nous mettons à jour les étiquettes des sommets adjacents
à u
9
CSI2510 - ACM
Utiliser une file à priorité Qdont les clés sont les étiquettes D, et dont
les éléments sont des paires sommet-arête
Clé : distance
Élément: (sommet, arête de poids minimal)
Tout sommet vpeut être le sommet de départ (D[v] =0)
On initialise toutes les valeurs de D[u] à “infini”, mais nous
initialisons aussi E[v] (l’arête associé à v) à “null”
Retourne l’arbre recouvrant minimal T.
Nous pouvons réutiliser le code produit par Dijkstra, et ne changer que quelques parties. Observons
le pseudo-code....
10CSI2510 - ACM
L’algorithme de Prim-Jarnik
Algorithm PrimJarnik(G):
Entrée: Un graphe pondéré G.
Sortie: Un ACM Tpour G.
Choisir un sommer v de G
{bâtir l’arbre à partir de v}
T ←{∅}
D[v] ←0
E[v] ←null
Pour chaque sommet u ≠ v faire
D[u] ←∞
Soit Q une file à priorité contenant des sommets avec les étiquettes D comme clé
Tant que Q n’est pas vide
(u,E(u)) ←Q.removeMinElement()
ajouter le sommet u et l’arête E[u] à T
Pour chaque sommet z adjacent à u et dans Q
{effectuer la relaxation de l’arête (u, z) }
if poids(u, z) < D[z] then
D[z] ←weight(u, z)
E[z] ←(u, z)
mettre à jour D[z]
retourner l’arbre T 11CSI2510 - ACM
Prim-Jarnik: Exemple
B
D
C
A
F
E
7
4
28
5
7
3
9
8
07
2
8∞
∞∞
∞
∞
∞∞
∞
B
D
C
A
F
E
7
4
28
5
7
3
9
8
07
2
5∞
∞∞
∞
7
B
D
C
A
F
E
7
4
28
5
7
3
9
8
07
2
5∞
∞∞
∞
7
B
D
C
A
F
E
7
4
28
5
7
3
9
8
07
2
54
7
12
CSI2510 - ACM

4
B
D
C
A
F
E
7
4
2
8
5
7
3
9
8
03
2
54
7
B
D
C
A
F
E
7
4
2
8
5
7
3
9
8
03
2
54
7
13
CSI2510 - ACM
Prim-Jarnik: Exemple ACM versus PCC
CSI2510 - ACM 14
CB
A
E
D
F
0
4
28
∞
∞∞
∞ ∞
4
8
7 1
25
2
3 9
CB
A
E
D
F
0
1
27
39
4
8
71
25
2
3 9
CB
A
E
D
F
0
4
8
71
2 5
2
3 9
2
8
∞
∞∞
∞ ∞
∞∞
∞
4
3
11
5
PRIM
(Minimum Spanning Tree)
Djkstra
(Shortest Path Spanning Tree)
48
∞
∞∞
∞ ∞
L’algorithme applique la propriété des cycles
Soit (u,v) l’arête minimale pour une itération donnée.
S’il y a un ACM ne contenant pas (u,v), alors (u,v)
complète un cycle. Puisque (u,v) a été préférée à toute
autres arête connectant v au groupe, elle doit avoir un
poids inférieur ou égal au poids de l’autre arête. Un
nouveau ACM peut être formé par permutation
15
CSI2510 - ACM
Prim-Jarnik Prim-Jarnik: Analyse de complexité
Opérations sur les graphes:
Méthode incidentEdges est appelée une fois pour chaque
sommet
Opérations d’étiquetage:
Nous plaçons/obtenons les étiquettes du sommet z O (deg( z ))
fois
placer/obtenir les étiquettes prend O (1)
Opérations de file de priorité (implémenté par un tas):
Chaque sommet est inséré une fois et enlevé une fois de la file à
priorité, où chaque insertion ou suppression prend O (log n )
La clé d'un sommet w dans la file à priorité est modifiée au plus
deg( w ) fois, où chaque changement de clé prend O (log n )
16
CSI2510 - ACM

5
L’algorithme de Prim-Jarnik est exécuté en O (( n + m ) log n )
si le graphe est représenté par la structure de liste d’adjacence (et en
utilisant un tas)
Rappelez-vous que S
v
deg( v ) = 2 m
Le temps d’exécution est O ( m log n ) parce que le graphe est
connexe
17
CSI2510 - ACM
Prim-Jarnik: Analyse de complexité Dijkstra vs. Prim-Jarnik
Algorithm PrimJarnikMST(G)
Q ←new heap-based priority queue
s ←a vertex of G
for all v ∈G.vertices()
if v= s
setDistance(v, 0)
else
setDistance(v, ∞
∞∞
∞)
setParent(v, ∅
∅∅
∅)
l ←Q.insert(getDistance(v), v)
setLocator(v,l)
while !Q.isEmpty()
u ←Q.removeMin()
for all e ∈G.incidentEdges(u)
z ←G.opposite(u,e)
r ←weight(e)
if r< getDistance(z)
setDistance(z,r)
setParent(z,e)
Q.replaceKey(getLocator(z),r)
Algorithm DijkstraShortestPaths(G, s)
Q ←new heap-based priority queue
for all v ∈G.vertices()
if v= s
setDistance(v, 0)
else
setDistance(v, ∞
∞∞
∞)
setParent(v, ∅
∅∅
∅)
l ←Q.insert(getDistance(v), v)
setLocator(v,l)
while !Q.isEmpty()
u ←Q.removeMin()
for all e ∈G.incidentEdges(u)
z ←G.opposite(u,e)
r ←getDistance(u) + weight(e)
if r< getDistance(z)
setDistance(z,r)
setParent(z,e)
Q.replaceKey(getLocator(z),r)
18
CSI2510 - ACM
L’algorithme de Kruskal
Chaque sommet est emmagasiné initialement comme son propre
groupe.
A chaque itération, l’arête de poids minimal dans le graphe est
ajoutée à l'arbre couvrant si elle relie 2 groupes distincts.
L'algorithme se termine quand tous les sommets sont dans le
même groupe.
19
CSI2510 - ACM
Ceci est une application de la propriété de partition!
Si l’arête minimale pour une itération donnée est (u,v), alors
si nous considérons une partition de G avec udans un
groupe et vdans l’autre, alors la propriété de partition dit
qu’il doit y avoir un ACM contenant (u,v)
Une file à priorité
emmagasine les arêtes
extérieures (hors du nuage)
clé: poids
élément: arête
À la fin de l’algorithme
On se retrouve avec un
nuage qui entoure
l’ACM
Un arbre T qui est notre
ACM
Algorithm KruskalMST(G)
Pour chaque sommet Vdans Gfaire
définir Cloud(v) de {v}
Soit Qune file à priorité.
Insérer toutes les arête dans Qen
utilisant leur poids comme clé
T∅
∅∅
∅
Tant que Ta moins que n-1 sommets
Faire
sommet e= Q.removeMin()
Soit u, vles extrémités de e
Si Cloud(v) ≠
≠≠
≠Cloud(u) alors
ajouter arête eà T
Fusionner Cloud(v) et Cloud(u)
return T
20
CSI2510 - ACM
L’algorithme de Kruskal