Une dioptre CONCAVE fait DIVERGER les rayons → R < 0 Une

Dernier cours …
•Dioptre est une surface sphérique.
•Une lentille possède deux dioptres.
•Convention des signes:
•Une dioptre CONCAVE fait DIVERGER les rayons → R < 0
•Une dioptre CONVEXE fait CONVERGER les rayons → R > 0
•La lentille est une combinaison de deux dioptres.
•Si l’assemblage fait CONVERGER les rayons, elle est dite
CONVERGENTE et sa distance focale f > 0
•FOYER OBJET situé du côté OBJET
•FOYER IMAGE situé du côté IMAGE RÉELLE
•Si l’assemblage fait DIVERGER les rayons, elle est dite
DIVERGENTE et sa distance focale f < 0
•FOYER OBJET situé du côté OPPOSÉ à l’objet
•FOYER IMAGE situé du côté OBJET
•IMAGE RÉELLE est situé du côté de la lentille OPPOSÉ à
l’OBJET → q > 0 et p > 0
•IMAGE VIRTUELLE est situé du même côté de la lentille que
l’OBJET → q < 0 et p > 0

Dioptres
Convexe, Convergente, R > 0, p > 0, q > 0, m < 0
Concave, Divergente, R < 0, p > 0, q < 0, m > 0

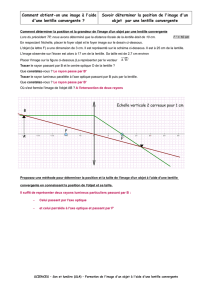
Rayons principaux (approximation paraxiale)
1. Rayon passant par le centre de la lentille
n’est pas dévié
2. Rayon parallèle à l’axe optique ressort en
passant par le foyer image F’
3. Rayon passant par le foyer Fressort
parallèle à l’axe optique
Objet Image Objet
Image
Lentille divergente
f < 0, p > 0, q < 0, m > 0 Lentille convergente f > 0, p > 0, q > 0, m < 0

Équations importantes
•Formule des dioptres sphériques
•Grandissement transversal des dioptres sphériques
•Formule des opticiens
•Formule des lentilles minces
•Convention des signes:
•lentille convergente → f > 0
•lentille divergente → f < 0
•Grandissement transversal pour une lentille mince
•Grossissement
211
12 111 RRn nn
f
Rnn q
n
p
n1221 
p
q
n
n
y
y
mO
I
2
1
qpf 111 
p
q
y
y
mO
I
G

Loupe
•Lentille convergente qui donne un
image virtuelle agrandie