Agrandissement d`un petit objet. Position du problème On a une

Agrandissement d’un petit objet.
Position du problème
On a une lentille convergente de vergence V= 50 δ. Sa distance focale image est :
f′=1
V
A.N. : f′=1
50 = 2,0 cm
On a un petit objet AB tel que :
A(L) −−→ A′
B(L) −−→ B′
avec AB = 5,0·10−1cm
On recherche la position de l’objet par rapport à la lentille (i.e. OA) permettant d’obtenir un grandissement γ=
A′B′
AB = 5,0.
1 . D’après la relation de conjugaison de Descartes, on a :
1
OA′
−1
OA =1 OF ′(1)
Or le grandissement de la lentille vérifie :
γ=OA′
OA
⇐⇒ OA′=γ OA (2)
En injectant (2) dans (1), il vient :
1
γ−11
OA =1
f′⇐⇒ OA =f′1−γ γ
A.N. : OA = 2,01−5,0
5,0=−1,6 cm
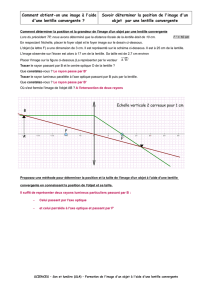
2 . Les différentes étapes de la construction permettant de vérifier le résultat précédent sont détaillées ci-dessous :
• On trace l’axe optique.
• On place l’objet AB tel que AB = 5,0·10−1cm.
• On place le foyer principal objet Fsachant que
γ=F O
F A
⇐⇒ F A =f′
γ
A.N. : F A =2,0
5,0= 4,0·10−1cm
• On place la lentille convergente sachant que F O =f′= 2,0 cm.
• On trace le rayon incident issu de Bpassant par O. Il n’est pas dévié lors de la traversée de la lentille.
• On trace le rayon incident issu de Bdont le prolongement passe par F. Il émerge de la lentille parallèlement à
l’axe optique
• L’image B′se trouve dans le prolongement des rayons qui émergent de la lentille.
• L’image A′se trouve à l’intersection de la perpenciculaire à l’axe optique passant par B′et de l’axe optique.

• On vérifie que l’image A′B′vérifie A′B′=γAB = 2,5 cm. Il s’agit d’une image virtuelle, droite et agrandie.
• On vérifie que l’objet AB est situé 1,6 cm devant la lentille. Il s’agit d’un objet réel.
-6
-5
-4
-3
-2
-1
0
1
2
3
4
5
1 cm
1 cm
O
A
B
F
F’
A’
B’