Cours# 7

1
IV.2.b. étude du magnétisme par diffraction des neutrons
IV.2.b.1. généralités sur la production de neutrons
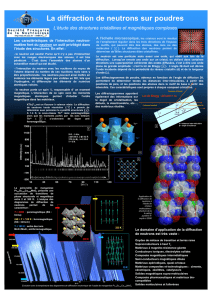
C’est une méthode indispensable pour la détermination des structures
magnétiques. En bien des points elle est analogue à la diffraction de rayons X. La
diffraction de neutrons peut être faite sur des solides mono ou polycristallins.
Limitation: disposer d’une pile atomique afin de produire un flux suffisant de
neutrons. (Les neutrons sont produits par fission atomique ) Il existe un
regroupement de laboratoires européens (France à Cadarache et Grenoble,
Allemagne à Munich et Karlsruhe, Grande-Bretagne,...). Ces laboratoires ont
ensemble pu élaborer un système qui génère quelque 1015 neutrons
thermiques/cm2/s (longueur d’onde entre 0,05 et 2 nm).
Un faisceau de neutrons est faible comparé à un faisceau de rayons X et
on doit travailler avec des faisceaux qui sont de 10 à 20 fois plus larges que les
faisceaux X si on veut obtenir des effets observables. La taille de l’échantillon doit
être de dimension correspondante →gros cristaux, qqs cm3de poudre.
IV.2.b.2. Diffraction des neutrons par les atomes
Les rayons X sont diffractés essentiellement par les ēpériphériques, les neutrons
sont diffractés essentiellement par les noyaux. Les neutrons possèdent également
un moment magnétique de spin analogue à celui de l’électron.
L’interaction entre ce moment magnétique et le moment magnétique des atomes
d’une substance produit les effets suivants :
- si les moments magnétiques atomiques sont orientés au hasard, il se produit une
diffraction incohérente qui n’est donc pas intéressante.
- si les moments magnétiques atomiques sont régulièrement arrangés, les
interactions sont toutes de même sens et on observe des angles θd’origine
magnétique. De la valeur de ces angles, on peut déduire l’orientation des moments
magnétiques à l’intérieur de la maille.
-la valeur des intensités des contributions magnétiques renseigneront sur la valeur
des mmts magnétiques.
Ainsi sur un diagramme de diffraction des neutrons, on obtient un diagramme
correspondant à la structure cristalline auquel se superpose un diagramme
correspondant à la structure magnétique.

2
IV.2.b.3. exemples de structures magnétiques
α) paramagnétisme
Il n’y a pas d’ordre à longue distance, il n’y aura donc aucune diffraction
cohérente, les contributions magnétiques sont diluées dans le fond continu.
cristal paramagnétique.
β) ferromagnétisme
Les raies de diffraction d’origine magnétique se superposent aux raies d’origine
nucléaire →la maille magnétique est identique à la maille cristalline.
Cristal ferromagnétique.
35ZrZn2630Cu2MnAl628Ni
336CrTe386CrO1388Co
318MnAs292Gd1043Fe
Tc (K)SolidesTc (K)SolidesTc (K)Solides

3
γ) antiferromagnétisme
Dans les solides antiferromagnétiques, à basses températures on peut voir qu’à la
structure cristalline s’ajoute une structure magnétique de paramètres de maille
différents, par ex. doublement selon l’un des axe, ……pour les oxydes de type
NaCl, tels MnO, FeO ou NiO on observe une déformation quadratique .
Orientation des spins
dans un cristal antiferromagnétique.
320
307
TN(K)
-580LaCrO3
-2000525NiO-690
403
MnTe
-485Cr2O3
-570198FeO-610122MnO
θp (K)
Solides
θp (K)
TN(K)Solides
θp (K)
TN(K)Solides
IV.3. domaines magnétiques et hystérésis
IV.3.a. définitions
Aux T° inférieures à TC, un matériau ferro ou ferrimagnétique est divisé en
volumes élémentaires appelés domaines magnétiques. Dans chacun de ces
domaines, l’aimantation est maximale donc égale à Ms (σs ) et tous les mmts
magnétiques atomiques sont orientés dans le même sens. Ces domaines sont
séparés par des parois appelés parois de Block. Comme l’orientation des mmts
magnétiques varie d’un domaine à l’autre, le changement d’orientation à lieu au
voisinage ou à l’intérieur des parois de Block.

4
A l’échelle macroscopique, un matériau renferme un très grand nombre de
domaines et a une aimantation M égale à la somme vectorielle de ces domaines.
Dans une substance non aimanté, cette somme est nulle. L’aimantation des
matériaux ferro ou ferrimagnétiques n’est pas proportionnelle à l’intensité du chp
appliqué, plus exactement elle ne lui est proportionnelle que pour les très faibles
valeurs de H. On suit la variation de l’aimantation en fonction du chp appliqué M =
f(H) cette courbe s’appelle la courbe d’aimantation.
courbe de première aimantation M=f(H)
Cycle d’hystérésis
Selon la forme et les dimensions du cycle d’hystérésis,on distingue deux
types de matériau : les mat magn doux et les mat magn durs.
IV.3.b. matériaux magnétiques doux
L’aire limitée par la boucle d’hystérésis représente l’E associée à chaque cycle
d’aimantation-désaimantation, l’E est dissipée sous forme de chaleur. Les mat
magn doux servent à fabriquer des appareils qui comme les transformateurs, qui
canalisent les chps magnétiques alternatifs sans perte importante d’E. L’aire de
leur courbe doit donc être la plus petite possible, cad avoir une grande
perméabilité initiale et un chp coercitif faible, ainsi il atteindra son aimantation à
saturation pour une valeur faible de chp appliqué.

5
Tableau représentatif de qqs composés ferromagnétiques doux
350.3665036NiFe2O4-52ZnFe2O4
Ferroxcube B
400.331400
48MnFe2O4-
52ZnFe2O4
Ferroxcube A
-0.875000
79Ni-15Fe-5Mo-
0.5Mn
Superpermalloy
1201.6250055Fe-45NiPermalloy 45
40
2.01140097 Fe-3SiFer-silicium
270
2.1415099.95 Fefer
E par cycle
(J /m3)
σs (T)
µiComposition
IV.3.c. matériaux magnétiques durs
Ils servent à fabriquer des aimants permanents, le chp magn q’ils engendrent, doit
rester stable dans le tps. Un mater magn dur présentera les caractéristiques
suivantes : aimantation à saturation élevée, forte aimantation rémanente et fort chp
coercitif. On définit également le facteur de mérite (B.H)max (SI) ou (M.H)max
(cgs)* qui correspond à la valeur maximale du produit M par H calculé dans le
deuxième quadrant du cycle d’hystérésis. Plus ce facteur de mérite est grand plus
le matériau est classé comme dur.
* le facteur de mérite s’exprime :
en kJ/m3(SI) ou
en MG.Oe (106Gauss. Oersted) ;
1 MG.Oe = 7.96 kJ/m3.