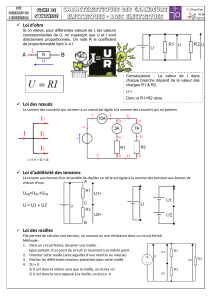
Phonons

I COORDONNEES NORMALES DU CRISTAL: 2
I.1 PREMIERS DEVELOPPEMENTS 2
I.2 ENERGIE CINETIQUE ; COORDONNEES GENERALISEES: 3
I.3 ENERGIE POTENTIELLE ; MATRICE DYNAMIQUE: 3
I.4 PROPRIETES DE LA MATRICE DYNAMIQUE ; COORDONNEES NORMALES: 4
I.4.1 ENERGIE CINETIQUE: 4
I.4.2 ENERGIE POTENTIELLE: 4
I.5 EQUATIONS DU MOUVEMENT 5
II RELATIONS DE DISPERSION ; BRANCHES ACOUSTIQUES ET BRANCHES
OPTIQUES 5
II.1 CHAINE LINEAIRE A UN ATOME PAR MAILLE ; INTERACTION ENTRE PLUS PROCHES
VOISINS: 5
II.2 CHAINE LINEAIRE A UN ATOME PAR MAILLE ; INTERACTION AVEC TOUS LES VOISINS 6
CHAINE LINEAIRE A DEUX ATOMES PAR MAILLE ; INTERACTIONS ENTRE PLUS PROCHES VOISINS: 6
II.4 DENOMBREMENT DES BRANCHES ACOUSTIQUES ; CAS GENERAL: 8
II.5 POLARISATION DES DIFFERENTS MODES 9
III EXEMPLES DE RELATIONS DE DISPERSIONS 10
III.1 PHONONS ACOUSTIQUES AUX GRANDES LONGUEURS D’ONDE DANS LES METAUX 10
III.2 PHONONS OPTIQUES DANS LES CRISTAUX IONIQUES 11
III.2.1 EQUATIONS DU MOUVEMENT: 11
III.2.2 POLARISABILITE
(
)
ω
α
12
III.2.3 CONSTANTE DIELECTRIQUE 12
III.2.4 RELATIONS DE DISPERSION 13
IV DETERMINATION EXPERIMENTALE DES RELATIONS DE DISPERSION DE
PHONONS 14
IV.1 REMARQUES PRELIMINAIRES 14
IV.2 CAS DES NEUTRONS 15
IV.3 CAS DES PHOTONS 15
V QUANTIFICATION DES MODES DE PHONONS 16
V.1 EXPRESSION DES COORDONNEES NORMALES EN FONCTION DES COORDONNEES
"NATURELLES" 16
V.2 TRANSPOSITION EN MECANIQUE QUANTIQUE ; COMMUTATEURS 17
V.3 HAMILTONIEN ET SOLUTION DU PROBLEME 17

Phonons
On considère dans tous ce chapitre le cas général d'un cristal de dimension contenant
0
latomes par maille élémentaire. Cette maille élémentaire sera repérée par sa position
R
r
dans
le cristal, et on notera
(
)
tu lR,
r
r
de coordonnées
(
)
α ,,lR
ur le déplacement du lième atome de la
maille élémentaire située en
R
r
.
I Coordonnées normales du cristal:
I.1 Premiers développements
Notons le potentiel d’interaction entre les atomes par
Φ
. On effectue ici l’approximation
harmonique, c’est-à-dire que l'on va faire un développement limité de ce potentiel au second
ordre en
α ,,lR
ur.
Par ailleurs, la position
(
)
[
]
0
,,1..,0 lBRlRu lR ×∈∀=
r
r
r
r est une position stable, c'est-à-dire
que
Φ
s'écrit dans cette approximation:
(1)
(
)
∑−Γ+Φ=Φ
’,’,’ ,, ’,’,’,,
,,’,’0 ’
2
1
α
ααα
αα
lR lR lRlR
ll uuRR
r
r
rr
r
r
Afin d'alléger les notations, on va introduire un nouvel indice
ν
correspondant aux couple
d'indices
(
)
α
,l. On aura donc
[
]
dl0 ,1
∈
ν
.
On a par ailleurs les propriétés suivantes:
-
(
)
(
)
’’ ,’’, RRRR
r
r
r
r
−Γ=−Γ
νννν
- si on considère qu'il y a
α
N mailles dans une direction, avec donc NN =
∏
αα
, alors
les conditions aux limites périodiques imposent lRlRNR uu ,, rrr
r
r
=
+
αα
.
On décompose alors
ν ,R
ur
r
en série de Fourier:
(2) ∑
∈
=PZBk
Rki
k
Reu
N
ur
r
r
rr .
,
,1
ν
ν
Comme
ν ,R
ur est réel, on a immédiatement
(3)
(
)
*
,, νν kk uu rr
=
− et enfin, d'après les propriétés des séries de Fourier:
(4) ∑
∈
−
=..
.
,
,1
BRR
Rki
R
keu
N
ur
r
r
rr
ν
ν

I.2 Energie cinétique ; coordonnées généralisées:
L'énergie cinétique totale s'écrit alors, avec ces notations:
(5) ∑ ∑ ∑ ==
νννν ,
2
,
2
,2
1
2
1
R R
R
o
l
R
o
luMuMT r r
rr
Or d'après le théorème de Parseval:
(6) ∑∑∑ − == k
vk
o
vk
o
k
k
o
R
R
ouuuu r
rr
r
r
r
r,,
2
,
2
, νν
On obtient donc:
(7) ∑−
=
ν ,
,,
2
1
k
vk
o
vk
o
luuMT r
rr
On peut alors introduire une coordonnée généralisée vk
l
kuMQ ,, rr = ν
, et on a:
(8) ∑−
=
νν ,,,
2
1
kk
o
vk
oQQT r
rr
I.3 Energie potentielle ; matrice dynamique:
Si on exprime l'énergie potentielle (1) en fonction de la transformée de Fourier du
déplacement, on obtient:
(9)
(
)
[ ]
∑ ∑ +
−Γ+Φ=Φ ’,’,, ’,
’’.
’,’,
’0 1
’
2
1
νν νν
νν
RR kk
RkRki
kk euu
N
RR
rr rr
r
r
r
r
rr
r
r
, ce qui se réécrit:
(10)
(
)
[ ]
∑ ∑ +
−Γ+Φ=Φ ’,’,, ’,
’’..
,’
’,’,
0’
1
2
1
νν νν
νν
kk RR
RkRki
kk eRR
N
uu
rr rr
r
r
r
r
rr
r
r
La somme sur les ’,RR
r
r
se réécrit, en posant
R
R
R
r
r
r
−
=
’
"
:
(11)
(
)
( )
(
)
( )
∑ ∑∑ +−−+ Γ=Γ " ’
’.
,’
",’
".’’
’1
""
1
R R
RkkiRki
RR
RkiRkki e
N
eReeR
Nr r
r
rr
r
r
rr
r
r
r
rr
r
r
νννν
.
La première somme correspond exactement à la transformée de Fourier de la fonction
(
)
R
r
νν ,’
Γ, et la seconde vaut ’, kk rr −
δ
, ce qui implique finalement:
(12)
(
)
∑Γ+Φ=Φ −
’,, ’
’,,
02
1
νν νν
νν
kkk kuu
r
rr
r
On introduit alors les coordonnées généralisées ainsi que la grandeur
(
)
(
)
k
MM
kD
ll
r
r
’
’
’1 νννν
Γ= , et on obtient:
(13)
(
)
∑−
+Φ=Φ ’,, ’,
’,,
02
1
νν νν
νν
kkk kDQQ
r
rr
r
La matrice dldl .. 00
×
(
)
’,
’,
νν
νν
DD
=
est appelée matrice dynamique. L'énergie potentielle
s'écrit alors sous forme condensée:
(14) ∑−
+Φ=Φ kkk QDQ
r
rr
r
r
2
1
0.

I.4 Propriétés de la matrice dynamique ; coordonnées normales:
D est hermitique. En effet, on a:
(15)
(
)
(
)
(
)
(
)
(
)
(
)
*
’’
.
’
.
’
.
’’ νννννννννννν
Γ=−Γ=Γ=−Γ=Γ=Γ
∑
∑
∑
−− keReReRk R Rki
R
Rki
R
Rki
r
r
r
r
r
r
r
r
r
r
r
r
r
r
,
ce qui implique que
(
)
(
)
[
]
*
’’ kDkD
r
r
νννν
=
Ceci implique que l’on va pouvoir diagonaliser D, et que ces valeurs propres vont être
réelles.
Soit
(
)
s
k
r
ξ
les valeurs propres de D, avec
[
]
dls 0 ,1
∈
, et
(
)
s
k
er
r
les vecteurs propres associés,
tels que
(
)
(
)
[
]
(
)
(
)
’,
’’ .*. ss s
k
s
k
s
k
s
keeee
δ == −rrrr
r
r
r
r
.
Les valeurs propres étant réelles, on a immédiatement
(
)
(
)
s
k
s
krr −
= ξξ
.
On peut alors décomposer les coordonnée généralisées sur la base des vecteurs propres de
D, ce qui s'écrit:
(16)
(
)
[
]
(
)
(
)
∑
== s
s
kskkk etqQtQ rrrr
r
r
,, ν
Les sk q,
rsont appelées coordonnées normales.
On peut alors réécrire l'énergie cinétique et l'énergie potentielle à l'aide de ces
coordonnées:
I.4.1 Energie cinétique:
(17)
( ) ( ) ( ) ( )
∑ ∑∑∑ −
−
−
−− === ’,,
’,,
,,
’,,,
’,,
,,
,,, .
2
1
.
2
1
2
1
ssk
s
k
s
k
sk
o
sk
o
ssk
s
k
s
k
sk
o
sk
o
kk
o
k
oeeqqeeqqQQT r
rr
rr
r
rr
rr
r
rr
ννν
ννν ννν
.
Or on a
(
)
(
)
(
)
(
)
∑
== −−
ν
δ
νν
’,
’’,, .. ss s
k
s
k
s
k
s
keeee rrrr
r
r
, ce qui donne:
(18) ∑−
=sk sk
o
sk
oqqT
,,,
2
1
r
rr
I.4.2 Energie potentielle:
On a:
(19)
( ) ( )
∑ ∑∑ 
+Φ=+Φ=Φ −−
−
−ks
s
k
s
k
sk
k
kkk eqQQDQ r
rrr
r
rr
r
rrr
ξ
,00 ., ce qui donne:
(20)
(
)
∑
−
+Φ=Φ sk sksk
s
kqq
,,,
0r
rrr
ξ
Remarques:
→1l'équation (20) peut se réécrire
( )
∑
+Φ=Φ sk
s
ksk
q
,
2
,
0r
rr
ξ . Or puisque l'état 0
,
=
ks
qr est
une position d'équilibre stable, on a forcément
(
)
(
)
sk
s
k,0
r
r∀≥
ξ
.

→2 la dimensionalité de
ξ
est donnée par:
[ ]
[ ]
2
2
22
.
11 −
−==Γ= T
L
TML
MM
ξ .
On va donc poser dans toute la suite
(
)
2,sk s
krr
ωξ =
I.5 Equations du mouvement
Le lagrangien du système s'écrit:
(21) 0
,,,
2,
,,
2
1Φ−
−=Φ−= ∑−
sk sksksk
sk
o
sk
oqqqqTL r
rrr
rr
ω
On en déduit les équations du mouvement par
sk
sk
oqL
q
L
dt
d
,
,
r
r∂
∂
=
∂
∂
, ce qui donne:
(22) 0
,
2,
,=+ sksk sk
oo qq rr
r
ω
On obtient donc, grâce aux coordonnées normales, dNl0équations d’oscillateurs
harmoniques indépendants.
La solution de ces équations est donnée par:
(23) ti
sk
ti
sksk sksk eBeAq ,, ,,, rrr
ωω −
+=
Or on a
(
)
*
,, sksk qq rr
=
−, ce qui implique que
(
)
*
,, sksk AB rr
=
−.
Les déplacements "réels" seront obtenus à partir des q par:
(24)
( ) ( )
( )
∑ ∑
∈
=PZBk s
Rkis
ksk
l
Reetq
NM
tu r
r
r
rrr .
,,
,1
ν
ν
Pour une valeur de k
r
, on a donc dl0 relations de dispersions, ce qui signifie que pour les
phonons, qui sont les modes de vibration du cristal, on aura dl0branches de dispersion,
éventuellement dégénérées.
II Relations de dispersion ; branches acoustiques et branches optiques
II.1 Chaîne linéaire à un atome par maille ; interaction entre plus proches voisins:
Ceci correspond à une énergie potentielle:
(25)
( )
∑−+Φ=Φ +
nnn uuC 2
10 2
1
Pour reprendre les notations du paragraphe précédent, on écrit:
(26) ∑+
−+Φ=Φ nnnn uCuCu 1
2
02
2
1, ce qui implique que
Γ
n'est non nulle que pour
trois valeurs de k:
(27)
(
)
C20 =Γ et
(
)
(
)
Caa −=−Γ=Γ