A- Contrôle de connaissances : Le cyclotron (8,5 points)

2IMRT, Devoir surveillé, 19 03 2012
A- Contrôle de connaissances : Le cyclotron (8,5 points)
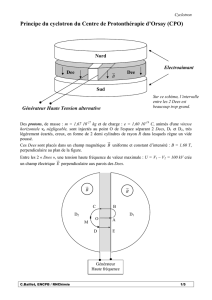
Dans l'accélérateur ci-contre, des protons de vitesse initiale négligeable sont injectés
en un point O situé sur l'une des pièces métalliques creuses, puis suivent le trajet
O, A, B, C, D, E etc ...
Chacune des séries de propositions 1, 2, 3, … contient une seule
affirmation vraie. Recopier la lettre correspondant à l'affirmation vraie
sur la copie et la justifier brièvement si cela est demandé.
1. Le champ électrique
E
entre les dees :
a) ne change pas de sens
b) a la direction et le sens du vecteur vitesse du proton entre les dees (VRAI)
c) est perpendiculaire au vecteur vitesse du proton entre les dees
d) s’annule quand le proton pénètre dans un dee
Comme le mouvement est rectiligne accéléré entre les dees, le vecteur vitesse
v
a la direction et le
sens du vecteur accélération
a
et donc aussi de la force électrique
F
= m
a
(2ème loi de Newton) et
du champ électrique
E
=
F
/q car la charge q des protons est positive
2. La tension VD1-VD2 entre les dees :
a) conserve la même valeur et le même signe,
b) change de signe et conserve la même valeur,
c) change de valeur et de signe, (VRAI)
d) change de valeur et garde le même signe.
3. Dans chacun des deux « dees », la trajectoire du proton est un demi-cercle parcouru :
a) à vitesse constante, (VRAI)
b) avec une vitesse dont la valeur varie sinusoïdalement.
c) avec une vitesse croissante,
4. Entre les deux « dees », le proton décrit une trajectoire rectiligne avec une vitesse dont la valeur:
a) est constante
b) est croissante, (VRAI)
c) varie de façon sinusoïdale.
5. Le rayon de courbure de la trajectoire du proton :
a) augmente avec la valeur du champ magnétique
B
,
b) augmente avec la vitesse à l'entrée des « dees », (VRAI)
c) ne dépend pas de l'énergie cinétique du proton à son entrée dans un « dee »
6. La durée du parcours d'un proton dans un dee:
a) dépend de la vitesse d'entrée dans le dee,
b) dépend de la durée du trajet entre les deux dees
c) dépend de la période de la tension sinusoïdale entre les dees,
d) dépend de la valeur de
B
(VRAI) (justifier l'affirmation)
La durée du parcours dans un dee vaut une demi-période de rotation T dans le champ
magnétique
B
; cette rotation s’effectue à vitesse constante v le long d’une trajectoire circulaire
de rayon R, donc v =
longueur trajectoire
durée rotation =
2 R
T
et T =
2 R
v
; comme R =
mv
|q| B
l’expression de la période devient T =
2 .mv
v.|q | B
=
2 m
|q| B
; expression qui ne dépend que de B
7. L’énergie cinétique du proton,
a) augmente seulement dans les « dees »
b) augmente dans les « dees » et entre les « dees »
c) augmente seulement entre les « dees » (VRAI)
d) augmente au passage de D1à D2puis diminue au passage suivant de D2à D1
C
O
D
B
A
E
D
1
D
2
B
B

8. Un proton sort de l’accélérateur avec une énergie cinétique égale à 500 MeV. La tension entre
les « dees » ayant une amplitude de 10kV, le nombre de tours effectués par le proton est :
a) N = 250 ; b) N = 50 000 ; c) N = 25 000 (justifier l'affirmation)
à chaque passage entre les dees, l’énergie cinétique du proton augmente de W = |q|Umax donc le
nombre de passages entre les dees est Np= (Ec(finale) –EC(initiale))/W ≈ E
c(finale)/W ;
soit : Np= 500 MeV/(10 keV) = 500 x106/(10 x103) = 50 000 et comme il y a deux passages par
tours le nombre de tours est N = Np/2 = 25 000
9. Un proton sortant d’un cyclotronet dirigé vers une cible de molybdène 10042 Mo peut provoquer
la réaction nucléaire Mo(p,2n)X où X est un radionucléide très utilisé en médecine nucléaire :
a) 9039Y ; b) 9741Nb ; c) 99m43Tc (VRAI) (justifier l'affirmation)
10042 Mo+11p99m43Tc + 2 10n ; conservation des nucléons : 100+1 = 99 + 2 x1
conservation de la charge : 42 + 1 = 43 + 0
(résultat obtenu récemment par des chercheurs canadiens )
B- Spectrographe de masse (11,5 points)
Données :
charge électrique élémentaire : e = 1,60 x10-19C
masse d’un nucléon: mn= 1,67 x10-27 kg
Le poids d’un ion peut être négligé devant les autres forces exercées sur l’ion.
La masse d’un ion est assimilable à la masse totale des nucléons de son noyau.
La vitesse d’un ion est suffisamment faible pour pouvoir appliquer les lois de la mécanique classique.
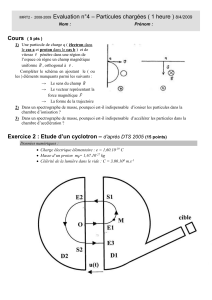
1. Une chambre d'ionisation produit un mélange d’ions
zinc 68Zn2+ et XZn2+. Ces ions sont accélérés dans le vide
entre deux plaques parallèles P1et P2, distantes de
d = 2,5 cm et soumises à une tension U = 1000 V.
1.1 Indiquer les polarités des plaques et le signe de la
différence de potentiel VP1-VP2.
ions positifs accélérés de la plaque positive (P1) à la plaque
négative (P2) donc VP1 > VP2 et VP1-VP2 > 0
1.2 Indiquer la direction et le sens du vecteur champ électrique
E
entre les plaques puis calculer sa valeur.
Vecteur champ électrique
E
perpendiculaire aux plaques,
dirigé vers la plaque de plus faible potentiel (P2) et de valeur
E = U/d = 1000/0,025 = 4,0 x104V.m-1 = 40 kV.m-1
2. Établir l'expression de la vitesse v1d’un ion
68Zn2+ au passage en S en négligeant
leur vitesse en O puis calculer v1avec trois chiffres significatifs.
On applique le théorème de l’énergie cinétique à un ion
68Zn2+ de masse m1= 68mnet de charge q= 2e
soumis à la tension VP1-VP2 entre le point d’émission O avec une vitesse nulle et le pointde passage S
avec la vitesse v1dans le référentiel terrestre supposé galiléen :
EC(S) –EC(O) = q(VP1-VP2) ; ½ m1v12–0 = qU ; v1=
1
2qU
m
=
n
4eU
68m
; soit v1=
n
eU
17m
application numérique : v1=
19
27
1,60 10 1000
17 1,67 10 = 7,51 x 104m.s-1
3. Montrer qu’un ion
XZn2+ passe en S avec la vitesse v2vérifiant la relation :
x
68
v
v
1
2
OS
(P1) (P2)
I1
I2
Chambre
d’ionisation
B
M+
F
v

le même raisonnement appliqué à l’ion
XZn2de masse m2= Xmnet de même charge q conduit à :
½ m2v22–0 = qU donc ½ m2v22=½m1v12; m2v22= m1v12;  
2
n
2 1
1 2
68m
v m
v m
n
X m
,d’où:
2
1
v
68
v X
4. Après leur passage en S, les ions pénètrent dans une enceinte où règne un champ magnétique
uniforme
B
, orthogonal au plan de figure. Les ions décrivent alors des trajectoires curvilignes situées dans le
plan de figure et représentées en traits hachurés.
4.1. Préciser sur le schéma le sens du vecteur
B
sachant que les ions 68Zn2+ arrivent en l1et les ions XZn2+
arrivent en I2.
4.2 Exprimer la force magnétique
F
exercée sur l’ion
68Zn2+ de vitesse
v
et représenter les vecteurs
F
et
v
au point M.
Force de Lorentz
F
= q
v B
5. Le mouvement d'un ion de masse m, de charge q et de vitesse v est uniforme et circulaire de rayon :
R =
mv
|q|B
5.1 Le rayon de la trajectoire de l’ion
68Zn2+ vaut R1= 26,6 cm. Calculer la valeur B du champ magnétique.
L’ion
68Zn2+ décrit une trajectoire de rayon R1avec la vitesse v1donc
B=
1
1
mv
|q|R
=
n 1
1
68m v
2eR =
n 1
1
34m v
eR =
-27 4
-19
34×1,67×10 ×7,51×10
1,60×10 ×0,266 = 0,100 T = 100 mT
5.2 Montrer qu’un ion
XZn2+ décrit une trajectoire de rayon R2tel que : 1
2
R
R=68
X
(Utiliser la relation 1.4)
L’ion
68Zn2+ décrit une trajectoire de rayon R2avec la vitesse v2donc
2
1
R
R
=
2 2
1 1
m v
|q|B
m v
|q|B
=
2 2
1 1
m v
m v
=
2 2
1 1
m v
m v
=n
X m
n
68m
68
×
X
=
X
68
6. La distance entre les points d’arrivées des ions est I1I2= 8 mm.
6.1 Que représentent les distances SI1et SI2? Déduire la valeur du rayon R2
Les distances SI1et SI2sont les diamètres des trajectoires des ions 68Zn2+ etXZn2+ respectivement
SI2= SI1+ I1I2donc 2R2= 2R1+ I1I2et R2= R1+
1 2
I I
2
= 26,6 +
0,8
2
= 27,0 cm
6.2 Identifier l’isotope
XZn2+.
2
1
R
R
2
=
X
68
donc X = 68 2
1
R
R
2
=68x
2
27,0
26,6
≈ 70 ; il s’agit donc de l’isotope
70Zn2+