télécharger le cours - e

—————————————
1 sur 11
Voir est un phénomène complexe qui implique une succession d’événement qui permettent de
détecter, localiser et identifier un objet éclairé par une source de lumière.
L’œil est l’organe de la vision, il permet d’abord de focaliser le stimulus lumineux sur sa partie
photosensible qui est la rétine.
Ceci est régit par les lois de l’optique géométrique.
Certaines cellules de la rétine qu’on appelle des photorécepteurs (sensibles aux photons) vont
transformer cette information lumineuse en signal électrique.
! C’est la photo transduction
Puis le réseau neuronal rétinien va trier et comprimer l’information avant de la transmettre au
cerveau où elle sera analysée. Ce cheminement de l’information constitue la chaîne visuelle.
La lumière est une onde électromagnétique qui peut se propager en l’absence de milieu matériel
(c’est à dire dans le vide). Mais Planck et Einstein en 1906 ont aussi démontré que la lumière
pouvait être définie comme un flux de photons : c’est ce qu’on appelle la théorie corpusculaire.
Cette dualité entre onde/flux photon s’appelle : la dualité onde corpuscule.
La lumière est à la fois une onde et un corpuscule !
La formation des images par les systèmes optiques peut être décrite par une approche géométrique,
cette approche s’appelle l’optique géométrique.
L’optique géométrique permet d’étudier le comportement des rayons lumineux entre 2 milieux
d’indices de réfraction différents.
L’axe optique est orienté dans le sens de propagation de la lumière.
A) Les dioptres
1) Définition
Un dioptre est la surface séparant 2 milieux homogènes et transparents d’indices de réfraction
différents.
UE3
Optique géométrique

—————————————
2 sur 11
• Par convention, on appelle n1 l’indice de réfraction du milieu où se situent les rayons
lumineux incident.
• On appellera n2 l’indice de réfraction du milieu où se situent les rayons lumineux réfractés.
• Le point O qui coupe l’axe optique constitue le sommet du dioptre.
n = indice de réfraction du milieu (sans dimension).
c = vitesse de la lumière dans le vide.
v = vitesse de la lumière dans le milieu considéré.
𝒏!=!
𝒄
𝒗!
n air = 1
n verre = 1,5
2) Stigmatisme
Un dioptre est dit stigmatique s’il donne d’un objet ponctuel une image ponctuelle (l’image d’un
point est un point).
Les points image et objet sont dits conjugués.
3) Dioptre sphérique
C’est un dioptre dont la surface de séparation va être un élément de sphère.
Toutes les distances sont orientées positivement dans le sens de propagation de la lumière. Et leur
origine est le sommet du dioptre O.
Il existe un segment OC orienté, qu’on appelle rayon de courbure du dioptre sphérique.
4) Approximation de Gauss
Un système parfait est un système stigmatique, mais ce système « parfait » n’est jamais réalisé,
d’où la notion de stigmatisme approchée.
Une somme de 3 conditions constitue l’approximation de Gauss.
Quand les 3 conditions de l’approximation de Gauss sont respectées, le système peut être dit
stigmatique.

—————————————
3 sur 11
5) Relation de conjugaison
Les rayons issus de A1 vont couper l’axe optique en un point A2 après traversée du dioptre.
Les points A1 et A2 sont dits conjugués, et leurs points sont liés par une relation de conjugaison.
−!
𝒏𝟏
𝑶𝑨𝟏
+!
𝒏𝟐
𝑶𝑨𝟐
=!
𝒏𝟐 −𝒏𝟏
𝑶𝑪
6) Puissance (D)
La puissance (D) est définie par la relation :
𝑫=!
𝒏𝟐 −𝒏𝟏
𝑶𝑪
D : puissance en dioptries (= m-1)
Les distances sont toujours orientées et exprimées en mètre.
7) Proximité
La proximité d’un point image ou objet est définie sur l’axe optique comme l’inverse de la distance
orientée (en m) entre le sommet du dioptre et le point considéré.
Elle s’exprime en m-1.
La dioptrie peut s’utiliser pour exprimer la puissance d’un dioptre mais aussi la proximité d’un
point objet ou image.

—————————————
4 sur 11
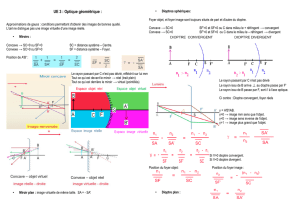
B) Dioptre convergent et divergent
1) Dioptre convergent
• Distance focale image :
Dans un dioptre sphérique convergent, si un faisceau de rayons lumineux incidents arrive
parallèlement à l’axe optique, les rayons lumineux émergent de ce dioptre en convergeant (donc en
se rapprochant de l’axe optique).
Le point d’intersection avec l’axe optique est appelé point focal image = foyer principal image
qui est construit seulement si les rayons arrivent parallèles à l’axe optique.
La distance orientée OFı s’appelle la distance orientée focale image.
Le foyer image est réel.
Distance focale image 𝐎𝐅! est > 0, exprimée en mètres.
• Distance focale objet
L’objet qui donne une image à l’infini sur l’axe optique est situé au point focal objet Fo de cet axe
= foyer principal objet. Cet objet est réel car situé sur l’axe optique.
La distance focale objet 𝑶𝑭𝒐 est < 0.
Dioptre convergent en résumé :
• D > 0
• Foyer image principal est réel
• Foyer objet est réel
• Distance focale image > 0
• Distance focale objet < 0.

—————————————
5 sur 11
2) Dioptre divergent
Un dioptre sphérique divergent se caractérise par :
• D < 0,
• Foyer image est virtuel,
• Foyer objet est virtuel,
• Distance focale image < 0,
• Distance focale objet > 0.
3) Conditions de vision nette
Il doit y avoir simultanément : Conditions dioptriques optimales + Intégrité de la chaine
visuelle.
o Conditions Dioptriques optimales : (ne permettent pas de dire si le sujet verra nettement -
ex : infection rétine…)
1) Le dioptre doit être stigmatique,
2) Image formée sur la rétine,
3) Convergence normale des 2 yeux.
o Intégrité de la chaine visuelle : rétine, voies visuelles, cortex.
4) Grandissement
Cas d’un dioptre sphérique convergent :
3 rayons lumineux permettent d’obtenir l’image d’un objet quelconque après traversée d’un dioptre
sphérique :
a) Le rayon lumineux qui passe par le centre d’un dioptre n’est pas dévié.
b) Le rayon parallèle à l’axe principal passe par le point focal image FI après la
traversée du dioptre.
c) Le rayon qui passe par le point focal objet Fo sort du dioptre parallèlement à l’axe
principal.
Cette construction permet de définir 3 notions :
1) 2 de ces 3 rayons suffisent pour construire une image
2) L’objet est orienté de façon opposée à l’image ! l’image est inversée par rapport à
l’objet.
3) L’image est plus petite que l’objet. Elles ne font pas la même taille.
" Notion de grandissement, permet de définir le rapport entre l’image et l’objet.
𝛄=
𝐀𝟐𝐁𝟐
𝐀𝟏𝐁𝟏
=!
𝐧𝟏
𝐧𝟐!×!
𝐎𝐀𝟐
𝐎𝐀𝟏
Le grandissement sera une valeur négative.