Goubau Martin Le losange Leçon n° Prénom : Date : Sujet : Math

Goubau Martin Le losange Leçon n°
Sujet : Math : Géométrie : La famille des losanges.
Ecole : Pavillon du tilleul
Classe : 4/5/6ème primaire.
Nombre d’enfants : 17.
Durée : 2x 50 minutes
Objectifs :
- A la fin de la leçon, les enfants seront capables de reconnaitre un losange, d’en donner
la définition et les caractéristiques.
A la fin de la leçon, les enfants auront découvert les différents axes de symétrie et
connaitrons les formules d’aires et de périmètre qu’ils mettront en pratique lors
d’exercices.
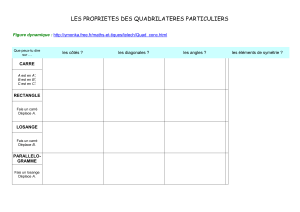
Compétences :
 Connaitre et énoncer les propriétés de côtés et d’angles utiles dans les constructions de
quadrilatères et de triangles.
 Connaitre et énoncer les propriétés des diagonales d’un quadrilatère.
 Dans un contexte de pliage, de découpage, de pavage et de reproduction de dessins,
relever la présence de régularités.
 Reconnaitre la présence d’un axe de symétrie.
Programme des études :

Goubau Martin Le losange Leçon n°
Fiche matière :
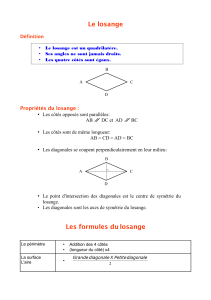
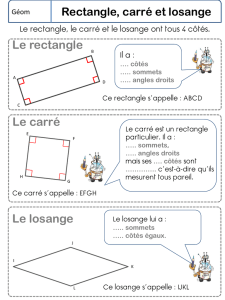
Le losange est un quadrilatère dont
les quatre côtés sont de même
longueur.
ses diagonales se coupent en leur milieu.
ses côtés opposés sont parallèles et de même
longueur.
les angles opposés sont égaux.
ses diagonales sont perpendiculaires.
ses médianes se coupent en leur milieu et sont
isométriques .
 les diagonales sont axes de symétrie.
 le point d'intersection des diagonales est centre de symétrie.
 le losange est un parallélogramme.
 Le losange est un trapèze.
 Pour calculer son périmètre on utilise la formule : 4xC
 Pour calculer son aire on utilise la formule : (Dxd) : 2

Goubau Martin Le losange Leçon n°
1. Initiation :
Nous observons le blason de la commune de Forest. Que constatons-nous ?
- Le blason est un quadrilatère.
- Le blason a les quatre côtés de même longueur.
- Le blason est divisé en deux parties
- Le blason est divisé en deux parties par une ligne verticales. Les deux parties
forment des triangles isocèles aigus.
- Les quatre angles sont aigus.
- Le blason ressemble à un carré.
Je note au tableau toutes les observations des enfants.
Je demande si les enfants connaissent le nom de la figure géométrique qui est formée par le
blason.  Un losange.
Je distribue une feuille aux enfants sur laquelle se trouvent des losanges sur lesquels j’ai
ajouté les diagonales afin que l’on puisse observer les axes de symétrie …
2. Observations des diagonales :
- Elles se coupent en leur milieu.
- Elles sont perpendiculaires.
- Elles ne sont pas de même longueur.
3. Observation des angles :
Le losange a 4 angles dont la somme est égale à 360°. Les 2 angles opposés ont la même
amplitude. Le losange a une paire d’angles aigus qui sont opposés et une paire d’angles obtus
qui sont également opposés.
Les angles consécutifs sont supplémentaires. Donc, qu’ils valent 180°.
Le carré est un cas particulier qui a 4 angles droits.

Goubau Martin Le losange Leçon n°
Le périmètre :
La formule du périmètre d’un losange est : 4 x Coté
Exemple : Un losange de 2 cm de cotés aura un périmètre de 8 cm.
L’aire :
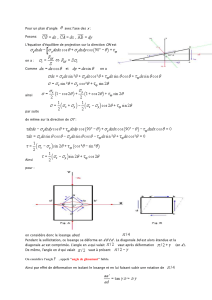
Comment trouver la formule d’air ?
Le losange est un demi-rectangle dont les dimensions sont D et d.
Donc, la formule du losange est D x d
2
L’aire d’un losange se calcule avec la formule
Exemple : Un losange ayant sa petite diagonale de 2 cm et la grande de 4 cm aura pour aire :
2 x 4 = 4 cm²
2
Pour que les enfants comprennent la formule du losange, j aurai découpé 2 losanges dans une
feuille et un des losanges, de couleur, sera divisé en 4 rectangle afin de pouvoir construire un
rectangle.
Instit demande aux enfants s’ils ont bien compris et distribue une feuille d’exercices sur le
périmètre et l’aire du losange.
D x d
2

Prénom : __________________
Date : ____________________
Le losange :
Exercices pour les 4èmes :
1. Quelle est la formule du périmètre du losange ? __________________
2. Quelle est la formule de l’aire du losange ? _______________________
3. Calculez le périmètre des losanges suivants :
4. Calculez l’aire des losanges suivants :
1
1)
2)
3)
2
3
1
2
3
1)
2)
3)