ϕ ρ ϕ ρ ρ ρ ϕ ρ

SCA 4622 : Dynamique de l’atmosphère
Eva Monteiro Page
1
Pratique 1
Approximation géostrophique
Quand le nombre de Rossby tend ver zéro, l’écoulement s’appelle géostrophique. Dans
l’écoulement géostrophique le vent est tel qu’il existe un équilibre horizontal entre la force de
gradient de pression et la force de Coriolis et, à la vertical, l’équilibre hydrostatique.
Les équations de mouvement dans le cas d’équilibre géostrophique sont :
12sin 0
12sin 0
10
pv
x
pu
y
pg
z
ϕ
ρ
ϕ
ρ
ρ
∂
−+Ω =
∂
∂
−−Ω =
∂
∂
−−=
∂
(1)
Tous les écoulements dont le nombre de Rossby est petit s’approchent de l’écoulement
géostrophique.
À partir de quelle valeur le nombre Rossby est assez petit pour admettre que le mouvement
est quasi-équilibre géostrophique?
En météorologie, l’écoulement est admis comme géostrophique quand le nombre de Rossby
est plus petit ou égal à 0,1. Ceci équivaut à l’acceptation d’une erreur de 10 % dans le calcul
de la vitesse du vent. Cette erreur de même ordre de grandeur que celle associée aux
incertitudes dans la mesure des variables météorologiques à l’échelle synoptique.
Le système d’équations (1) décrit l’approximation géostrophique appliquée aux systèmes
météorologiques aux latitudes moyennes.
En réalité, quelque soit l’écoulement, même s’il n’est pas géostrophique, il est possible de
définir un vent géostrophique, théorique, comme le vent qui crée une force de Coriolis qui
équilibre exactement le gradient de pression :
1,
1,2sin
g
g
p
ufy
p
vf
fx
ρ
ϕ
ρ
∂
=− ∂
∂
==Ω
∂
(2)
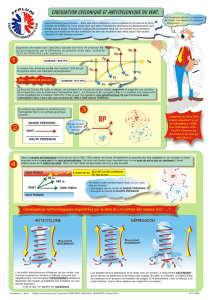
La figure 1 montre l’équilibre géostrophique dans le cas d’un gradient de pression
méridionale.

SCA 4622 : Dynamique de l’atmosphère
Eva Monteiro Page
2
Figure 1 : Équilibre géostrophique
Le vent géostrophique est proportionnel au gradient de pression. Si le gradient de pression
change dans l’espace et dans le temps, le vent géostrophique change.
Figure 2 : Vent géostrophique due à la différence de température entre deux masses d’air.
Figure 3 : Carte de pression au niveau de la surface montrant le vent et la pression aux stations.
L’approximation géostrophique nous aide à expliquer pourquoi les systèmes se déplacent de
l’ouest vers l’est (figure 2) Elle explique aussi le sens de l’écoulement observé autour de
centres de haute et de basse pression (figure 3).

SCA 4622 : Dynamique de l’atmosphère
Eva Monteiro Page
3
Pratique 1 : Analyse d’échelle
1) Calculez l’épaisseur de la couche atmosphérique délimitée par les niveaux de pression
1000 hPa et 700 hPa dans lle cas :
a) D’une masse d’air polaire (A) où la température moyenne est de -20 ˚C;
b) D’une masse d’air maritime tropicale (mT) où la température moyenne est de 20 ˚C.
2) Calculez le nombre de Rossby et le nombre de Reynolds pour chacun des phénomènes
décrits dans le tableau suivant, en sachant qu’ils sont observés à la latitude de ±45˚:
Type de système Échelle horizontale (L) Échelle verticale (H)
Front froid 50 km 1-2 jours
Tornade 100 m Minutes
Cumulus 1 km 10 minutes
a) Tirez des conclusions par rapport aux forces importantes dans la description du
mouvement de ces systèmes.
b) En quelles conditions les forces de viscosité sont importantes?
3) Supposez que les échelles qui figurent dans le tableau ci-dessus sont valides pour des
systèmes à n’importe quelle latitude.
a) Calculez le nombre de Rossby aux latitudes 0˚, 10˚, 30 ˚, 45˚, et 90˚.
b) À quelle(s) latitude(s) l’approximation géostrophique peut être appliquée et avec
quelle précision?
4) Quelles termes de l’équation horizontale de mouvement peuvent être négligés dans le cas
d’une dépression synoptique si on veut avoir une précision de :
a) 10 % ?
b) 1 % ?
c) 0,1 % ?
5) Les vents catabatiques sont des vents froids qui descendent des pentes sous l’action de la
gravité. On observe ce type de vent en Groenland (dévalant les pentes glacées de la calotte
polaire) et aussi, à une échelle plus petite sur les pentes des montagnes. Les échelles typiques
des vents catabatiques de Groenland sont : U = 10 m/s, L = 1000 km. Les échelles typiques
des vents catabatiques des montagnes sont U = 1 m/s et L = 1 km.
a) Calculer le nombre de Rossby des deux vents.
b) Discutez de l’importance relative de la force de Coriolis dans chacun des deux
écoulements.
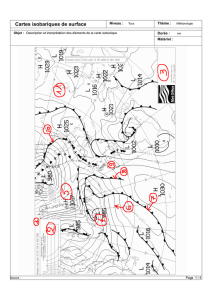
6) Faites une estimation des vitesses du vent géostrophique à Little Rock, Arkansas à 00 UTC,
le 15 février 2003 à la surface, à 700 mb, 500 mb et 300 mb, en utilisant les mesures des
stations des cartes de surface et d’altitude. Comparez le vent géostrophique à chaque niveau
avec la vitesse du vent mesurée.

SCA 4622 : Dynamique de l’atmosphère
Eva Monteiro Page
4

SCA 4622 : Dynamique de l’atmosphère
Eva Monteiro Page
5