Notion de calcul vectoriel

Université Joseph Fourier
Année universitaire 2005-2006
I- Calcul de la vitesse du vent en surface
On souhaite estimer la vitesse du vent au sol. On utilise pour cela soit des courbes
isobares à altitude constante, soit des courbes isohypses (exprimé en m au dessus de la
surface) à pression constante (altitude de la surface P=500hpa par exemple).
1) rappeler les hypothèses qui permettent d’écrire les équations du vent géostrophique
(ug, vg). Montrer qu’il résulte de ces hypothèses un équilibre entre force de Coriolis et gradient
de pression.
2) montrer gradzP = ρ.g.gradPz. (gradient de pression à z=cte est égale au gradient de z à
P=cte)
3) déduire les composantes du vent géostrophique.
4) Calculer le paramètre de Coriolis f.
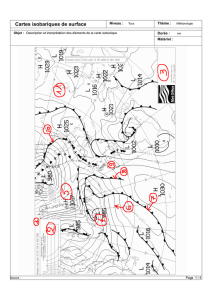
5) On donne la carte isohypse à 500 hPa du 19 février 2006 à 12h00. En utilisant 3 ou 4
isohypses (dont vous préciserez l’altitude), donner le vent géostrophique en m/s et en km/h, au
sud de Marseille.
6) on considère ensuite la carte du champ de pression en surface (carte isobares au sol) :
-Donner à partir de cette carte le vent géostrophique Vgs1 en m/s et en km/h, au sud de
Marseille en précisant les isobares utilisées et leurs interdistances
-déterminer, sur l’Europe de l’ouest, l’endroit où le vent vous semble devoir être le plus
fort. - évaluer le vent géostrophique Vgs2 en m/s et en km/h, à cet endroit en précisant les
isobares utilisées et leurs interdistances
Notes : Pour la mesure des distances, on utilisera l’échelle données sur la carte. Pour la
masse volumique de l’air ρ, on prendra 1.2 kg.m-3.
7) donner vous une échelle et tracer ces vents sur la carte.
8) Compte tenu des forces de friction, le vent réel en surface Vrs est plus faible que le vent
géostrophique et à une orientation différente. Rappeler les relations entre le vent réel et le vent
dans la couche d’Ekman.
9) On peut montrer que Ku(z).u*=f.vg.(z-z0).k.z.
Calculer Ku(z) pour une altitude z = 10m et z0 = 10-4, et u*= vg/30
10) calculer et tracer la vitesse du vent à z=10m
Cohard 06 1/3
Contrôle continu Milieu Naturel

Université Joseph Fourier
Cohard 06 2/3

Université Joseph Fourier
Cohard 06 3/3