Son et mode propre de vibration

Spé Page 1
Son et mode propre de vibration
I Rappel sur le son
I.a Le son est une onde mécanique
Le son ne peux pas se propager dans le vide, c’est donc une onde mécanique.
Les tranche d’air oscillent autour d’une position d’équilibre, on s’intéresse donc à la vitesse v
des tranches d’air.
La compression et la détente des tranches d’air impliquent une légère variation de la pression,
c’est la pression acoustique.
I.b Amplitude et fréquence de l’onde
Animation
• Plus l’amplitude est grande plus le son est fort. Plus la fréquence est grande plus le son
est aigu.
• Domaine audible : 20 Hz à 20 000 Hz
I.c Interférences
II Production d’un son par un instrument de musique
II.a Système mécanique vibrant
Dans un instrument acoustique, un système mécanique vibrant est à l’origine de la production
du son.
• Corde fixée entre deux points fixes (piano, violon, guitare…)
• Une anche (clarinette, saxophone, hautbois…)
• Instrument à biseau ( orgue, pipeau…)
II.b Système assurant le couplage avec l’air
Le système vibrant ne peut pas mettre l’air en vibration, il faut donc un système qui transmette
les vibrations à l’air : c’est le rôle de la caisse de résonnance.
Aquison : 20 000hz et 4000 points
III Vibrations d’une corde entre deux points fixes
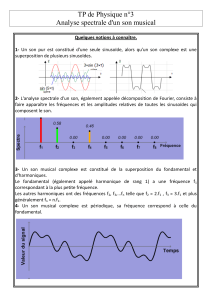
III.a Modes propres de vibration
Animation de 3 modes propres
Représentation de la corde à un instant t

Spé Page 2
DO 1
F
1
= 65,4 Hz
DO2
F
2
= 2 × 65,4 Hz= 131
Hz
Sol 2
F
3
= 3 × 65,4 Hz= 196
Hz
Do 3
F
4
= 4 × 65,4 Hz= 262
Hz
Mi 3
F
5
= 5 × 65,4 Hz= 327
Hz
Sol 3
F
6
= 6 × 65,4 Hz= 392
Hz
Si
b
3
F
7
= 7 × 65,4 Hz= 458
Hz
III.b Mode fondamental et modes harmoniques
• Le mode propre dont la fréquence est la plus basse (ici le do 1) est appelé mode
fondamental : sa fréquence est noté f
1
• Les autres modes propres sont appelés mode harmoniques. Ils sont caractérisés par un
nombre entier n. La fréquence f
n
de l’harmonique n est égale à n fois le fréquence
fondamentale :
ࢌ
࢔
= ࢔. ࢌ
૚
• On constate que les modes propres sont quantifiés
L’accord do, sol, mi est harmonieux car une corde qui produit la note Do contient les
harmoniques qui corresponde au note sol et mi. Autrement dit les notes sol et mi renforcent
les harmoniques du Do.

Spé Page 3
III.c Nœud et ventre de vibration
Représentation de la corde à un instant t
III.d Son émis par une corde pincée ou frappée
Lorsqu’une corde de guitare oscille librement, elle produit un son composé de sons
sinusoïdaux dont les fréquences sont celles des modes propres de la corde.
La note ainsi jouée est celle du mode fondamentale.
Voir Doc 11 et 12 P 53
IV Vibration d’une colonne d’air
IV.a Modes propres pour une colonne d’air
Comme pour la corde de la guitare, ces fréquences sont les fréquences des modes propres de
vibration de la colonne d’air : elles sont quantifiées. Si le mode fondamental a pour fréquence
f
1
, les modes harmoniques ont pour fréquence f
n
= nf
1
où n est un entier.
IV.a.1 Tuyau ouvert
Ventre de vibration Nœud de vibration

Spé Page 4
On constate que ܮ =
ఒ
ଶ
d’où ݂
ଵ
=
஼
ఒ
soit ݂
ଵ
=
஼
ଶ௅
si on n’est plus dans l’air la longueur d’onde ne
varie pas mais le fréquence de résonnance sera modifiée à cause de la variation de la vitesse
du son. Par exemple dans l’hélium le son est plus rapide donc les fréquences de résonnances
sont plus grand et les sons plus aigues
IV.a.2 Tuyau fermé
IV.b Influence de la longueur de la colonne d’air
La fréquence f
1
du mode fondamentale dépend de la longueur L du tube. Plus le tube est court,
plus la valeur de la fréquence du mode fondamental est élevée. Les sont aigus seront favorisés
par des tubes courts et les sont graves par des tubes longs.