Chap 04

MODELE ONDULATOIRE DE LA LUMIERE
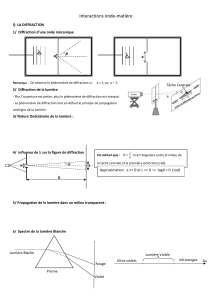
1. LA DIFFRACTION.
1.1. QUELQUES OBSERVATIONS.
Observations.
La figure de diffraction pour une ouverture circulaire est formée d’une tache circulaire
très éclairée (appelée tache de diffraction) entourée d’anneaux alternativement noirs et
éclairés (l’intensité des anneaux éclairés diminuant rapidement quand on s’éloigne du
centre).
La figure de diffraction pour une fente fine est constituée d’une tache centrale brillante
étalée dans une direction perpendiculaire à la fente et, dans la même direction, de taches
brillantes, plus petites et moins lumineuses.
La figure de diffraction pour un fil est semblable à celle du faisceau laser par une fente
Interprétations.
L’ouverture circulaire a diffracté la lumière. La tache de diffraction présente l’éclairement
le plus grand et elle est la seule à prendre en compte.
La fente a diffacté la lumière dans une direction perpendiculaire à cette fente.
Le fil a diffracté la lumière dans une direction perpendiculaire au fil.
Remarques.
Le rayon r de la tache de diffraction est d’autant plus grand que le diamètre a de l’ouver-
ture circulaire est plus petit
Si l’on diminue la largeur de la fente, les taches deviennent plus alrges, en particulier la
tache centrale.
Conclusions.
Comme dans le chapitre précédent, les ouvertures et les obstacles de petites dimensions
diffractent la lumière. Dans le cas des ondes lumineuses, le critère est moins restrictif: le
phénomène est encore bien apparent avec des ouvertures ou des obstacles de dimen-
sions jusqu’à 100 fois plus grandes que la longueur d’onde.
Les phénomènes de diffraction sont d’autant plus marqués que les ouvertures ou les
obstacles diffractant sont plus petits.
Dispositifs.
On dirige le faisceau laser sur
une ouverture circulaire une fente dont la largeur est de quelques
dixièmes de millimètres
On observe sur un écran placé à environ 1 mètre.
un fil très fin, perpendiculairement à ce fil.
La lumière est donc une onde parmi toutes les ondes rencontrées. On peut donc également aborder les notions vues dans le chapitre
précédemment de diffraction et de dispersion.

1.2. ECART ANGULAIRE DE DIFFRACTION POUR UNE LUMIERE MONOCHROMATIQUE.
L’importance du phénomène de diffraction est mesurée par l’écart angulaire de diffraction, angle entre la direction de propagation de
l’onde en l’absence de diffraction, et la direction définie par le milieu de la première extinction.
Cet écart angulaire de diffraction, souvent noté , dépend de la longueur d’onde et de la taille de l’élément diffractant.
En effet, théorie et expérience, montrent que lorsqu’un faisceau parallèle de lumière de longueur
d’onde  traverse une fente de largeur a, l’écart angulaire  entre le centre de la tache centrale et
la première extinction est donné par: 
 =
a
Par ailleurs l’écart angulaire peut-être déterminé par la relation:
d/2 d
tan  =  = =
D 2D
D
d
1.3. CAS PLUS GENERAL D’UNE LUMIERE BLANCHE.
La lumière blanche est une lumière polychromatique composée de toutes les lumières colorées visibles.
Dans le cas de la diffraction de la lumière blanche par une fente, la figure de diffraction présente
également une tache centrale mais bmanche et des taches latérales irrisées.
En simplifiant, on peut restreindre la lumière blanche à la superposition de lumières rouge, verte
et bleue.
Ces différentes radiations se superposent dans des proportions proches dans la tache centrale,
ainsi elle est blanche.
Mais ce n’est pas forcèment le cas de part et d’autre de la tâche centrale, ce qui explique les irrisations.
2. DISPERSION
2.1. MILIEU DISPERSIF
Dans le cas d’une onde lumineuse sinusoïdale (appelée lumière monochromati-
que), la couleur est associée à sa longueur d’onde dans le vide que l’on notera
0. c
Comme 0 = , la couleur ne dépend que de la fréquence f de l’onde.
f
Celle-ci est imposée par la source et ne dépend pas des milieux traversés
Par contre, la célérité v de la lumière dans un milieu quelconque dépend du
c
milieu traversé n = (l’indice de réfraction cette dépendance).
v
Il en est donc de même pour la longueur d’onde 
n
Juste avant les vendanges, les
experts vérifient que le raisin atteint
bien le degré d’alcool potentiel
requis, à l’aide d’un réfractomètre.
Les milieux transparents étant des milieux dispersifs pour la lumière, d’où la formation des spectres de lumière avec un prisme.

2.2. LA SECONDE LOI DE DESCARTES
Lorsqu’un rayon lumineux est réfracté à travers le plan séparant l’air d’un autre milieu transparent, les angles
i1 et i2 qu’il forme avec la normale au plan, dans l’air et dans l’autre milieu, vérifient la relation
n1 x sin i1 = n2 x sin i2,
où n est une constante caractéristique du milieu (n > 1) appelée son
indice de réfraction par rapport à l’air.
Définition.
L’indice de réfraction n’étant rien d’autre que le rapport de la vitesse de la
lumière dans le premier milieu à la vitesse de la lumière dans le deuxième
milieu. En général un des deux milieux est l’air (ou le vide) de sorte que
l’indice de réfraction a pour formule:
vitesse de la lumière dans l’air ou dans le vide c
n = =
vitesse de la lumière dans le deuxième milieu v
L’indice de réfraction est bien une grandeur sans unité.
René Descartes
(1596 - 1650)
Né à La Haye (appelée
aujourd’hui Descartes),
en Touraine.
Il fait ses études chez
les jésuites à la Flèche
..............
milieu
eau
éthanol
altuglas
verre
diamant
n
1,33
1,36
1,50
1,50
2,42
1°) Indiquer, dans chaque cas, sur le schéma: - en vert l’angle d’incidence i et sa valeur;
- en bleu l’angle de réfraction r du rayon lumineux et sa valeur.
2°) Pour chaque schéma, déterminer la valeur inconnue.
3°) Déterminer la célérité de l’onde dans le second milieu traversé.
milieu 1
n1 = 1,00
milieu 2
61,9°
b.
n1 = 1,00
n2 = 1,60
n2 = 1,45
milieu 2
65°
2.3. APPLICATIONS.