Cours 5.1 : La raison et le réel, la vérité, la démonstration, le vivant +

1/4
Cours 5.1 : La raison et le réel, la vérité, la démonstration, le vivant
Séquence 5 – Épistémologie et métaphysique
PLAN
Introduction
(a) Problématique
I – La démonstration en mathématiques
A. La démonstration comme modèle de certitude
B. Les limites de la démonstration
II - L'expérience dans les sciences de la nature
A.. L'empirisme : l'expérience comme source de la connaissance
B. Les critiques de l'empirisme
III – Une connaissance scientifique du vivant est-elle possible ?
A. Le problème de la connaissance de la vie
B. La biologie face à la spécificité du vivant
Introduction
(a) Problématique
Vérité et
opinion Tandis que l'opinion est la simple affirmation d'une idée, la vérité est la correspondance entre une affirmation et la réalité. L'opinion est subjective, relative aux croyances particulières de l'individu, tandis que la vérité est objective et
universelle. Mais comment peut-on être sûr d'être parvenu à une vérité ?
Formulation
de la
problématique
Selon la discipline et l'objet étudié, le moyen utilisé pour parvenir à la vérité semble différent. En mathématiques, on
fait des démonstrations ; dans les sciences de la nature (la physique, la chimie, la biologie), on fait des expériences ;
dans les sciences humaines (la psychologie, la sociologie, l'histoire, …), on vise avant tout une compréhension, une
interprétation des phénomènes humains. La démonstration semble être un modèle de certitude et l'expérience
scientifique un modèle de rigueur, tandis que les sciences humaines sont parfois considérées comme des “sciences
molles” (par opposition aux “sciences dures” ou “sciences exactes”). Cette représentation correspond-elle à la
réalité ? La démonstration mathématique permet-elle vraiment de parvenir à des vérités absolues et incontestables ?
L'expérience dans les sciences de la nature est-elle vraiment une source de connaissance fiable ? Faut-il vraiment
refuser aux sciences humaines le statut de science ?
I – La démonstration en mathématiques
A. La démonstration comme modèle de certitude
Sens large et
sens strict Au sens large, la démonstration se rapporte à tout type de preuve. Au sens strict, la démonstration se rapporte à la démonstration telle qu'elle est pratiquée dans les mathématiques, et c'est ce sens ici qui nous intéresse.
Deux types de
raisonnement :
la déduction et
l'induction
Une démonstration est d'abord une forme de raisonnement. Qu'est-ce qu'un raisonnement ? C'est une inférence qui
tire une conclusion à partir de prémisses (les prémisses sont les points de départ du raisonnement). Il y a deux
grandes formes de raisonnement, selon le lien établi entre les prémisses et la conclusion.
– Dans une induction, si les prémisses sont vraies, alors la conclusion est probablement vraie. L'induction repose sur
une généralisation à partir d'un ensemble d'observations sur le monde. Exemple : “Nous sommes en été. Il a fait beau
ces derniers jours. Il n'y a eu aucun nuage aujourd'hui. Donc : Il fera beau demain.”
– Dans une déduction, si les prémisses sont vraies, alors la conclusion est nécessairement vraie. La déduction repose
sur un lien purement formel entre les idées. Exemple : “Tout nombre divisible par deux est un nombre pair. 4 est un
nombre divisible par deux. Donc : 4 est un nombre pair.”
La
démonstration
n'est pas une
simple
déduction
logique
Une démonstration se fonde sur un raisonnement déductif, purement logique, mais i l ne suffit pas de faire une
déduction pour faire une démonstration. On peut en effet raisonner de manière logique à partir d'affirmations en
elles-mêmes absurdes, qui conduisent, par déduction logique, à une affirmation absurde, que l'on n'aura pas pour
autant démontré. Exemple : “Tous les animaux sont des chaises. Toutes les chaises sont des nombres premiers.
Donc, tous les animaux sont des nombres premiers” (ce raisonnement est une déduction logique, mais on ne peut
pas dire qu'on a démontré que tous les animaux sont des nombres premiers). Pour qu'il y ait une démonstration, il
faut déduire logiquement une conclusion à partir de prémisses reconnues comme vraies.
La
démonstration
à partir
d'axiomes
Quelles sont les prémisses à partir desquelles on peut pratiquer une démonstration en mathématiques ? On peut
utiliser des théorèmes pour faire une démonstration, mais on peut aussi chercher à démontrer les théorèmes que
nous utilisons. Si on poursuit cette démarche, on est alors conduit à remonter vers des principes premiers, vers les
premiers fondements d'une théorie, (ce sont les axiomes de cette théorie). Dans l'histoire des mathématiques, on
observe une telle démarche d'axiomatisation dès l'Antiquité dans les Éléments d'Euclide : « La géométrie classique,
sous la forme que lui a donnée Euclide dans ses Éléments, a longtemps passé pour un modèle insurpassable, et
même difficilement égalable, de théorie déductive. Les termes propres à la théorie n'y sont jamais introduits sans
être définis; les propositions n'y sont jamais avancées sans être démontrées, à l'exception d'un petit nombre d'entre
elles qui sont énoncées d'abord à titre de principes: la démonstration ne peut en effet remonter à l'infini et doit bien
reposer sur quelques propositions premières, mais on a pris soin de les choisir telles qu'aucun doute ne subsiste à
leur égard dans un esprit sain. Bien que tout ce qu'on affirme soit empiriquement vrai, l'expérience n'est pas
invoquée comme justification: le géomètre ne procède que par voie démonstrative, il ne fonde ses preuves que sur ce
qui a été antérieurement établi, en se conformant aux seules lois de la logique. Chaque théorème se trouve ainsi
relié, par un rapport nécessaire, aux propositions dont il se déduit comme conséquence, de sorte que, de proche en
proche, se constitue un réseau serré où, directement ou indirectement, toutes les propositions communiquent entre
elles. L'ensemble forme un système dont on ne pourrait distraire ou modifier une partie sans compromettre le tout.
Ainsi, “les Grecs ont raisonné avec toute la justesse possible dans les mathématiques, et ils ont laissé au genre
humain des modèles de l'art de démontrer” (Leibniz, Nouveaux Essais, IV, II, 13). Avec eux, la géométrie a cessé
d'être un recueil de recettes pratiques ou, au mieux, d'énoncés empiriques, pour devenir une science rationnelle. »
(Blanché, L'axiomatique chap.I, §1)

2/4
La
démonstration
comme
modèle
« [I]l est inscrit dans l'essence des mathématiques que partout où l'on peut donner une preuve, elle est
préférable à une confirmation inductive. Euclide prouve ce qu'on lui aurait bien volontiers accordé. […] C'est que
la preuve n'a pas pour seule fin de libérer une proposition du doute ; elle permet en outre de pénétrer la
dépendance relative des vérités. Une fois persuadé qu'un bloc de rocher est inébranlable parce qu'on a essayé
sans succès de le faire bouger, on peut se demander ce qui le soutient si solidement. Plus on poursuivra la
recherche, moins nombreuses seront les vérités fondamentales auxquelles on pourra tout ramener, et cette
simplification est déjà en elle-même un but digne d'efforts. » (Frege, Les Fondements de l'arithmétique).
B. Les limites de la démonstration
Démonstration
et intuition La démonstration a certes une place essentielle dans les mathématiques, mais il ne faut pas réduire la pratique des mathématiques à la démonstration. La recherche mathématique repose aussi sur l'intuition de connexions,
de liens, d'analogies entre différentes idées mathématiques. Avant de démontrer, il faut avoir une idée de ce
qu'on veut démontrer, et c'est l'intuition qui permet alors d'ouvrir une voie de recherche. Deux citations
éclairantes sur ce point : « C’est par la logique que nous prouvons. C’est par l’intuition que nous inventons »
(Poincaré) ; « La déduction est à l’aveugle ce que l’intuition est au paralytique, l’une avance mais ne se voit pas,
l’autre voit mais n’avance pas » (René Thom)
Le statut des
axiomes On ne voit pas comment on pourrait démontrer les axiomes eux-mêmes, étant donné que les axiomes sont les principes les plus élémentaires d'une théorie. Qu'est-ce qui permet alors d'affirmer la vérité des axiomes si on
ne peut pas les démontrer ?
– Faut-il considérer que les axiomes sont des vérités évidentes par elles-mêmes ? C'est notamment la position
de Pascal : « Nous connaissons la vérité non seulement par la raison mais encore par le cœur. C'est de cette
dernière sorte que nous connaissons les premiers principes et c'est en vain que le raisonnement, qui n'y a point
de part essaie de les combattre. Les pyrrhoniens, qui n'ont que cela pour objet, y travaillent inutilement. Nous
savons que nous ne rêvons point. Quelque impuissance où nous soyons de le prouver par raison, cette
impuissance ne conclut autre chose que la faiblesse de notre raison, mais non pas l'incertitude de toutes nos
connaissances, comme ils le prétendent. Car les connaissances des premiers principes : espace, temps,
mouvement, nombres, sont aussi fermes qu'aucune de celles que nos raisonnements nous donnent et c'est sur
ces connaissances du cœur et de l'instinct qu'il faut que la raison s'appuie et qu'elle y fonde tout son discours.
Le cœur sent qu'il y a trois dimensions dans l'espace et que les nombres sont infinis et la raison démontre
ensuite qu'il n'y a point deux nombres carrés dont l'un soit double de l'autre. Les principes se sentent, les
propositions se concluent et le tout avec certitude quoique par différentes voies et il est aussi inutile et aussi
ridicule que la raison demande au cœur des preuves de ses premiers principes pour vouloir y consentir, qu'il
serait ridicule que le cœur demandât à la raison un sentiment de toutes les propositions qu'elle démontre pour
vouloir les recevoir. » (Pensées L100)
– Mais l'histoire des mathématiques montre que des principes qui semblaient évidents en eux-mêmes se sont en
fait révélés partiellement faux. Par exemple l'idée que “le tout est plus grand que la partie” semble évidente,
mais en fait dans le cas d'une partie infinie d'un ensemble infini, cela n'est plus vrai : notamment, l'ensemble
des nombres entiers (le tout) n'est pas plus grand que l'ensemble des nombres pairs (la partie). En géométrie,
l'axiome des parallèles (“par un point extérieur à une droite passe une et une seule parallèle) semble évident – il
existe des géométries dites non-euclidiennes par lesquels, par un point extérieur à une droite, on a une infinité
de parallèles, ou bien aucune).
– Plusieurs systèmes axiomatiques semblent donc possibles, avec des théorèmes différents. Une vérité
démontrée ne l'est qu'à l'intérieur d'un système théorique particulier. Le choix d'un cadre théorique par rapport
à un autre, n'est pas une question de vérité, mais d'utilité, de pertinence. C'est notamment la position de
Poincaré : « Dès lors, que doit-on penser de cette question : La géométrie euclidienne est-elle vraie ? Elle n'a
aucun sens. Autant demander si le système métrique est vrai et les anciennes mesures fausses ; si les
coordonnées cartésiennes sont vraies et les coordonnées polaires fausses. Une géométrie ne peut pas être plus
vraie qu'une autre ; elle peut seulement être plus commode. » (La Science et l'Hypothèse, ch. III)
II - L'expérience dans les sciences de la nature
A.. L'empirisme : l'expérience comme source de la connaissance
L'expérience
comme point de
départ pour
construire une
théorie
(l'empirisme de
la découverte)
L'empirisme consiste tout à d'abord à privilégier l'observation des faits, du réel concret plutôt que l'élaboration
de constructions intellectuelles abstraites (l'empirisme s'oppose en ce sens à l'idéalisme ; cf. la représentation
de Platon et d'Aristote dans la fresque de Raphaël, L'École d'Athènes). L'expérience est en effet considérée
comme le point de départ de la connaissance : pour l'empirisme, il n'y a pas de connaissance a priori (avant
d'avoir fait une expérience). La connaissance est a posteriori : elle dérive de l'expérience. Sans l'expérience,
l'esprit serait une “table rase” (Locke) et il serait impossible d'avoir une connaissance a priori du monde. Hume
affirme en ce sens que : « Si nous raisonnons a priori, n'importe quoi peut paraître capable de produire
n'importe quoi. […]. C'est seulement l'expérience qui nous apprend la nature et les limites de la cause et de
l'effet et nous rend capables d'inférer l'existence d'un objet de celle d'un autre. » ( Enquête sur l'entendement
humain).
L'expérience
comme preuve
de la vérité
d'une théorie
(l'empirisme de
la justification)
L'expérience d'un grand nombre d'observations particulières qui confirment une théorie semble pouvoir jouer
le rôle de preuve de la vérité de cette théorie. On a ici une forme de raisonnement par induction, par
généralisation à partir des cas particuliers qui confirment la théorie : si la théorie a été à chaque fois
confirmée, c'est qu'elle est vraie, ou du moins, probablement vraie, et l'on pourrait affiner ce jugement en
formulant un degré de probabilité de vérité de la théorie, qui approcherait de la certitude au fur et à mesure
qu'on accumule des données qui vont dans le sens de la théorie.

3/4
B. Les critiques de l'empirisme
L’expérience
est-elle
vraiment le
point de
départ des
théories
scientifiques ?
– L'histoire des sciences semble montrer que le plus souvent, c'est la théorie qui précède l'expérience. Par exemple, la
planète Neptune a d'abord été une hypothèse théorique avant d'être observée réellement. Urbain Le Verrier cherchait à
comprendre le décalage entre la trajectoire théorique (calculée grâce aux lois de Newton) et la trajectoire réelle d'Uranus
: son hypothèse est qu'il existe une planète qui, du fait de sa masse et de sa position, attire Uranus dans une trajectoire
qui n'est pas celle initialement calculée (sans prendre en compte cette planète). Urbain Le Verrier calcule la masse et la
position théoriques de cette planète ; il envoie ses résultats à Galle, en lui indiquant où il devrait pouvoir observer dans
le ciel cette planète ; Galle observe bel et bien cette “nouvelle” planète que l'on appelera Neptune.
– Quelles sont les raisons pour lesquelles la théorie précède l'expérience ? (i) L’expérience, dans sa finalité, vise à tester
une théorie. C’est la théorie qui définit ce qu'on cherche à observer : l’observation dans une expérimentation n’est pas
passive, elle est une recherche active d’informations, guidée par la théorie. (ii) L'expérience, du point de vue des moyens
employés, repose sur des instruments scientifiques de mesure et d'observation. Or la fabrication et l’utilisation de ces
instruments scientifiques dépendent de la maîtrise de théories scientifiques (la contruction d'un microscope à effet tunel
repose sur la connaissance d'un phénomène (l'effet tunnel) qui relève de la physique quantique ; l'utilisation d'imageries
médicales par radiographie suppose des connaissances médicales). Bachelard écrit en ce sens que « les instruments ne
sont que des théories matérialisées. Il en sort des phénomènes qui portent de toutes parts la marque théorique ». De
manière plus générale, c'est la théorie qui permet de définir un protocole expérimental qui doit permettre d'obtenir des
conditions optimales d'observation.
L'expérience
peut-elle
vraiment
jouer le rôle
d'une
preuve ?
– L’expérience permet-elle vraiment de prouver la vérité d’une théorie ? Ne faut-il pas critiquer l'induction par laquelle
on passe d'une série d'observations particulières à l'affirmation d'une vérité générale ? Même si une théorie se vérifie de
nombreuses fois dans des expériences diverses, il est possible qu'il y ait une exception que l'on n'ait pas encore pris en
compte. Dans l'histoire des sciences, on peut prendre l'exemple de la théorie de Newton : elle s'appliquait très bien à de
nombreux phénomènes très différents : l'explication de la trajectoire d'un projectile, des marées, du mouvement des
planètes…, de sorte qu'on a cru qu'elle énonçait une vérité définitive sur le monde. Pourtant Einstein a montré que les
lois de Newton ne sont que des approximations, qui ne fonctionnent plus lorsqu'on a des vitesses qui s'approchent de
celle de la lumière.
– Si l'expérience ne peut constituer une preuve définitive de la vérité d'une théorie, elle semble permettre de pouvoir
prouver la fausseté d'une théorie. En effet, si à partir d'une théorie, on déduit une conséquence que l'on devrait pouvoir
observer, et si l'expérience montre que l'on n'obtient pas cette conséquence, cela signifie que la théorie n'est pas bonne :
on a alors déduit logiquement la fausseté de la théorie à partir de l'expérience. Et il s'agit bien d'une déduction logique,
et non d'une induction, ce qui autorise dans ce cas-là à dire que l'expérience peut prouver la fausseté d'une théorie.
– Toute la démarche scientifique repose sur ce principe selon Popper : une théorie scientifique est une théorie ouverte à
la critique, qui ne s'immunise pas contre la critique, et qui cherche donc à faire des expériences pour tester les théories,
pour les éprouver. Une théorie n'est scientifique que si elle est réfutable.
– Mais l’expérience peut-elle vraiment jouer le rôle de critère de fausseté ? Peut-il y avoir vraiment pour une théorie ce
que l'on appelle une “expérience cruciale” ? Si l’expérience n’est pas en accord avec la théorie, il y a trois possibilités : (i)
la théorie est fausse, (ii) l’expérience est faussée (cas des neutrinos), (iii) on peut sauver la théorie en ajoutant,
supprimant ou modifiant des hypothèses secondaires (cas de la découverte de Neptune : l'observation de la trajectoire
d'Uranus ne correspond pas à ce que l'on trouve grâce à un calcul à partir des lois de Newton, mais cela ne signifie pas
pour Urbain Le Verrier que la théorie de Newton est fausse : il ajoute simplement une hypothèse, selon laquelle il doit
exister une “nouvelle” planète (Neptune) qui explique le problème qui se posait).
III – Une connaissance scientifique du vivant est-elle possible ?
A. Le problème de la connaissance de la vie
L'animisme Cette perspective consiste à affirmer que la vie se définit par la possession d'une âme qui anime un individu. Aristote
distingue 3 types d'âmes : l'âme végétative qui se rapport aux phénomènes de nutrition et de croissance que l'on
observe déjà chez les végétaux ; l'âme motrice et sensitive qui se rapporte à la capacité des animaux à se déplacer
grâce aux informations venues des sens, l'âme intellective (l'âme des hommes), qui se rapporte à la pensée rationnelle
propre aux êtres humains. De manière générale, l'animisme vise à décrire la spécificité du vivant, mais il peine à
l'expliquer scientifiquement.
Le
mécanisme Cette perspective consiste à réduire le vivant à de la matière, et à expliquer le caractère animé du vivant à la manière d'un automate, d'une machine. On retrouve cette idée dans la thèse des animaux machines de Descartes, ou dans
L'Homme Machine de La Mettrie. [Exemples : le canard de Vaucanson, le robot-blatte, BigDog (on emploie parfois
aujourd'hui le terme d'animats)]. De manière générale le mécanisme vise à expliquer scientifiquement le vivant, mais il
en perd la spécificité.
Le problème Est-il possible d'expliquer scientifiquement le vivant sans perdre les spécificités qui constituent le vivant ?
B. La biologie face à la spécificité du vivant
La
spécificité
du vivant
– La complexité du vivant : le vivant se présente sous la forme d'une diversité importante des espèces et des individus
au sein d’une espèce. Y a-t-il vraiment par conséquent des lois générales en biologie et en médecine comme il peut y
avoir en physique ou en chimie ?
– La faculté d’auto-organisation du vivant : le vivant est capable d'auto-réparation (exemple de la cicatrisation), d'auto-
régulation (exemple de la sueur), d'un métabolisme. Le vivant semble donc fonctionner comme un tout qui cherche à se
conserver dans l'existence. En ce sens Bichat affirme que “la vie, c’est l’ensemble des fonctions qui résistent à la mort”.
– L’auto-reproduction du vivant : comment un être vivant peut-il produire une réplique de lui-même ? Comment peut-
on penser l’origine de la vie étant donné qu’un être vivant provient d’un autre être vivant ?
– Les questions de bioéthique : la question du rapport à la nature, et la question de la souffrance animale.
La biologie
moderne
face à la
spécificité
du vivant
– Face à la complexité du vivant : la théorie de l’évolution permet d'expliquer la diversité du vivant (exemple de la
phalène du bouleau).
– Face à l’auto-organisation du vivant : la physiologie expérimentale permet l’analyse des fonctions du vivant (exemple
de la fonction glycogénique du foie analysée par Claude Bernard).
– Face à l’auto-reproduction du vivant : la génétique permet de mieux comprendre l’hérédité, mais l’origine générale de
la vie reste globalement un mystère du point de vue scientifique.
– Face aux questions de bioéthique : la biologie moderne et la médecine sont soumises aux lois (certaines pratiques,
certaines expérimentations ne sont pas acceptées) et elles ne sont pas hermétiques au questionnement éthique issu de
la société civile et des comités d'éthique auxquels elle fait appel.

4/4
Cours 5.2 : La religion
Séquence 5 – Épistémologie et métaphysique
PLAN
Introduction
(a) Problématique
I – Peut-on expliquer le fait religieux ?
A. Les sciences humaines et la religion
B. Les limites de cette approche
II - La croyance en un dieu est-elle rationnelle ?
A.. Peut-on prouver que Dieu existe ?
B. Peut-on prouver que Dieu n'existe pas ?
Introduction
(a) Problématique
Formulation
de la
problématique
La spécificité des croyances religieuses nous invite à les questionner du point de leur origine de fait (comment peut-on expliquer
leur force, leur impact aussi important sur les individus et dans l'histoire de l'humanité ?) et du point de vue de leur fondement en
droit (les croyances religieuses sont-elles rationnelles ? Doit-on les considérer comme irrationnelles ?).
I – Peut-on expliquer le fait religieux ?
A. Les sciences humaines et la religion
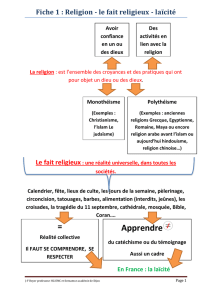
Définition
de la notion
de religion
Il y a trois caractéristiques d'une religion : une religion, c'est (i) un univers de croyances et de pratiques ; c'est aussi (ii) une
communauté organisée (la religion relie horizontalement les gens entre eux) ; c'est enfin, (iii) une relation au sacré (la religion est un
lien vertical avec un sacré qui se distingue du monde profane).
Religion et
psychologie – Le modèle de Freud : la religion est une illusion, une croyance qui dérive de trois désirs fondamentaux des êtres humains : un besoin affectif de protection (Dieu est une sorte de projection de la figure du Père), un besoin intellectuel de compréhension du
monde et de soi-même (la religion prétend répondre aux grandes questions métaphysiques : quelle est l'origine du monde ? Quel est
le sens de la vie ?), un besoin moral de justice (cf. le “jugement dernier”, l'idée d'un paradis, d'un enfer, l'idée d'un Dieu qui voit tous
les actes et intentions des hommes, …).
Religion et
sociologie – Le modèle de Durkheim : la religion est avant tout une forme de lien social. « Il y a donc dans la religion quelque chose d’éternel qui est destiné à survivre à tous les symbolismes particuliers dans lesquels la pensée religieuse s’est successivement enveloppée. Il
ne peut pas y avoir de société qui ne sente le besoin d’entretenir et de raffermir, à intervalles réguliers, les sentiments collectifs et
les idées collectives qui font son unité et sa personnalité. Or, cette réfection morale ne peut être obtenue qu’au moyen de réunions,
d’assemblées, de congrégations où les individus, étroitement rapprochés les uns des autres, réaffirment en commun leurs communs
sentiments ; de là, des cérémonies qui, par leur objet, par les résultats qu’elles produisent, par les procédés qui y sont employés, ne
diffèrent pas en nature des cérémonies religieuses. » (Les Formes élémentaires de la vie religieuse)
Religion et
économie – Le modèle de Marx : la religion est “l'opium du peuple”. La religion naît dans un contexte de misère matérielle, d’incapacité à maîtriser les conditions d’existence ; la religion prétend délivrer l’individu de la sensation de souffrance (elle anesthésie, donne de
l’espoir...), mais elle ne délivre pas des causes de la souffrance (elle maintient dans l’inaction, la léthargie ; elle empêche de se
révolter contre l’état-de-fait).
B. Les limites de cette approche
Objection Pourtant, la religion n'est-elle qu'une posture de réaction, un refuge, un repli face à l’angoisse des individus (Freud), face à la
dissolution du lien social (Durkheim), face à la misère économique (Marx) ?
Religion
statique et
religion
dynamique
Bergson oppose deux aspects de la religion. La religion statique correspond à la religion instituée, qui s'est fixée dans des dogmes,
des pratiques, des lieux de culte. La religion dynamique correspond au contraire à un élan spirituel intérieur ( cf. l’expérience
mystique, le phénomène de la foi qui n'est pas le simple fait de croire que Dieu existe, mais le fait de croire en Dieu), et cet élan
spirituel intérieur ne semble pas se réduire aux analyses que proposent les sciences humaines.
II - La croyance en un dieu est-elle rationnelle ?
A.. Peut-on prouver que Dieu existe ?
L'argument
cosmologique Si tout chose a une cause, alors il doit y avoir une cause du monde et ce serait Dieu. Objection : la religion propose une réponse à une question issue de la raison (qui cherche une explication à l’existence du monde), mais la réponse qu’elle propose dépasse le
cadre de la raison.
L'argument
téléologique Le monde présente un degré important de complexité et d’organisation, qui ne pourrait s’expliquer que par la présence d’une cause intelligente (cf. l’exemple de la montre trouvée sur une île déserte (Paley) : on ne suppose pas qu'elle s'est créée toute seule,
par hasard). Objection principale : la théorie de l’évolution offre le modèle d’une explication de phénomènes complexes qui ne
repose pas sur l’appel à une cause intelligente (la sélection naturelle repose sur le hasard et sur des processus non-intentionnels).
B. Peut-on prouver que Dieu n'existe pas ?
L'argument
naturaliste Dans les sciences de la nature, une hypothèse qui affirme l'existence d'une entité n'est justifiée que dans deux cas : soit cette entité est observable directement, soit un raisonnement indirect nous conduit à accepter cette hypothèse, en raison de son pouvoir
explicatif. Mais Dieu n'est pas observable, et l'hypothèse d'un Dieu n'a pas un grand pouvoir explicatif, il n'y aurait donc pas de
bonne raison de croire en Dieu (d'autant plus que la meilleure explication de cette croyance serait plutôt de ne voir en elle qu'une
illusion enracinée dans des désirs humains). Objection : Cet argument n'est pas une preuve de l'inexistence de Dieu, mais prétend
simplement prouver qu'il n'est pas rationnel de croire en Dieu. Cependant, la rationalité d'une croyance doit-elle se définir à partir
de la méthodologie des sciences de la nature ?
L'argument
du mal Si le mal existe, et si Dieu est bienveillant, omniscient et omnipotent, alors il n'est pas possible que Dieu existe (sinon il aurait fait en sorte que le mal n'existe pas). Objection : il y a des théodicées qui cherchent à défendre l’existence de Dieu contre l’argument du mal
(exemples : la théodicée fondée sur l’argument du libre arbitre humain ; la théodicée fondée sur l'incapacité de la raison à
comprendre les raisons de Dieu, étant donné que Dieu, être infini, ne peut être compris par la raison d'un individu, qui n'est qu'une
créature finie, soumise à la finitude).