PYTHON TP 2 matplotlib, numpy,scipy

PYTHON TP 2
matplotlib, numpy,scipy
Vous devez rendre des programmes commentés et expliquer vos choix de
conception : choix des structures de données, enchaînement des fonctions,....
1. Prise en main de matplotlib
Références : numpy : http://docs.scipy.org
http://wiki.scipy.org/Tentative_NumPy_Tutorial
matplotlib :http://matplotlib.org/
Depuis l'interpréteur python afficher la courbe représentative de la fonction :
sur l'intervalle [-4;4] avec 1000 points.
On utilisera les modules numpy et matplotlib.pyplot et notamment : arange ou
linspace, plot, show et savefig.
Utilisez les fonctions mathématiques de numpy de préférence aux fonctions de
même nom de math car elles peuvent prendre directement des vecteurs en
paramètres (array de numpy ou liste de python).
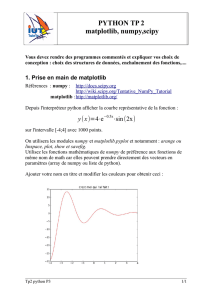
Ajouter votre nom en titre et modifier les couleurs pour obtenir ceci :
Tp2 python P3 1/1
y(x)=4⋅e−0.5x ⋅sin(2x)

PYTHON TP 2
matplotlib, numpy,scipy
Sauver le graphique en png.
Donner la liste des instructions utilisées.
Ajouter sur les mêmes axes la fonction en couleur verte :
Créer un graphique montrant y et z comme ci dessous (dans un programme
python) :
Tp2 python P3 2/1
z(x)=4⋅e−0.3x ⋅sin(3x)

PYTHON TP 2
matplotlib, numpy,scipy
2. "Ploter" des données issues d'un fichier
Le fichier thermistance.csv contient la valeur de la résistance mesurée
en fonction de la température pour deux thermistances.
Le format est le suivant :
#t(°C);Rth1(Ohm);Rth2(Ohm)
-40;57658;101275
-35;42410;76325
....
Écrire une fonction qui lit le fichier csv et retourne une liste pour chaque
colonne de valeurs.
Votre fonction aura la signature suivante :
ReadCSV(filename,cols=1, separator=';', comment='#' )
Ainsi on pourra l'utiliser pour différents formats en changeant les paramètres.
Lorsqu'on lit une valeur, on tentera (try/except) d'abord de la convertir en réel.
Si ce n'est pas possible, la valeur sera laissée en chaîne. Si une valeur est absente
on mettra une chaîne vide dans la liste.
Faire un graphique de la résistance en fonction de la température.
3. Curve Fitting
En première approximation, la résistance d'une thermistance suit la loi :
où T est la température absolue en kelvin :
T(K)=t(° C )+273,15 K
et
RT0
est la résistance à la température absolue
T0
L'objectif est de trouver la "meilleure" valeur pour les paramètres
RT0
et B
en fonction des valeurs mesurées. On cherche la valeur des paramètres qui
minimisent l'erreur entre la courbe réelle et la courbe estimée par la formule.
En général on choisit un critère quadratique (somme des carrés des écarts) à
minimiser. Voir : méthode des moindres carrés (least square).
Les algorithmes peuvent être assez complexes car il faut éviter de s'arrêter sur
des minimums locaux.
Tp2 python P3 3/1
R(T)=RT0 ⋅e(B(1/T−1/T0))

PYTHON TP 2
matplotlib, numpy,scipy
La bibliothèque python scpipy fournit une fonction d'optimisation très puissante
utilisant cette méthode appelée curve_fit
Voir :
docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.curve_fit.html
(et bien comprendre l'exemple)
Les fonctions à optimiser doivent être écrites en python avec les fonctions
mathématiques de numpy car elles doivent pouvoir être utilisées avec des listes
(et des array de numpy). En particulier utilisez np.add pour les additions.
Estimer les paramètres
RT0
et B pour les deux thermistances en fixant
t0
à
25°C.
Faire un graphique montrant les points de mesures, la courbe estimée obtenue
ainsi que l'écart (en Ohm) entre les valeurs mesurées et les valeurs calculées.
Pour améliorer l'approximation on peut utiliser la formule :
R(T)=RT0 ⋅e
(A+B
T+C
T2+D T3)
Estimer les paramètres
RT0
, A,B,C,D pour les deux thermistances.
Faire un graphique montrant les points de mesures, la courbe estimée obtenue
ainsi que l'écart (en Ohm) entre les valeurs mesurées et les valeurs calculées.
4. Estimation de la fréquence à l'aide de la Transformée de
Fourrier Discrète
Le format wav est un format très utilisé pour stocker des fichiers audio. Comme
il s'agit d'un format non compressé (en général), on peut l'utiliser pour stocker
un signal échantillonné quelconque issu d'une expérience.
Le fichier sample.wav contient les valeurs d'un signal échantillonné à 8kHz.
Le module scipy.io contient des fonctions de lecture et d'écriture de fichier wav.
Créer un graphique de ce fichier et montrer que le signal présente
principalement deux fréquences. Estimer ces deux fréquences.
Faire un graphique du signal entre 2.95 et 3,02s dans lequel la plus haute
fréquence apparaît en rouge et la plus basse en vert.
Tp2 python P3 4/1

PYTHON TP 2
matplotlib, numpy,scipy
La Transformée de Fourier Discrète (TFD) est une opération mathématique qui
permet d'obtenir le spectre échantillonné d'un signal échantillonné.
Si on dispose de N valeurs d'un signal aux instants
n⋅Ts
,
n∈[0...N−1]
, la
TFD donne N valeurs (en général complexes) de la transformée de Fourier de
ce signal aux fréquences
k⋅fs/N
avec
k∈[−N/2; N /2−1]
et
fs=1/Ts
Pour un signal réel, les valeurs pour k et -k sont complexes conjuguées (le
spectre est symétrique par rapport à la fréquence 0).
Le spectre en amplitude est obtenu en prenant le module de valeurs de la TFD.
Voir :
http://fr.wikipedia.org : Transformée de Fourier Discrète
http://docs.scipy.org/doc/numpy/reference/routines.fft.html#module-numpy.fft
Pour calculer la TFD, on utilise souvent l’algorithme rapide appelé FFT. Cet
algorithme est implémenté dans le module fft de numpy.
Il faut bien comprendre comment sont classés les coefficients (voir
Implementation details).
On peut utiliser fftfreq pour retrouver les fréquences réelles en fonction de
fe
Tracez le spectre du signal de l'exercice précédent entre 0 et 4kHz pour faire
apparaître les deux fréquences détectées précédemment.
5. Décodage d'un signal DTMF
Le code DTMF est utilisé pour la numérotation en téléphonique analogique ainsi
que pour l'interface utilisateur des serveurs vocaux (messageries, hotline, etc...).
On peut encoder 16 caractères par un signal composé de deux fréquences
choisies parmi deux groupes de quatre. Généralement on encode les touches que
l'on trouve sur les claviers des téléphones : les chiffres de 0 à 9 ainsi que les
caractères A,B,C,D, * et #.
Chaque code est composé d'une fréquence du groupe haut
(1029,1336,1477,1633Hz) et d'une fréquence du groupe bas (697,770,852,941
Hz) selon le tableau ci dessous :
1 209 Hz 1 336 Hz 1 477 Hz 1 633 Hz
697 Hz 123A
770 Hz 456B
852 Hz 789C
941 Hz *0#D
Tp2 python P3 5/1