Transport électronique dans une molécule : une nouvelle diode

L’électronique moléculaire utilise naturellement une
approche « montante » (dite « bottom-up » en
anglais) très féconde, où l’on construit un composant
par assemblage de nano-objets (d’atomes, de molécules,...).
Cette approche s’oppose à l’approche « descendante » (dite
« top-down ») usuelle en micro-électronique, qui procède
par réduction d’échelle successive d’un objet donné (par
exemple, un transistor) et ceci grâce au progrès technolo-
giques des moyens de lithographie. Ainsi, dans l’approche
« montante », en partant d’une molécule, choisie pour ses
propriétés électroniques particulières, on exploite les pro-
priétés d’auto-organisation et d’auto-assemblage de ces
molécules et l’on fabrique des systèmes électroniques. Ces
composants du futur sont donc constitués d’une ou de
quelques molécules réalisant ainsi une fonction de traite-
ment de l’information. Il peut s’agir d’un fil moléculaire,
d’une diode moléculaire, ou encore d’une mémoire molécu-
laire. Des effets quantiques, comme l’effet tunnel résonant,
ont été observés sur des jonctions métal/molécules/métal.
Des prototypes de diodes moléculaires rectificatrices du
courant (le courant passe dans un seul sens) ont aussi été
réalisés. Un circuit logique organique (un réseau de points
mémoires) a été fabriqué. Chaque point mémoire est consti-
tué par l’assemblage d’un petit nombre de molécules orga-
niques entre deux électrodes.
Ces recherches sont accompagnées par de nouvelles
approches théoriques, qui permettent de calculer la structure
électronique de molécules connectées à des électrodes et de
prédire la caractéristique courant-tension de la jonction.
Plusieurs phénomènes physiques sont à considérer : (i) les
interactions aux interfaces molécules/métal ou molécules/
semiconducteur ; (ii) le transport hors-équilibre des élec-
trons et des trous dans le système et les interactions avec les
modes de vibrations de la molécule ; (iii) la modification de
la structure électronique de la molécule sous l’effet de la
tension appliquée entre les électrodes. De nombreux progrès
ont été réalisés récemment pour résoudre ces problèmes
complexes en s’appuyant sur des techniques de calculs ab
initio (partant des premiers principes de la mécanique quan-
tique) ou semi-empiriques (comportant un certain nombre
de paramètres). Mais les difficultés à surmonter restent
nombreuses.
186
Transport électronique
dans une molécule :
une nouvelle diode
En 1974, dans leur proposition théorique, Aviram et Ratner démontrent un effet de redressement du courant
par une molécule organique : le concept de diode moléculaire est né. Ce n’est toutefois que vingt ans plus tard
que les chercheurs ont pu mesurer expérimentalement la conductance d’une molécule unique, grâce au
microscope à effet tunnel, ouvrant ainsi la voie à une nouvelle électronique, « l’électronique moléculaire ».
Depuis, les expériences se multiplient autour des diodes moléculaires, mais aussi des transistors à base de
nanotubes de carbone ou des circuits à mémoires moléculaires. Cet article tente de faire le point sur la
physique du transport d’une diode moléculaire, à partir d’études expérimentales et théoriques récentes.
Article proposé par :
Dominique Vuillaume, [email protected]
Christophe Delerue, [email protected]
Institut d'Electronique, de Microélectronique de Nanoélectronique et de Nanotechnologie, CNRS/Université Lille 1.
Ont participé à ce travail, S. Lenfant, J. Collet (IEMN) pour les expériences, C. Krzeminski, G. Allan (IEMN) pour la théorie, O. Bouloussa
(Institut Curie), F. Tran-Van, C. Chevrot (Univ. Cergy-Pontoise), S. Palacin (CEA-Saclay) pour la synthèse de certaines des molécules, F. Ron-
delez (Institut Curie) pour son expertise et ses conseils sur les greffages chimiques, et R.M. Metzger (Univ. d'Alabama) sur les diodes molé-
culaires de type Avirma et Ratner.
Quanta et photons

187
Quanta et photons
Nous présentons, comme illustration de ces progrès
récents, des résultats expérimentaux et théoriques sur les
propriétés de transport électrique dans des diodes molécu-
laires.
La diode Aviram et Ratner
Dans leur proposition initiale, purement théorique, Avi-
ram et Ratner proposaient qu’une molécule, comportant un
groupement donneur d’électrons et un groupement accep-
teur d’électrons attachés ensemble par un « pont » molécu-
laire, se comporterait de manière équivalente à une jonction
p-n classique de la microélectronique à semiconducteur
(encadré 1).
Actuellement la seule molécule de type « donneur-pont-
accepteur » ayant donnée les résultats expérimentaux les
plus significatifs est la molécule d’héxadecyl- quinolinium
tricyanoquino-dimethanide – C16H33-Q-3CNQ – (figure 1).
Une monocouche de cette molécule prise en sandwich entre
deux électrodes métalliques (Al ou Au) donne bien un effet
redresseur de courant (rapport de redressement d’environ
30) comme l’illustre la figure 1. Le sens de la rectification
(courant plus élevé pour une tension positive sur l’électrode
qui se trouve du côté du donneur – le groupe quinolinium)
correspond à la suggestion de Aviram et Ratner : un transfert
intramoléculaire d’électrons est plus aisé du groupement
accepteur vers le donneur que l’inverse. Toutefois, deux dif-
férences existent entre la molécule C16H33-Q-3CNQ et
l’idée initiale de Aviram et Ratner : i) le pont liant physique-
ment les deux groupes est π-conjugué dans le cas expéri-
mental (une molécule π-conjugué est une molécule avec une
alternance de simple et de double liaisons), tandis qu’il est
formé de liaisons saturées (σ) dans la proposition théorique ;
ii) la molécule expérimentale est substituée à son extrémité
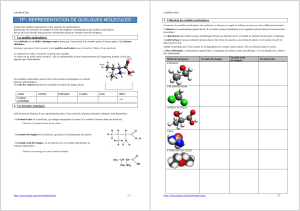
Le modèle de Aviram et Ratner
L’idée de base consiste à utiliser une molécule constituée d’un
groupe donneur d’électron D et d’un groupe accepteur d’élec-
tron A, séparée par un pont ou un liant isolant. Cette molécule
est ensuite prise en sandwich entre deux électrodes. Une petite
barrière tunnel (en rouge) existe entre la molécule et les élec-
trodes de métal. Il peut s’agir d’une très faible couche d’oxyde
(par exemple alumine si on utilise des électrodes en aluminium).
La structure énergétique de cette jonction métal-molécule-métal
montre que les orbitales moléculaires du groupe donneur sont
décalées vers les plus hautes énergies par rapport à celle du
groupe accepteur (figure). L’orbitale LUMO est la première
orbitale moléculaire vide d’électron et l’orbitale HOMO est la
dernière orbitale moléculaire remplie. Par nature, le groupe
donneur ne doit pas avoir une trop grande énergie d’ionisation,
ID, le groupe accepteur ne doit pas avoir une affinité électro-
nique, AA, trop faible. Le modèle d’Aviram et Ratner suppose
que l’on choisit les groupes. donneurs et accepteurs tel que AA
< ID. Sous l’effet d’une faible tension positive sur l’électrode
M1, un électron peut être transféré de l’électrode M2 sur la
LUMO de l’accepteur tandis qu’un autre électron sera transfé-
ré de la HOMO du donneur vers l’électrode M1. Cela conduit à
un état excité de la molécule A––D+. La molécule retourne alors
facilement à l’état stable par un transfert intramoléculaire de la
LUMO de l’accepteur vers la HOMO du donneur.
Il en résulte le passage d’un flux d’électrons de l’électrode M2
vers M1. Pour une tension faiblement négative sur M1, le trans-
fert d’électron est très peu probable, l’électron ayant à franchir
la barrière d’énergie entre la HOMO du donneur et la LUMO
de l’accepteur. Cela conduit donc à un transfert préférentiel
d’électrons de l’électrode M2 vers M1, et donc à un effet de
redressement du courant.
Encadré 1
Figure 1 - Courbe courant-tension typique d'une jonction métal/ C16H33-Q-
3CNQ/métal représenté en encart. L'électrode du côté accepteur est à la
masse et on applique la tension sur l'électrode côté donneur.

« donneur » par une longue chaîne aliphatique (chaîne
hydrocarbonée de ngroupes CH2, soit (CH2)n). Cette chaîne
est nécessaire pour rendre la molécule amphiphile (molé-
cule comportant une partie hydrophile, qui aime bien l’eau
– c’est la partie π– conjuguée – et une partie hydrophobe,
qui n’aime pas l’eau – c’est la chaîne aliphatique (CH2)n).
Cette molécule amphiphile est alors apte à la formation
d’une monocouche par la technique de Langmuir-Blodgett.
Ces deux différences ont des impacts importants sur les pro-
priétés de transport électronique comme nous allons le voir.
Théorie du transport dans les jonctions
moléculaires
Afin de mieux comprendre ces effets, nous avons entre-
pris un calcul du courant dans ces diodes moléculaires.
Compte-tenu de la complexité de ces systèmes, notre
approche consiste à combiner des calculs ab initio (voir
Images de la Physique 2003) et des calculs semi-empiriques
par la méthode des liaisons fortes. Les calculs ab initio sont
utilisés pour optimiser la géométrie des molécules isolées.
L’approche semi-empirique est appliquée à la description
des jonctions et au calcul du courant. Les paramètres de liai-
sons fortes sont obtenus en ajustant la structure électronique
de molécules élémentaires sur celle obtenue par les
méthodes ab initio. Ces paramètres sont ensuite transférés
aux molécules plus complexes comme C16H33-Q-3CNQ.
Nous avons utilisé une méthode auto-cohérente de liaisons
fortes, c’est-à-dire que les équations de Schrödinger et de
Poisson sont couplées et sont résolues simultanément jus-
qu’à convergence pour prendre en compte l’influence de la
tension appliquée sur la molécule. Ceci nous permet de
prendre en compte la répartition complexe du champ élec-
trique dans la jonction moléculaire en fonction de la tension
appliquée. Le courant électrique (la conductance G) est
obtenu en calculant le coefficient de transmission T de la
diode (probabilité de transmettre les électrons d’une élec-
trode à l’autre), et en considérant la diffusion élastique des
électrons à travers la jonction moléculaire. La conductance
et le coefficient de transmission sont reliés par la formule de
Landauer
G=2e2
hT
où eest la charge de l’électron et hla constante de Planck.
Avec un pont à liaisons saturées, le modèle de Aviram et
Ratner suppose que les orbitales moléculaires des groupe-
ments donneur et accepteur restent localisées sur leurs grou-
pements respectifs. En réalité, avec le pont π-conjugué, il
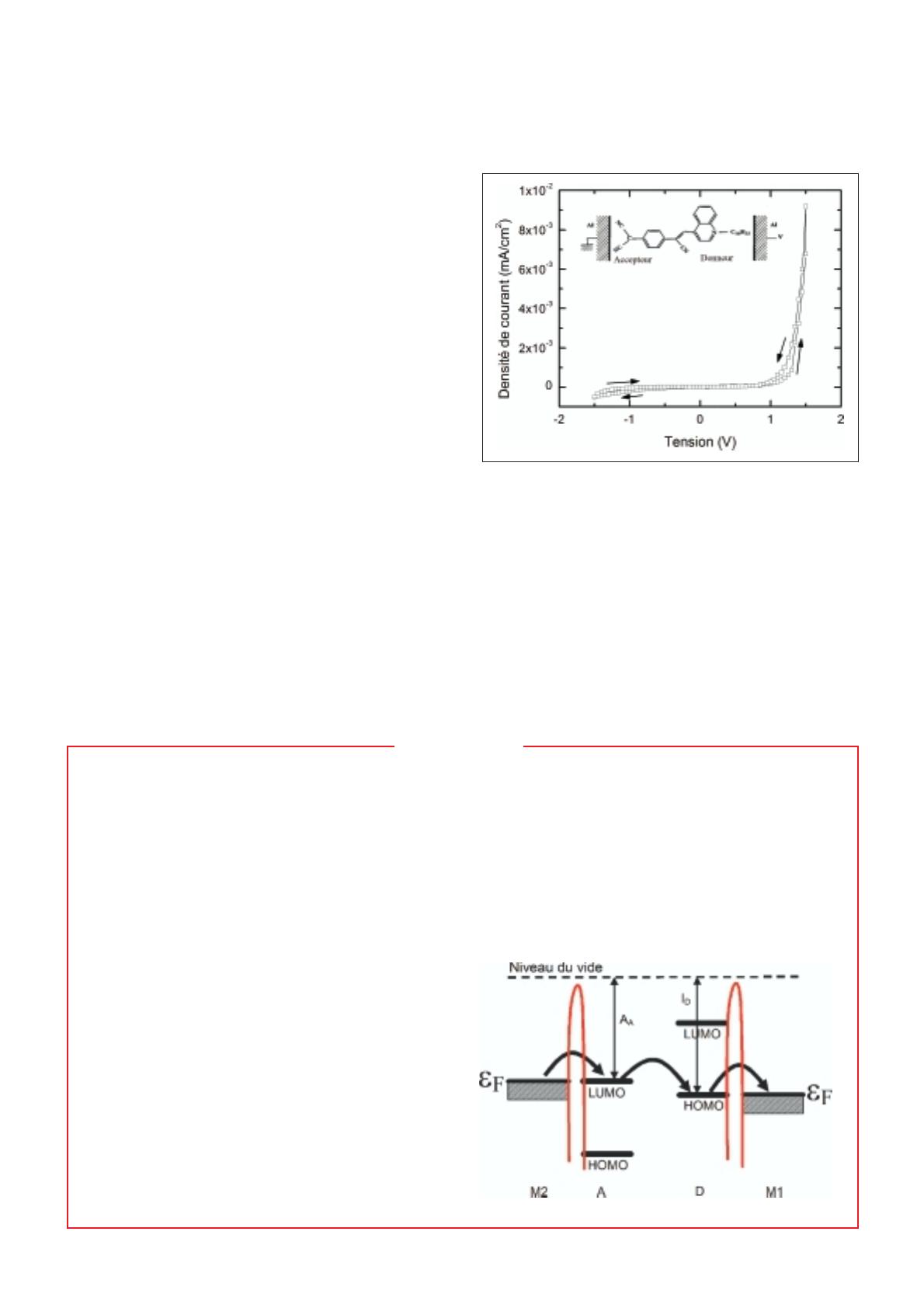
n’en est rien comme le montre notre calcul théorique. Les
orbitales HOMO (dernière orbitale moléculaire remplie
d’électrons, sachant que l’on peuple les orbitales molécu-
laires en commençant par les orbitales moléculaires les plus
basses en énergie) et LUMO (première orbitale moléculaire
vide d’électron) sont délocalisées sur l’ensemble des deux
groupes (figure 2). La conséquence directe de ce résultat est
que la caractéristique courant-tension (calculée par la
méthode des liaisons fortes auto-cohérente) d’une mono-
couche de la molécule Q-3CNQ (le système D-A sans la
chaîne aliphatique) sera symétrique (figure 3-a) donc sans
effet de redressement du courant. Le même calcul avec la
chaîne aliphatique donne quant à lui une caractéristique
asymétrique (figure 3-b) en accord qualitatif avec l’expé-
rience (figure 1). Dans ce cas, c’est l’introduction d’une
asymétrie géométrique dans la structure métal/ molécule/
métal qui est responsable de cet effet de redressement du
courant. Le groupe D-A est en effet mieux couplé électri-
quement avec une électrode qu’avec l’autre, dont il est
séparé par une chaîne aliphatique au caractère d’isolant
électrique. Le potentiel électrique n’est pas réparti de
manière homogène sur toute la molécule, le groupe D-A
n’est soumis qu’à une fraction ηdu potentiel appliqué. En
première approximation, cette fraction s’exprime par
η=1
21+επdσ
εσdπ
où εσ, επ, dσet dπsont respectivement les constantes
diélectriques et les épaisseurs de la partie π-conjugué et de
la chaîne aliphatique de la monocouche de C16H33-Q-
3CNQ.
188
Figure 2 - Représentation de la répartition (en rouge) calculée des densités
d'états des orbitales HOMO et LUMO. Les boules grises représentent les
atomes C, les blanches les H et les bleues les N. Le groupe accepteur est à
gauche, le groupe donneur à droite. Ce calcul montre que les orbitales
HOMO et LUMO sont complètement délocalisées sur toute la molécule.

Quanta et photons
En règle générale, toute asymétrie de couplage de la
molécule avec les deux électrodes est susceptible de
conduire à un tel résultat. Dans le cas de la diode à base de
molécules C16H33-Q-3CNQ, comme la différence d’énergie
EF-EHentre le niveau de Fermi du métal et la HOMO est
plus faible que celle EL-EFentre la LUMO et l’énergie de
Fermi, il est plus facile de mettre en résonance la HOMO
avec le niveau de Fermi du métal pour une tension positive
V+telle que ηeV+~ EF-EH(voir schéma énergétique de
l’encadré 1). Une tension négative plus importante en valeur
absolue serait nécessaire pour la résonance avec la LUMO.
Ce sont ces deux effets, asymétries géométrique et énergé-
tique, qui induisent le comportement redresseur de la jonc-
tion métal/C16H33-Q-3CNQ/métal.
D'autres types de diodes moléculaires
Ces mécanismes d’asymétrie sont généralisables et peu-
vent être exploités pour fabriquer des diodes moléculaires
avec d’autres groupes π-conjugués, en particulier des
groupes plus faciles à synthétiser que la molécule C16H33-
Q-3CNQ. La figure 4 donne une illustration pour une
couche organique auto-assemblée sur un substrat de sili-
cium fortement dopé de type-n (dégénéré). La monocouche
est synthétisée par greffage chimique en séquence, premiè-
rement, des chaînes alkyltrichlorosilanes puis deuxième-
ment par le greffage de la fonction π-conjuguée sur cette
première monocouche. On observe là aussi un bon effet de
rectification du courant (mais pour les tensions négatives, le
groupe π-conjugué étant ici au-dessus de la chaîne contrai-
rement au cas de C16H33-Q-3CNQ) avec des rapports de
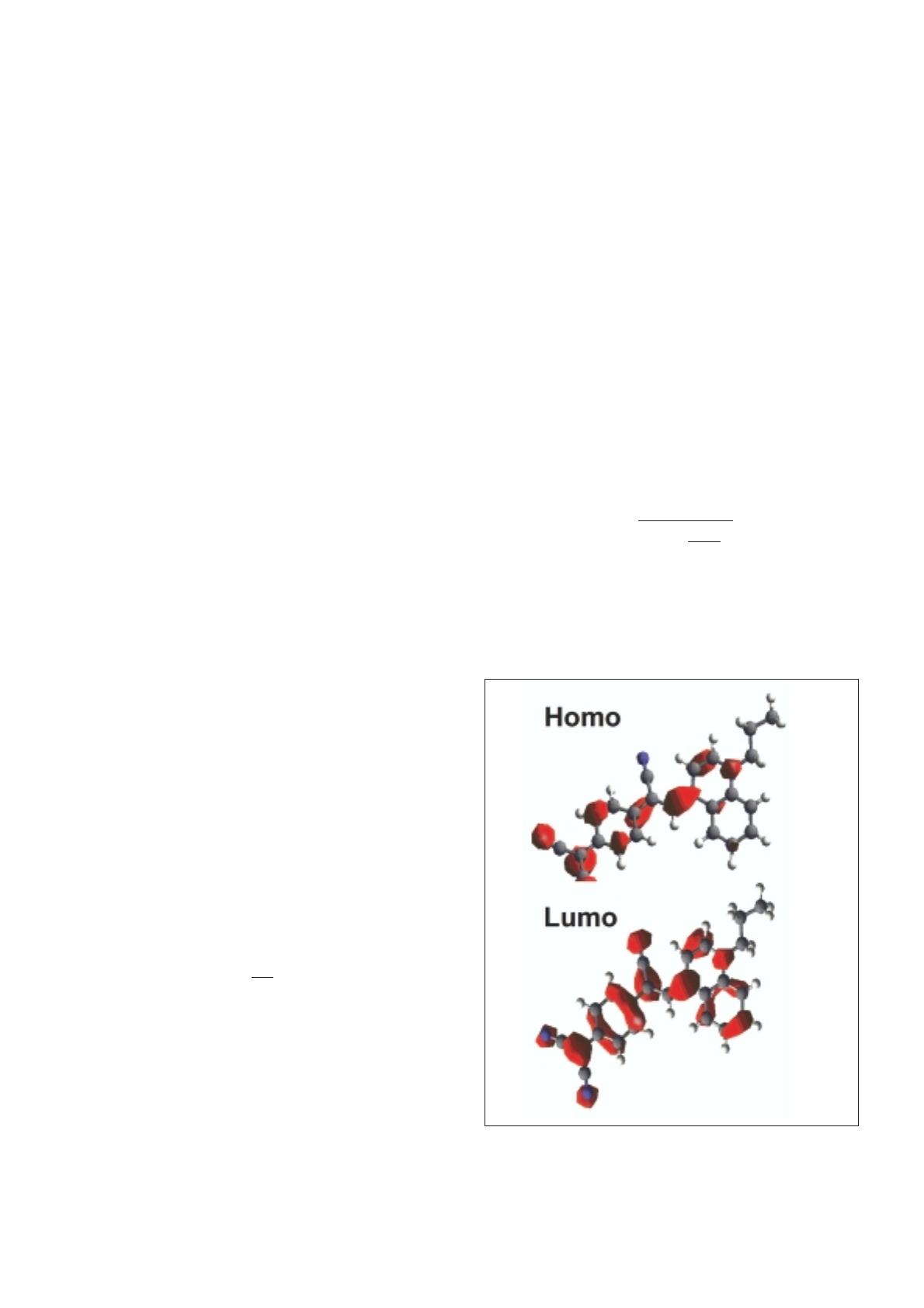
rectification de ~35 et des tensions de seuil de rectification
(VT) de –0.3 à –0.9 V. Nous avons ainsi réalisé des diodes
moléculaires avec des groupes π-conjugués donneurs
simples (phényle, thiophène, pyrène, anthracène,...) plus
faciles à synthétiser et/ou disponibles commercialement, et
pour différentes longueurs de la chaîne alkyle (de 6 à 15
groupes CH2).
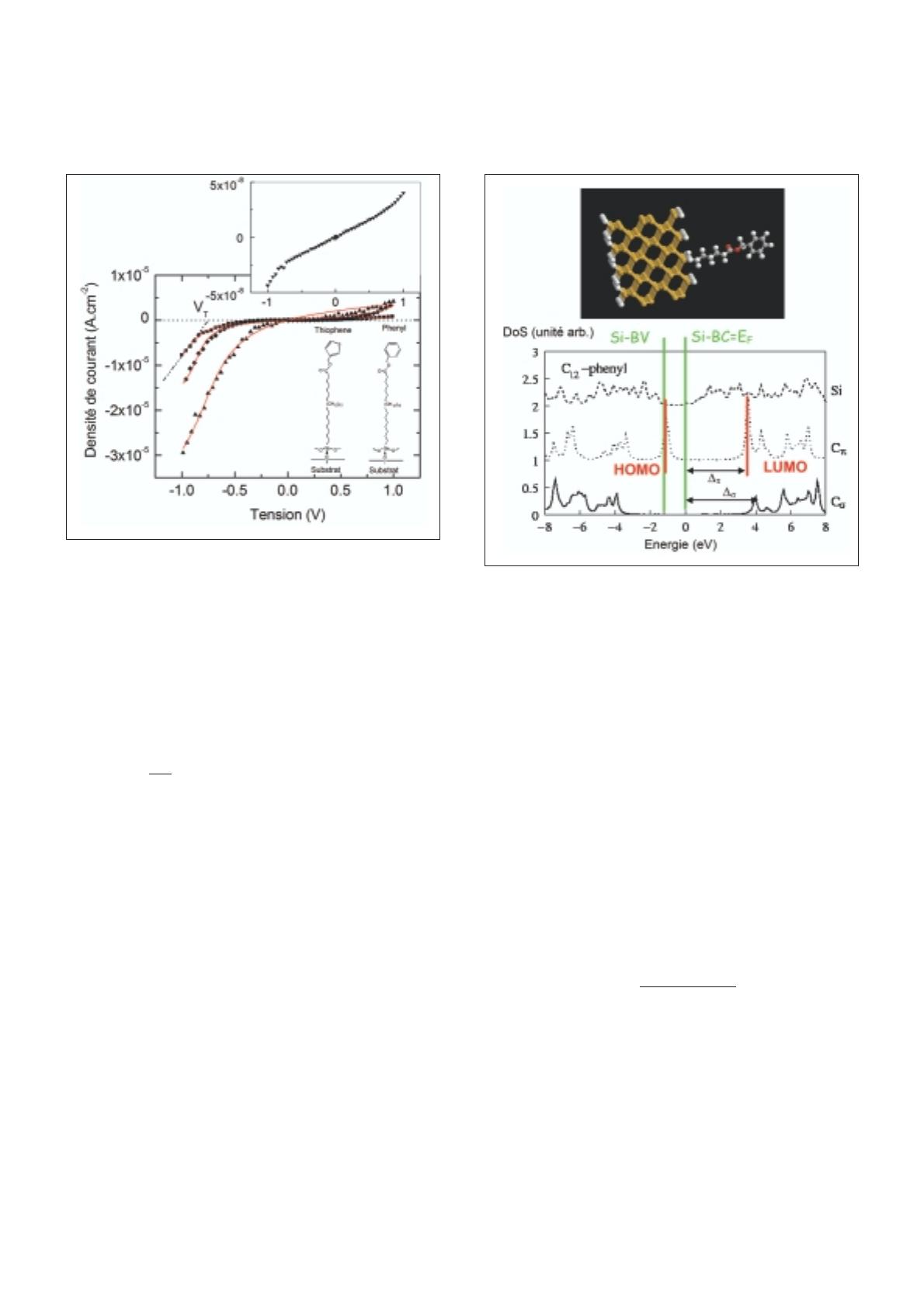
Le calcul de la structure électronique du système silicium
/molécule permet de comprendre là aussi l’origine de ces
effets. La HOMO du groupe π-conjugué (phényle dans
l’exemple de la figure 5) est à ~1.1 eV du niveau de Fermi
du silicium (confondu avec le bas de bande de conduction
pour le silicium n+), alors que la LUMO est à ~3.1 eV. Une
plus faible tension négative sur l’électrode supérieure suffira
pour amener la HOMO en résonance avec le niveau de
Fermi du silicium, alors qu’il faudrait une tension positive
plus importante pour faire de même avec la LUMO. Si on
considère que, dans la gamme de tension mesurée (–2V,
+2V), seule la HOMO participe au transfert de charge dans
la molécule, on peut utiliser un modèle analytique à un
niveau d’énergie pour modéliser les courbes courant-ten-
sion. Ce modèle prévoit que le courant J en fonction de la
tension appliquée V est donné par :
189
Figure 3 - (a) à gauche : cacul de la courbe courant-tension dans le cas d'une jonction étal/Q-3CN/métal et (b) à droite : d'une jonction métal/C16H33-Q-
3CNQ/métal.

J=2J0
πtan−1[θ(E0+ηeV)]
−tan−1[θ(E0−(1−η)eV)]
où E0= EF– EHOMO, ηest le paramètre d’asymétrie donné
précédemment, et θun paramètre de couplage molécule/
électrode.
Ce modèle donne un bon ajustement des courbes expéri-
mentales (figure 4) et nous pouvons comparer les valeurs de
E0issues de l’ajustement à l’expérience (0.6 < E0< 0.9 eV),
avec notre calcul théorique de la position énergétique de la
HOMO du groupe π-conjugué (0.7 eV pour le thiophène et
1.1 eV pour le phényle). L’accord trouvé est raisonnable
compte tenu de la dispersion des résultats expérimentaux et
des simplifications du calcul. Pour aller plus loin dans la
détermination de la structure électronique de ces diodes
moléculaires, nous avons mesuré la position des orbitales
moléculaires par une méthode de spectroscopie de photo-
courant. Pour une tension faible (typiquement 100 mV),
donc hors résonance avec les orbitales moléculaires, on
photo-injecte des charges au-dessus de la barrière d’énergie
que représente la différence entre le niveau de Fermi de
l’électrode et l’orbitale moléculaire. Lorsque l’on balaye
l’énergie des photons excitateurs, un seuil dans la courbe
photocourant donne directement une mesure de la position
de l’orbitale considérée (figure 6). Ce seuil correspond à
l’énergie des photons excitateurs. Pour une jonction
Si-n+/chaîne alkyle/Al (donc sans groupe π-conjugué) on
trouve ainsi ELUMO – EF~ 4.1 eV et EF– EHOMO ~ 5.3 eV
(le gap HOMO-LUMO d’une chaîne alkyle est de ~ 9 eV).
Quand on rajoute le groupe π-conjugué, une barrière
d’énergie plus faible est mise en série avec la précédente.
On mesure alors une barrière moyenne , qui correspond à
la mise en série de deux barrières rectangulaires et qui vaut
dans l’approximation WKB (Wentzel-Kramers-Brilloin)
=σdσ+πdπ
d
où σet πsont les énergies de barrière des parties satu-
rées (chaîne alkyle) et π-conjugué de la molécule, respecti-
vement (dans cette équation, le terme générique corres-
pond à ELUMO-EFquand on considère la LUMO et à
EF-EOMO pour la HOMO). De même, dσet dπsont les lon-
gueurs de ces deux barrières (d=dσ+dπ). A partir de nos
calculs (figure 5), les valeurs σet πsont connues aussi
bien pour la LUMO que pour la HOMO (par exemple, pour
la LUMO, on a σ~ 4.1eV et π~ 3.3eV, figure 5), et nous
pouvons donc en déduire la valeur de (soit ~ 3.9eV en
appliquant l’équation ci-dessus). En présence du groupe
190
Figure 4 - Courbes courant-tension d'une jonction Si-n+/monocouche
σ-π/Al : (π) thiophène-chaîne courte (CH2)6; ( ) phényle-chaîne longue
(CH2)15 ; et ( ) thiophène-chaîne longue (CH2)15. La tension de seuil de
rectification (VT) est marquée dans l'un des cas. En encart, représentation
de la structure moléculaire de deux des jonctions à chaîne longue. La cour-
be courant-tension supérieure correspond à celle d'une jonction témoin
dans le groupe π-conjugué Si-n+/chaîne alkyle/Al, montrant qu'il n'y a pas
alors d'effet de redressement du courant. En rouge : ajustement du modèle.
Figure 5 - Calcul de la densité d'état (DoS) pour un système Si-n+(dégé-
néré)/σ-π(chaîne à 12 carbones σet groupe phényle). Légende : Si = DoS
du silicium ; Cσ= DoS de la chaîne aliphatique, Cπ= DosS du groupe phé-
nyle. Les lignes vertes correspondent à la bande interdite du silicium (BV =
bande de valence, BC = bande de conduction), les lignes rouges montrent
les positions respectives des orbitales HOMO et LUMO déduites de la den-
sité d'état des carbones π. La figure du haut représente le modèle de la
molécule sur le substrat de silicium (C = gris, O = rouge, Si = jaune, H =
blanc).