Chap.2 – Formation des images en optique

1
Chap.2 – Formation des images en optique
1. Systèmes optiques - Notions d’objet et d’image
1.1. Définitions relatives aux systèmes optiques
1.2. Définition d’un objet ponctuel et d’une image ponctuelle
1.3. Objet / image étendus
1.4. Diamètre angulaire d’un objet étendu situé à l’infini
1.5. Objet réel ou virtuel - Image réelle ou virtuelle
1.6. Exemple du miroir plan
2. Conditions nécessaires à la formation d’images : stigmatisme et aplanétisme
2.1. Stigmatisme
2.2. Aplanétisme
3. Former des images nettes : systèmes centrés dans l’approximation de Gauss
3.1. Conditions de Gauss
3.2. Relation de conjugaison - Exemple du miroir plan
Intro :
Un objectif essentiel du programme d’optique de première année est de comprendre comment former des images
de qualité avec les systèmes optiques usuels que sont les lentilles et les miroirs.
On donne dans ce chapitre quelques définitions générales concernant la formation des images. La plupart des
systèmes optiques ne permettent d’obtenir des images nettes que dans les conditions de Gauss, que l’on énoncera.
1. Systèmes optiques - Notions d’objet et d’image
1.1. Définitions relatives aux systèmes optiques
o Système optique : Un système optique  est constitué d’un certain nombre de milieux transparents séparés
par des surfaces réfractantes ou réfléchissantes (généralement des lentilles et des miroirs).
o Système optique centré : Un système optique est dit centré lorsqu’il possède un axe de symétrie de
révolution. Cet axe s’appelle l’axe optique.
o Système dioptrique : Système optique ne comprenant que des dioptres.
o Système catadioptrique : Système optique comprenant des dioptres et des miroirs.
o Système catoptrique : Système ne comprenant que des miroirs.
1.2. Définition d’un objet ponctuel et d’une image ponctuelle
o Objet ponctuel :
Un objet ponctuel est le point d’intersection de rayons lumineux incidents sur le système optique. Un objet
peut aussi se trouver à l’intersection du prolongement des rayons incidents.

2
On notera que ce que l’on nomme ici objet n’a pas nécessairement de réalité matérielle. On fera bien la distinction
entre source de lumière et objet. Une source de lumière « crée » de la lumière, et peut être utilisée comme objet.
Mais un objet n’est pas nécessairement une source de lumière.
o Image ponctuelle :
Une image ponctuelle est le point d’intersection de rayons lumineux émergents du système optique. Une
image ponctuelle peut aussi se trouver à l’intersection du prolongement des rayons émergents
Tous les systèmes optiques ne sont pas capables de former une image ponctuelle à partir d’un objet ponctuel A.
Si tous les rayons incidents issus de A convergent vers un point A’ après traversée du système (S), alors A’ est
l’image de A à travers (S).
Remarque : Les notions « d’objet » et « d’image » n’ont une signification précise que si l’on précis le système
optique dont on parle. En effet, une image A’ formée par une première lentille, peut aussi être l’objet d’une
deuxième image A’’ formée par une seconde lentille.
1.3. Objet / image étendus
Un objet étendu peut être décomposé en un ensemble d’objets ponctuels.
Une image étendue est alors l’ensemble des images ponctuelles formées à partir des points constitutifs de l’objet
étendu.
1.4. Diamètre angulaire d’un objet étendu situé à l’infini
Dans le cas particulier des objets étendus situés à grande distance du système optique, la dimension des objets ne
présente pas un grand intérêt en optique. Par exemple, pour parler de la taille de la Lune vue à l’œil, donner son
diamètre (en mètres) n’est pas pertinent. Il est plus intéressant de connaître son diamètre angulaire, i.e. l’angle
sous lequel la Lune est vue.
Remarque : Un objet est « situé à grande distance » si sa distance au système optique est très grande devant les
distances caractéristiques de ce système (focale d’une lentille, diamètre de la face d’entrée du système, etc.).
Dans les calculs et les schémas, on pourra considérer que l’objet se situe à l’infini.
Remarque : On retiendra que les rayons en provenance d’un objet ponctuel situé à l’infini arrivent sur le système
parallèlement les uns aux autres.
1.5. Objet réel ou virtuel - Image réelle ou virtuelle
o Face d’entrée de (S) : Surface du système frappée par les rayons incidents.
o Face de sortie de (S) : Surface du système d’où sortent définitivement les rayons émergents.
o Espace objet (ou milieu incident) : Portion de l’espace d’où proviennent les rayons incidents.
o Espace image (ou milieu émergent) : Portion de l’espace vers laquelle sortent les rayons émergents.
o Objet réel : Objet se situant dans l’espace objet.
Un objet ne se situant pas dans l’espace objet est un objet virtuel.
o Image réelle : Image se situant dans l’espace image.
Une image ne se situant pas dans l’espace image est une image virtuelle.
NB : Une image virtuelle ne peut pas être observée directement sur un écran. Si l’on ne considère qu’un seul
système optique, une image réelle peut être observée sur un écran.

3
1.6. Exemple du miroir plan
 Identifier les faces d’entrée et de sortie, puis les espaces objet et image d’un miroir plan.
 On place une source ponctuelle devant le miroir. On suppose que la source émet de la lumière dans toutes
les directions de l’espace. En effectuant des tracés de rayons lumineux, trouver la position de son image.
Est-elle réelle ou virtuelle ?
2. Conditions nécessaires à la formation d’images : stigmatisme et aplanétisme
Le but d’un instrument d’optique est de former, à partir d’un objet, une image sur une surface généralement plane
(écran, pellicule photo, etc.).
La première exigence consiste à obtenir une image nette. C’est le cas lorsqu’on peut associer à chaque point de
l’objet une image ponctuelle : c’est la condition de stigmatisme.
La deuxième exigence est d’obtenir une image non déformée de l’objet. Concrètement, on souhaite que l’image
d’un plan orthogonal à l’axe optique soit aussi un plan orthogonal à l’axe optique : c’est la condition
d’aplanétisme.
2.1. Stigmatisme
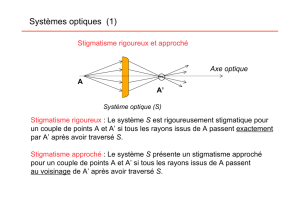
o Stigmatisme rigoureux : Un système optique (S) est dit rigoureusement stigmatique si l’image d’un point est
un point. Deux points images l’un de l’autre à travers ce système sont dits conjugués.
Très peu de systèmes optiques sont rigoureusement stigmatiques pour un grand nombre de couples de points. Le
miroir plan est un cas exceptionnel : il est rigoureusement stigmatique pour tout couple de points symétriques par
rapport au miroir. Autrement dit, tout point objet donne une image ponctuelle à travers le miroir.
Comment peut-on réaliser des systèmes optiques stigmatiques qui n’utilisent pas que des miroirs plans ?
(appareil photo, microscope, lunette astronomique, lunettes de vue, jumelles, œil, etc.)
En réalité, il n’est pas nécessaire qu’un point objet donne rigoureusement une image ponctuelle. En effet, tous les
récepteurs photosensibles (rétine de l’œil, pixel d’une caméra, pellicule photo) possèdent une certaine
« granularité ». L’exemple le plus simple est celui d’une caméra constituée de pixels. Il suffit que l’image formée
sur la caméra soit une tâche de dimension inférieure à la taille d’un pixel pour que le système optique puisse être
considéré comme stigmatique.
o Stigmatisme approché : Un système optique est approximativement stigmatique si l’image d’un point est une
tâche de très petites dimensions devant la granularité du récepteur de lumière.
2.2. Aplanétisme
Un système est dit aplanétique si un plan objet orthogonal à l’axe optique a pour image un plan orthogonal à
l’axe optique. Les plans sont alors conjugués.

4
3. Former des images nettes : systèmes centrés dans l’approximation de Gauss
3.1. Conditions de Gauss
Les systèmes centrés présentent une propriété très intéressante. S’ils sont utilisés dans les conditions de Gauss,
ils sont alors approximativement stigmatiques et aplanétiques.
Un système centré est utilisé dans les conditions de Gauss s’il n’est traversé que par des rayons paraxiaux :
o les rayons atteignent la face d’entrée de (S) proche de l’axe optique
o ils sont peu inclinés par rapport à l’axe optique (<10°)
Dans ces conditions :
 tout point A situé sur l’axe possède un conjugué A’, situé aussi sur l’axe
 tout plan orthogonal à l’axe possède un plan conjugué orthogonal à l’axe
3.2. Relation de conjugaison - Exemple du miroir plan
Lorsqu’un système optique est stigmatique, il existe une ou plusieurs relations mathématiques reliant les positions
des points conjugués sur l’axe optique : ce sont les relations de conjugaison.
Lors de l’étude des systèmes optiques, on utilisera des longueurs algébriques,
après avoir orienté les axes horizontal et vertical selon un sens conventionnel.
 Etablir la relation de conjugaison dans le cas du miroir plan.
Notions clefs
Savoirs :
 Toutes les définitions, le vocabulaire
 Stigmatisme, aplanétisme
 Conditions de Gauss (avec des mots + SCHEMA)