Structures Arborescentes – Implémentations - Algo, la page

Structures Arborescentes – Implémentations
Nathalie Junior Bouquet
avril 2013
1 Arbres binaires
Définition
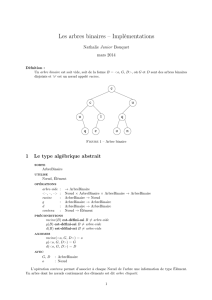
Un arbre binaire est soit vide, soit de la forme B= <o,B1,B2>, où B1et B2sont des arbres
binaires disjoints et ’o’ est un nœud appelé racine.
q
e
u
q
no
c
l
e
u
Figure 1 – Arbre binaire
1.1 Le type algébrique abstrait
sorte
ArbreBinaire
utilise
Nœud, Élément
opérations
arbre-vide :→ArbreBinaire
<–, –, –> : Nœud ×ArbreBinaire ×ArbreBinaire →ArbreBinaire
contenu : Nœud →Élément
racine : ArbreBinaire →Nœud
g: ArbreBinaire →ArbreBinaire
d: ArbreBinaire →ArbreBinaire
préconditions
racine(B1)est-défini-ssi B1̸=arbre-vide
g(B1)est-défini-ssi B1̸=arbre-vide
d(B1)est-défini-ssi B1̸=arbre-vide
axiomes
racine(<o,B1,B2>) = o
g(<o,B1,B2>) = B1
d(<o,B1,B2>) = B2
avec
B1,B2: ArbreBinaire
o: Nœud
1

Algorithmique
Types abstraits : Les arbres – avril 2013
Info-Sup
Epita
L’opération contenu permet d’associer à chaque Nœud de l’arbre une information de type Élément. Un
arbre dont les nœuds contiennent des éléments est dit arbre étiqueté.
On notera, abusivement, <r,G,D> l’arbre dont la racine contient l’élément r.
D
r
G
Figure 2 – Arbre binaire : une structure récursive
1.2 Représentation dynamique
La représentation la plus naturelle reproduit la structure récursive (voir figure 2).
On utilise les pointeurs pour chaîner entre eux les nœuds. A chaque nœud on associe deux pointeurs,
vers les deux sous-arbres gauche et droit. L’arbre non vide est représenté par un pointeur sur le nœud
racine. Il a la valeur nul s’il est vide.
Nous utiliserons la plupart du temps des arbres étiquetés. Un champ supplémentaire cle contiendra
l’information contenue dans le nœud.
1.2.1 Le type
types
/* déclaration du type t_element*/
t_arbreBinaire = ↑t_noeudBinaire
t_noeudBinaire = enregistrement
t_element cle
t_arbreBinaire fg, fd
fin enregistrement t_noeudBinaire
e
B
NUL
NULNUL
NUL
NUL
NULNULNULNUL
NUL
NUL
uq
c
q e
l
o n
u
Figure 3 – Représentation dynamique de l’arbre de la figure 1
2

Algorithmique
Types abstraits : Les arbres – avril 2013
Info-Sup
Epita
1.2.2 Implémentation des opérations
Type abstrait : ArbreBinaire Implémentation : type t_arbreBinaire
B: ArbreBinaire B : t_arbreBinaire
arbre-vide nul
contenu(racine(B)) B↑.cle
g(B) B↑.fg
d(B) B↑.fd
1.3 Représentation statique
On peut simuler la représentation précédente à l’aide de tableaux 1: les pointeurs sont alors remplacés
par des entiers indiquant les positions des nœuds dans le tableau. L’arbre est représenté par le tableau,
ainsi qu’un entier indiquant la position de la racine.
1.3.1 La numérotation hiérarchique
On peut utiliser un simple vecteur pour représenter un arbre binaire. Il suffit de stocker chaque nœud
à la position correspondant à sa numérotation hiérarchique.
10
i
a t
f
r
a
p
_
n
u
1
2 3
4 5 6 7
8 9
Figure 4 – Arbre binaire parfait + numérotation hiérarchique
constantes
nbMAxNoeuds = ...
types
/* déclaration du type t_element*/
t_AB_Hierarchique = nbMAxNoeuds t_element
variables
t_AB_hierarchique B
L’arbre de la figure 4 sera représenté par le tableau suivant :
1 2 3 4 5 6 7 8 9 10
f p i n r a t u _ a
1. Selon le même principe que pour les ”fausses listes chaînées“
3

Algorithmique
Types abstraits : Les arbres – avril 2013
Info-Sup
Epita
L’utilisation de cette représentation est intéressante sur un arbre parfait (ou complet, comme celui de
la figure 8), car on peut limiter la taille du vecteur à celle de l’arbre. Par contre, sur un arbre quelconque,
la place occupée n’est plus optimisée.
Représentation de l’arbre de la figure 1 :
1 2 3 4 5 6 7 8 9 10 11 12 13
e c u u l q q e o n
La place occupée sera d’autant moins optimisée que la hauteur de l’arbre sera élevée. Dans le cas d’un
arbre dégénéré (ou filiforme) à nnœuds, l’espace occupé peut alors atteindre 2n−1!
f
e
f
i
l
i
Figure 5 – Arbre filiforme Figure 6 – Peigne droit
Représentation de l’arbre filiforme de la figure 5 :
1 2 3 . . . 7 . . . 14 . . . 29 . . . 58
f i . . . l . . . i . . . f . . . e
Représentation du peigne droit de la figure 6 :
1 2 3 . . . 6 7 . . . 14 15 . . . 30 31 . . . 62 63
p d e . . . r i . . . o g . . . i n . . . t e
1.3.2 Utilisation
◦La racine est en position 1 dans le vecteur.
◦Si iest la position du nœud actuel alors :
◃son fils gauche se trouve à la position 2i
◃son fils droit se trouve à la position 2i+ 1
◃son père (sauf pour la racine de l’arbre),
se trouve à la position idiv 2.
En pratique, il faut avoir une valeur particulière (∅)
pour remplacer la racine de l’arbre vide. Sauf si
l’arbre est parfait : la taille de l’arbre suffit !
4

Algorithmique
Types abstraits : Les arbres – avril 2013
Info-Sup
Epita
1.4 Parcours d’un arbre binaire
1.4.1 Parcours en profondeur
Le parcours en profondeur main gauche consiste à
descendre dans l’arbre à gauche le plus loin possible.
Lorsque l’on ne peut plus aller à gauche, on descend à
droite. Lorsqu’on ne peut plus descendre, on remonte
d’un niveau : si on vient de la gauche, on descend à
droite, sinon on remonte encore. . .
La manière la plus simple d’envisager ce parcours est récursive. Il revient tout simplement à parcourir
le sous-arbre gauche, puis à parcourir le sous-arbre droit !
DG
r
(1) : préfixe (2) : infixe (3) : suffixe
(3)
(2)
(1)
Figure 7 – Parcours en profondeur d’un arbre binaire
Lors du parcours en profondeur, chaque nœud est rencontré trois fois :
(1) avant de descendre sur le sous arbre-gauche : ordre préfixe,
(2) en remontant de la gauche, avant de descendre à droite : ordre infixe (ou symétrique),
(3) en remontant de la droite : ordre suffixe (ou postfixe).
Exemples : les trois ordres de traitement des nœuds d’un arbre induits lors d’un parcours en profondeur.
◦L’ordre préfixe sur l’arbre de la figure 8 donnera : lui_est_complet
◦L’ordre infixe sur l’arbre de la figure 4 donnera : un_parfait
◦L’ordre suffixe sur l’arbre de la figure 1 donnera : quelconque
m te
l
p
o
c
_te_
i
u
l
s
Figure 8 – Arbre binaire complet
5