analogique et analogique-numérique

Denis Rabasté IUFM Aix Marseille 1/1
Technologie des circuits liés aux conversions numérique-
analogique et analogique-numérique
Le développement des techniques d'intégration à grande échelle a permis la réalisation de circuits
numériques de plus en plus complexes et de plus en plus rapides. Les informations traitées étant la
plupart du temps d'origine analogique, il s'ensuit une demande importante de convertisseurs qui sont
utilisés dans de nombreux domaines.
Dans le cas d’une conversion de l’analogique vers le numérique, le signal analogique est « observé »
à intervalles de temps fixe ; on parle d’échantillonnage. Plus le signal analogique varie rapidement,
plus la fréquence d’échantillonnage devra être importante, et plus le convertisseur analogique
numérique (CAN ou ADC pour « analog to digital converter ») devra être rapide.
A chaque instant d’échantillonnage, la valeur du signal analogique est convertie en valeur binaire sur
un nombre de bits dépendant de la précision requise pour l’application. Plus le nombre de bits est
important, meilleure est la résolution, et plus précis devra être le CAN.
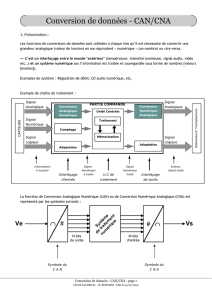
Le produit "nombre de bits - fréquence d'échantillonnage" est limité par le savoir-faire technologique
comme le montre la diagonale sur la caractéristique suivante où sont répertoriées les principales
applications.
fréquence
d'échantillonnage
nombre
de bits
audio
télécommunication
sonars
radars
mesures
TV et radio numérique
oscilloscope
numérique
1 GHz1 MHz
8
12
16
24
1 kHz
La vitesse de commutation des composants limitera la vitesse tandis que les différentes erreurs
(tolérance des composants, tension de décalage des amplificateurs) limiteront la précision. Le
problème est identique que l’on considère un CAN ou un CNA (convertisseur numérique analogique
ou DAC pour « digital to analog converter »).
Pour comprendre les problèmes de précision, il faut être conscient du fait, pour prendre un exemple
extrême, qu'un convertisseur 24 bits de 10 V pleine échelle doit être capable de traiter des tensions à
10/224=0,6 µV près.
1. Caractéristiques idéales et réelles
La figure ci-après représente la caractéristique idéale d'un convertisseur analogique-numérique (CAN)
et celle que l’on obtient réellement avec un circuit limité en résolution (ici deux bits afin de simplifier la
figure).
Dans le cas d’un convertisseur idéal (nombre de bits infini), il faut alors considérer la graduation de
l’axe des ordonnées comme les deux bits de poids fort d’une suite infinie.

technologie des circuits liés aux conversions numérique-analogique et analogique-numérique
Denis Rabasté IUFM Aix Marseille 2/2
sortie
numérique
tension
pleine échelle
caractéristique
idéale
CAN
2 bits
tension d'entrée
analogique
caractéristique
réelle
00
01
10
11 q
Le quantum q est défini comme la plus petite variation de la tension analogique produisant une
variation du code numérique, d'où :
q= tension analogique pleine échelle crête à crête
2
N
où "N" est le nombre de bits du convertisseur, 1/2N étant appelé la résolution du convertisseur.
Il existe une confusion fréquente entre ces deux termes "N" étant souvent désigné comme la
résolution par les constructeurs.
De même le quantum est souvent désigné par le terme LSB (Leat Significant Bit : bit de plus faible
poids) par référence à la correspondance qui existe entre ces deux notions.
Plus le quantum sera grand (donc plus le nombre de bit sera faible) et plus l’erreur, dite de
quantification, entre la valeur à l’entrée du CAN et celle numérisée sera grande.
Pour un nombre de bit fixé, l’erreur relative due à la quantification est plus importante si le signal
analogique est faible. C’est la raison pour laquelle, la caractéristique du CAN est décalée d’un demi-
quantum sur la gauche, comme le montre la figure suivante dans le cas d’un convertisseur 3 bits ; afin
de récupérer l’intégralité de la tension pleine échelle, le demi-quantum manquant est rajouté à droite
de la caractéristique.
sortie numérique
tension pleine échelle
caractéristique
idéale
CAN
3 bits
tension d'entrée
analogique
caractéristique
réelle
000
001
010
011
100
101
110
111
Pour un convertisseur numérique-analogique (CNA), on obtient une caractéristique réelle composée
de points, les valeurs intermédiaires ne pouvant être fournies par la partie numérique, comme le
montre la figure suivante.
On peut constater, sur la figure de gauche dans le cas simple d’un convertisseur 2 bits, que
l’expression du quantum est alors la tension pleine échelle divisée par 2n-1.
Dans le cas d’un convertisseur réel, toujours pour diminuer l’erreur relative de quantification pour les
faibles valeurs, que la caractéristique réelle est décalée d’un demi-quantum vers la gauche, comme
on le voit sur la figure suivante à gauche.

technologie des circuits liés aux conversions numérique-analogique et analogique-numérique
Denis Rabasté IUFM Aix Marseille 3/3
entrée
numérique
tension
pleine
échelle caractéristique
idéale
CNA
2 bits
tension de sortie
analogique
caractéristique
réelle
00 10 11
q
01
entrée
numérique
tension
pleine
échelle
caractéristique
idéale
CNA
3 bits
tension de sortie
analogique
caractéristique
réelle
000 001 010 011 100 101 110 111
q
Les caractéristiques présentées ici concernent des convertisseurs unipolaires, la tension analogique
n’étant pas négative. Pour un convertisseur bipolaire (tension analogique positive ou négative), les
caractéristiques deviennent alors :
000
001
010
011
100
101
110
111
sortie
numérique
entrée
analogique
CAN
bipolaire
3 bits
000 001 010 011 100 101 110 111
sortie
analogique
entrée
numérique
CNA
bipolaire
3 bits
Le codage utilisé par les convertisseurs est le binaire naturel dans le cas d'une conversion unipolaire
et le binaire décalé dans le cas d'une conversion bipolaire (ce qui simplifie la structure du
convertisseur).
2. Rappel des principaux résultats de la théorie de l'échantillonnage
2.1. Fréquence d'échantillonnage
L’échantillonnage d’un signal peut être vu mathématiquement comme la multiplication du signal par
une suite d’impulsion à la fréquence d’échantillonnage (suite d’impulsions appelée « peigne de
Dirac »). Lorsque l’on souhaite restituer ce signal après un éventuel traitement, le CNA va « bloquer »
les valeurs des impulsions pour obtenir un signal en marche d’escalier, qui sera ensuite lissé par un
filtre passe-bas.
La figure suivante nous montre l’exemple d’un signal sinusoïdal de 1 kHz (période 1 ms) échantillonné
à 16 kHz. Le signal quantifié, qui n’est qu’une suite de nombres, n’a pas été représenté.

technologie des circuits liés aux conversions numérique-analogique et analogique-numérique
Denis Rabasté IUFM Aix Marseille 4/4
0 1e-3 2e-3 3e-3 4e-3 5e-3
-5
-4
-3
-2
-1
0
1
2
3
4
5
0 1e-3 2e-3 3e-3 4e-3 5e-3
-5
-4
-3
-2
-1
0
1
2
3
4
5
signal entré, peigne de Dirac
temps (s)
amplitude (V)
0 1e-3 2e-3 3e-3 4e-3 5e-3
-5
-4
-3
-2
-1
0
1
2
3
4
5signal échantillonné
temps (s)
amplitude (V)
0 1e-3 2e-3 3e-3 4e-3 5e-3
-6
-4
-2
0
2
4
6signal bloqué
temps (s)
amplitude (V)
0 1e-3 2e-3 3e-3 4e-3 5e-3
-5
-4
-3
-2
-1
0
1
2
3
4
5signal de sortie filtré
temps (s)
amplitude (V)
Le théorème de Shannon Nyquist nous indique qu’afin de pouvoir restituer le signal, la fréquence
d’échantillonnage doit être au moins deux fois supérieure à la fréquence maximale du signal
numérisé.
La figure suivante donne l’exemple d’un signal sinusoïdal de 12 kHz échantillonné à 16 kHz ; le
théorème n’étant pas respecté ; on peut constater que le signal restitué n’est pas le même que celui
numérisé.
0 2e-4 4e-4 6e-4 8e-4 10e-4 12e-4 14e-4
-5
-4
-3
-2
-1
0
1
2
3
4
5
0 2e-4 4e-4 6e-4 8e-4 10e-4 12e-4 14e-4
-5
-4
-3
-2
-1
0
1
2
3
4
5
signal entré, peigne de Dirac
temps (s)
amplitude (V)
0 2e-4 4e-4 6e-4 8e-4 10e-4 12e-4 14e-4
-5
-4
-3
-2
-1
0
1
2
3
4
5signal échantillonné
temps (s)
amplitude (V)
0 2e-4 4e-4 6e-4 8e-4 10e-4 12e-4 14e-4
-6
-4
-2
0
2
4
6signal bloqué
temps (s)
amplitude (V)
0 2e-4 4e-4 6e-4 8e-4 10e-4 12e-4 14e-4
-5
-4
-3
-2
-1
0
1
2
3
4
5signal de sortie filtré
temps (s)
amplitude (V)

technologie des circuits liés aux conversions numérique-analogique et analogique-numérique
Denis Rabasté IUFM Aix Marseille 5/5
Il est donc absolument nécessaire d'éliminer du signal d'entrée d'un CAN, toute fréquence ne
satisfaisant pas la condition de Shannon, par un filtre passe bas dit "filtre anti-repliement".
Analogie
Un exemple de sous échantillonnage peut être observé sur une roue de voiture roulant rapidement la
nuit, éclairée par les lampadaires urbains (éclaire à 100 Hz) : la roue semble tourner à l’envers. On
observe la même chose au cinéma (24 images/s) avec les diligences des westerns.
3. Principaux CAN
De nombreuses structures de CAN existent, certaines favorisant la rapidité, d’autres la résolution,
certaines extrêmement complexes, d’autres faisant appel a des concepts pointus en traitement du
signal. Passons en revue quelques exemples simples.
3.1. Convertisseur parallèle ou "flash"
Comme son nom l'indique ce convertisseur est le plus rapide. C'est aussi le plus facile à comprendre.
Une tension de référence alimente un pont de résistances, chaque tension de sortie du pont
correspondant à la précédente augmentée d'un quantum. Le signal à convertir est comparé à tous
ces niveaux par des comparateurs dont les sorties vont passer au niveau logique 1, du plus bas
jusqu'à celui dont la sortie du pont correspond à la valeur du signal incident. Un système combinatoire
convertit alors la valeur dans le code désiré.
+
-
+
-
+
-
+
-
tension
de référence entrée analogique
décodeur
sorties
numérique
R/2
R
R
R
R/2
La rapidité de conversion se paye par une complexité importante : pour un convertisseur N bits il faut
2N-1 comparateurs. Ce principe est donc réservé aux convertisseurs rapides de faible précision. Les
convertisseurs utilisant ce principe on généralement 8 bits et peuvent fonctionner à 100 M ech/s
(108 échantillons par secondes ou 100 Meps ou 100 M sps pour « mega samples per seconds »).
Analogie
Ce mode de fonctionnement est comparable à un thermomètre à mercure dont la hauteur de mercure
serait convertie en binaire ? mentalement par un observateur. La température a un rôle similaire à la
tension analogique, la hauteur de mercure à celui du nombre de 1 successif en sortie des
comparateurs, et l’observateur à celui du système combinatoire de décodage.
3.3. CAN à approximations successives
Le principe consiste à faire circuler un NL1 dans un registre (dit registre à approximations
successives) du poids fort vers le poids faible ; la valeur numérique en sortie du registre est convertie
en analogique par un CNA.