Chap5 ondes sonores

PHYSIQUE
Partie 2- Physique ondulatoire
Chapitre-4
CHAPITRE 5 : Ondes sonores
Pour décrire les sons, les musiciens leur associent des caractéristiques telles que la hauteur, le timbre et
l’intensité. Nous allons étudier les grandeurs physiques qui permettent de définir un son et considérer leurs effets
sur notre perception auditive.
I- Sons et ultrasons
La vibration d'un émetteur sonore, comme celle d'un haut-parleur, engendre une suite de compressions et de
dilatations de l'air qui se propage jusqu'à un récepteur (comme une oreille)
Une onde sonore est une suite de compressions et de dilatations du milieu de propagation qui se propage. Elle
nécessite un support matériel et ne se propage pas dans
le vide. C'est une onde mécanique progressive.
L'oreille humaine perçoit des ondes sonores dont les
fréquences sont comprises entre 20 Hz et 20 kHz. Les
ondes sonores de fréquences inférieures à 20 Hz sont
les infrasons et celles de fréquences supérieures à
20 kHz sont les ultrasons.
Remarque : Certains animaux utilisent les ultrasons : les chauves-souris, les dauphins émettent et perçoivent des
ultrasons dont la fréquence peut être supérieure à 100 kHz pour explorer leur environnement ; les éléphants et les
baleines émettent et perçoivent des infrasons pour communiquer.
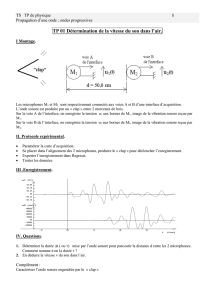
II- Analyse spectrale (voir TP)
L'onde sonore produite par un diapason est une onde sinusoïdale : on dit que le son est pur.
L'onde correspondant au son d'une voix ou d'un instrument de musique est une onde périodique mais n’est pas
sinusoïdale. Le son est complexe.
En 1822, le mathématicien français Joseph Fourier a montré que tout signal périodique de fréquence f1 peut être
décomposé en une somme de signaux sinusoïdaux (sons purs) de fréquences fn multiples de f1.
Ces signaux sinusoïdaux (purs) sont appelés harmoniques. Le son pur de fréquence f1 est appelé fondamental.
(c'est aussi la fréquence du son complexe).
L’analyse spectrale d’un son permet d’en obtenir le spectre en fréquences, une représentation graphique de
l’amplitude de ses composantes sinusoïdales en fonction de la fréquence.
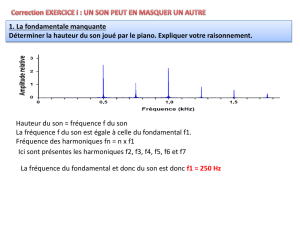
Exemple : Le spectre en fréquences du son (mi4)
d’une guitare montre plusieurs pics de fréquences : à 659
Hz, à 1,32 kHz, à 198 kHz et à 2,64 kHz. Ces fréquences
sont celles des harmoniques, la fréquence la plus faible, f1,
étant celle du fondamental – c’est aussi la fréquence (ou
hauteur) du son. Toutes les fréquences fn du spectre sont
des multiples de la fréquence du fondamental :

PHYSIQUE
Partie 2- Physique ondulatoire
Chapitre-4
Sur l’oscillogramme, on vérifie que 4T = 6,1 ms donc que T = 1,5 ms et que f ~ 660 Hz.
III- Hauteur et timbre
La hauteur et le timbre sont deux caractéristiques importantes d'un son musical.
 Plus la fréquence d'un son est faible, plus le son est
grave. Plus elle est élevée, plus le son est aigu. Si les
fréquences de deux sons musicaux sont différentes, alors ils
sont perçus à des hauteurs différentes.
 Deux sons de même hauteur émis par deux
instruments différents ne sont pas perçus de la même
manière, car les harmoniques sont différents. Ces
instruments ont des timbres différents.
L'analyse spectrale d'un son donne des informations sur :
• la hauteur du son, liée à la fréquence f1 du
fondamental
• le timbre du son, lié au nombre et à l’amplitude
des harmoniques
IV- Intensité sonore et niveau d'intensité sonore
Nous percevons les sons de manière plus ou moins intense.
L’intensité sonore I caractérise l’intensité du signal reçu par l’oreille. Elle s’exprime en W.m–2.
L’oreille humaine perçoit des signaux sonores dont l’intensité est comprise entre une valeur minimale Io = 1,0.10–12
W.m–2 (seuil d’audibilité) et une valeur maximale égale à 25 W.m–2 (seuil de douleur).
On a créé une autre grandeur, le niveau d’intensité sonore, plus aisée à exploiter que l’intensité sonore. Il est noté
L (comme level, « niveau » en anglais) , il est défini à l’aide d’une échelle logarithmique :
𝐿 = 10log 𝐼
𝐼0
où Io est l’intensité au seuil d’audibilité. L s’exprime en
décibels (dB). Son échelle est graduée de 0 à 140 dB
environ, alors que l’intensité sonore est graduée de 10–12 à
102 W.m–2.
Lorsque plusieurs instruments de musique jouent ensemble,
lors d’un concert par exemple, les intensités sonores dues à
chaque instrument s’ajoutent, mais pas les niveaux
d’intensité
sonore.

PHYSIQUE
Partie 2- Physique ondulatoire
Chapitre-4
Application :
Un saxophone joue une note en continu. L'intensité sonore mesurée est I = 10-6 W.m-2. Calculer le niveau sonore
du son.
Réponse : L = 60 dB
Un sonomètre mesure maintenant le niveau sonore d'un deuxième instrument L = 57 dB. Calculer l'intensité sonore.
Réponse : I = 5×10-7 W.m-2.
Conclusion : que se passe t-il quand on double l'intensité sonore ?
Réponse : quand on double l'intensité sonore on augmente de 3dB le niveau sonore
V- Effet Doppler
Intro animation cea :
Le son d’un moteur ou d’une sirène est perçu
plus aigu quand le véhicule qui l’émet s’approche
d’un observateur et plus grave quand il
s’en éloigne. Ce phénomène a été prévu par
Doppler en 1842 puis confirmé
expérimentalement par Ballot en 1845.
Une onde (sonore mais plus généralement
mécanique ou électromagnétique) émise avec
une fréquence fE est perçue avec une
fréquencefR différente lorsque l’émetteur et
le récepteur sont en déplacement relatif:
c’est l’effet Doppler.
Pourquoi, lorsque l'émetteur s’approche de l’observateur, le son de la sirène est-il perçu plus aigu ?
 Lorsque l'émetteur s’approche, la
longueur d’onde perçue par
l’observateur est plus petite que la
longueur d’onde émise : lA < l.
Mathématiquement, on a alors
et a l’inverse fA > f E : la fréquence
reçue
est plus élevée que la fréquence émise, le
son est donc perçu plus aigu.
 De façon analogue, on peut montrer que,
lorsque l'émetteur s'éloigne du
récepteur, le son perçu est plus grave.

PHYSIQUE
Partie 2- Physique ondulatoire
Chapitre-4
1) VITESSE RELATIVE D’UN EMETTEUR PAR RAPPORT A UN RECEPTEUR
La comparaison entre la fréquence fR de l’onde perçue et la
fréquence fE de l’onde émise permet, par exemple, de
déterminer la valeur de la vitesse de l’émetteur par rapport
au récepteur.
Soit une source qui se déplace à la vitesse vE en direction
d’un observateur fixe. Elle émet des ondes périodiques, de
période TE, se propageant dans le milieu à la célérité c.
A une date t1 = 0, la première période de l’onde est émise,
lorsque la source est à la distance D de l’observateur.
Celui-ci la reçoit à la date :𝑡2=𝐷
𝑐
La seconde période de l’onde est émise à la date t3 = TE. La
source se déplaçant
à la vitesse vE, a parcouru pendant ce temps TE, la distance
d = vE x TE.
Par conséquent, cette source ne se trouve plus à la distance
D de l’observateur fixe, mais à une distance D - vE x TE de
l’obsrvateur (puisqu’elle s’est rapprochée).
Le temps mis par la seconde période de l’onde qui se déplace
à la célérité c,
pour arriver à l’observateur fixe qui se trouve à une distance D - vE x TE est donc
L’observateur fixe perçoit donc la seconde période de l’onde, à l’instant
Pour l’observateur la période est alors :
soit une fréquence perçue
On peut montrer alors que la vitesse vE de l’émetteur, correspond pour l’observateur A à une vitesse :

PHYSIQUE
Partie 2- Physique ondulatoire
Chapitre-4
On peut donc ainsi calculer la vitesse vE à partir de la mesure de la fréquence perçue par l’observateur.
On peut reprendre les calculs précédents par rapport à l’observateur B, pour qui l’ambulance s’éloigne.
Remarques. Le calcul précédent suppose :
 L’air est immobile par rapport au sol ;
 La vitesse de déplacement de l’émetteur par rapport au récepteur est faible et très inférieure à la vitesse
de l’onde dans le milieu de propagation.
2) LES APPLICATIONS.
 Les radars routiers utilisent l’effet Doppler avec des ondes
électromagnétiques pour mesurer la valeur de la vitesse des véhicules. Leur
fonctionnent est différent de l’exemple de l’ambulance, car ils sont à la fois
émetteur et récepteur de l’information.
 En imagerie médicale, la valeur de la
vitesse de déplacement du sang peut être mesurée
par effet Doppler. L’écho doppler permet de visualiser le trajet des artères, leurs parois,
leur lumière (diamètre) et la présence éventuelle de rétrécissements, dilatations, de
caillots. Cet examen est particulièrement indiqué dans la maladie athéromateuse. Un écho
doppler sera demandé par exemple face à des signes évoquant une ischémie : des
douleurs des membres inférieurs apparaissant à la marche (signes d’une mauvaise
circulation artérielle au niveau des membres inférieurs), des troubles de la vue, une perte
de connaissance (qui seraient les signes d’une mauvaise circulation au niveau des artères
allant au cerveau). Il est possible d’explorer les artères des membres inférieurs, celles des membres supérieurs,
l’aorte et ses branches cervicales ainsi que les artères intra crâniennes par
des techniques transcrâniennes.
 Mais la plus grande application de l’effet Doppler est en astronomie.
En effet, le spectre de la lumière émise par une étoile comporte des raies
d’absorption caractéristiques des éléments de son atmosphère.
Or lorsqu’on observe le spectre d’une étoile ou d’une galaxie loin de
la Terre, on observe un décalage des raies d’absorption vers les
grandes longueurs d’onde (vers le rouge pour les raies du visible); ce