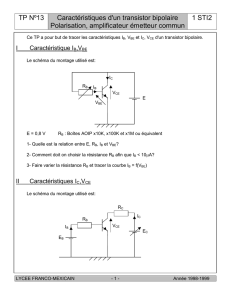
TD2_correction - Faculté des Sciences Rabat

1
Université Mohammed V Electronique Analogique 2011/2012
Faculté des Sciences, Rabat, Agdal IEA SMP5
Exercice 1 :
50 0,98
1
Les résistances sont en
k
et les courants dans les équations sont en
mA
a)
3,3 6 0
61,6
3,3 0,98 1,568
E BE
BE
E
C E C E
I V
V
I mA
I I I I mA
Maille de sortie :
3,3 4,7 20 0
3,3 4,7 20
(3,3 4,7 ) 20
7,6
E CE C
CE E C
E
I V I
V I I
I
V
0,7 7,6 6,9 0
BC BE CE
V V V V      
0
BC
V
, le transistor est effectivement en mode actif direct.
b) On suppose que le transistor est en mode actif normal, on a :
6 3,3 0
61,6
3,3 0,98 1,568
BE E
BE
E
C E C E
V I
V
I mA
I I I I mA
Calcul de
CE
V
10 4,7 3,3 0
10 (4,7 3,3 )
2,44
C CE E
CE C
V I V I
V V I
V

2
6
10 4,7
10 4,7 1,568
2,63
B
C C
V V
V I
V
0
CB
V
, le transistor est donc en saturation, la tension
0,2
EC ECsat
V V V
0,2 6 0,7 0,2 5,5
E
C E
V
V V V       
5,5 ( 10) 0,957
4,7
C
I mA
1,6 0,957 0,643
B E C
I I I mA    
c) On suppose que le transistor est en mode normal :
0,7 0
0,7
3,3 0,21
3,3
0 0
10 4,7 0
EB E B
E E E
C E B
CB C C
V V V
V I I mA
I I I
V V I
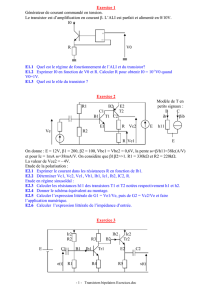
d)
3.3k
3.3k
10V
100k
10V
10k
1
I
c
I
1
( )
c
I I
1
( )
B
I I
B
I
BE
V
Loi des mailles :
1 1
1
3,3( ) 100 10 0
10( ) 0
C BE
C
BE
I I V I
I
V I
1
1
103,3 3,3 10
10
10
C BE
C BE
I I V
I I V

3
1100 0,1( 100 33 ) 0,385
33 1033
100 113,3 0,077
33 1033
BE
BE
C
V
I mA
V
I mA
Calcul de
CE
V
1
1
3,3( ) 3,3 10 0
3,3 6,6 10 7,198
C CE C
CE C
I I V I
V I I V
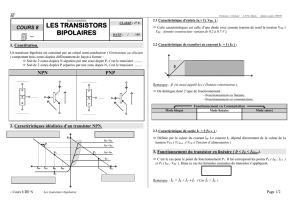
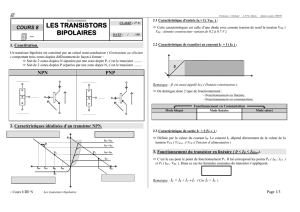
Exercice 2 :
1) A la sortie, on peut écrire :
0
( )
E E CE C C CC
CE CC E C C
C E
R I V R I V
V V R R I
I I
L’équation ci-dessus est l’équation de la droite de charge
A
B
Q
CC
E C
V
R R
CQ
I
CEQ
V
CC
V
CE
v
C
i
Le milieu de la droite de charge correspond au milieu du segment AB, le point de fonctionnement
étant au milieu, on en déduit :
et
2 2( )
2,5
52,08
2(1 0,2)
CC CC
CEQ CQ E C
CEQ
CQ
V V
V I R R
V V
I mA
Le courant est donc
C
I
égal à :
2,08
C
I mA
Le circuit de la figure 1 est équivalent à celui représenté ci-dessous :

4
T
V
T
R
E
R
CC
V
C
R
BE
V
B
I
1
1 2
1 1 2
1 2 1 2
0
T CC
T
E E BE C T
T
T C BE E C
C
CC BE E C
R
V V
R R
R
R I V I V
R
V I V R I
I
R R R
V V R I
R R R R
Posons :
1 2 11,25a R R k   
1 2
2 2
2
2 2
2 1
( )
( )
0,02 5,234 43,695 0
8,64 11,25 8,64 2,6
C
CC BE E C
C
CC BE E C
I
R V R a V R I
I
a R V R a V R I
R R
R k R k
2)
1
2
2,6
8,6
R k
R k
Lorsque le courant de saturation de la jonction BC est non nul, on peut écrire :
0
0
0 0
( 1)
C E CB
C B CE
CE CB
I I I
I I I
I I
0CB
I
est le courant de saturation de la jonction base collecteur, l’émetteur en circuit ouvert.

5
Maille d’entrée
0
0
( 1)
E E BE T B T
E C CB
R I V R I V
I I I
Soit :
0
0
( ) ( ) 0
C CE
E C CB BE T T
I I
R I I V R V
D’autre part :
00 CE CB
II
Donc :
0 0
0
( ) ( ) 0
( )
C
E C CB BE T CB T
T E T CB BE
CT
E
I
R I I V R I V
V R R I V
IR
R
A la température
1
T
:
1
1 0
0,7 , 5
BE CB
V V I A
A la température
2 1 , 20T T T T c     
2 1
2 . 0,04
0,7 0,04 0,66
BE
BE BE BE
V mV T V
V V V V
Le courant
0CB
I
double de valeur pour chaque augmentation de 10°c, on peut donc écrire :
2 1
0 0
0
4 20
20 5 15
CB CB
CB
I I A
I A A A
En termes de facteurs de stabilisation, la variation du courant s’écrit :
0
0
V
I
C C
C CB BE
CB BE
S
S
I I
I I V
I V
est considéré constant.