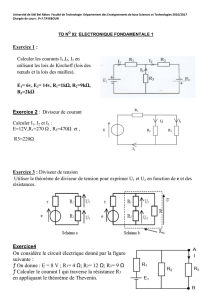
Autour de l`irrégularité des connexions méromorphes

THÈSE
Présentée pour obtenir
LE GRADE DE DOCTEUR EN SCIENCES
DE L’ECOLE POLYTECHNIQUE
Spécialité: Mathématiques
par
Jean-Baptiste Teyssier
Autour de l’irrégularité des connexions
méromorphes
Soutenue le 23 septembre 2013 devant la Commission d’examen:
M. Ahmed ABBES (Président du jury)
M. Yves ANDRÉ (Rapporteur)
M. Gaëtan CHENEVIER (Examinateur)
M. Michel GRANGER (Rapporteur)
M. Claude SABBAH (Directeur de thèse)
M. Takeshi SAITO (Rapporteur)

Thèse préparée au
Centre de Mathématiques Laurent Schwartz
UMR 7640
91 128 Palaiseau CEDEX

Résumé
Les deux premières parties de cette thèse s’inscrivent dans le contexte des analogies entre
l’irrégularité pour les connexions méromorphes et la ramification sauvage des faisceaux
-adiques. On y développe l’analogue pour les connexions méromorphes de la construc-
tion d’Abbes et Saito, tout d’abord dans le cas d’un trait suivant [3], puis en dimension
supérieure selon [4].
En première partie, on prouve une formule explicite reliant les invariants produits
par la construction d’Abbes et Saito appliquée à un module différentiel Maux parties
les plus polaires des formes différentielles intervenant dans la décomposition de Levelt-
Turrittin de M.
Dans la seconde, on généralise en dimension supérieure l’observation issue de la pre-
mière partie que sur un corps algébriquement clos, les modules produits par la construc-
tion d’Abbes et Saito sont des sommes finies de modules exponentiels associés à des
formes linéaires. C’est l’analogue de l’un des résultats fondamentaux de [4].
Dans la dernière partie de cette thèse, on montre que le lieu des points stables d’une
connexion méromorphe Mle long d’un diviseur lisse est un sous-ensemble de l’intersec-
tion des lieux où les faisceaux d’irrégularité de Met End(M)sont des systèmes locaux.
Enfin, on discute d’une stratégie d’attaque de l’inclusion réciproque, et on démontre à
l’aide d’un critère d’André pour les points stables que si elle est vraie en dimension 2,
alors elle est vraie en toute dimension.
Abstract
The first two parts of this thesis take place in the realm of analogies between the ir-
regularity phenomenon for meromorphic connections and wild ramification for -adic
sheaves. We develope the analogue for meromorphic connections of Abbes and Saito’s
construction, first in the case of a trait following [3], and then in higher dimension ac-
cording to [4].
In the first part, we prove an explicit formula relating the invariants produced by
Abbes and Saito’s construction applied to a differential module Mto the most polar
parts of the differential forms occuring in the Levelt-Turrittin decomposition of M.
In the second part, we generalize to higher dimension the observation coming from
the first part that on an algebraically closed field, the modules produced by Abbes and
Saito’s construction are finite sums of exponential modules associated to linear forms.
This is the analogue of one of the fundamental results of [4].
In the last part of this thesis, we prove that the stable point locus of a meromorphic
connection with poles along a smooth divisor is a subset of the intersection of the loci
where the irregularity sheaves of Mand End(M)are local systems. Finally, we discuss
a strategy to attack the converse inclusion, and we prove that if it is true in dimension
2, then it is true in any dimension. This relies on André’s criterion for stable points.

Remerciements
Mes remerciements vont tout d’abord à Claude Sabbah, pour avoir accepté d’en-
cadrer cette thèse et m’avoir inculqué avec générosité et patience tout ce que je sais
aujourd’hui des D-modules. Qu’il voit dans ce travail l’expression de ma gratitude.
Cette thèse doit aussi beaucoup aux travaux pionniers d’Ahmed Abbes et Takeshi
Saito. Je remercie notamment Ahmed Abbes pour des discussions très stimulantes ainsi
que pour l’intérêt porté au présent travail. Je remercie aussi Yves André, Takeshi Saito
et Michel Granger pour une lecture à la fois méticuleuse et bienveillante du manuscrit
de cette thèse, ainsi que Gaëtan Chenevier pour avoir accepté de faire partie de mon
jury.
De la convivialité du déjeuner de 11h45 à la qualité des échanges scientifiques, le
plaisir que j’ai eu à réaliser cette thèse tient aussi aux conditions de travail excellentes
offertes par le Centre De Mathématiques Laurent Schwartz. J’en remercie chaleureuse-
ment toute l’équipe.
Je remercie aussi vivement Hélène Esnault de me permettre aujourd’hui de pour-
suivre mon travail outre-Rhin dans des conditions tout aussi exceptionnelles.
Pour finir, j’aimerais remercier Alexei Grinbaum et Alexandre Martin, pour avoir été
spontanément présents dans tous les moments qui ont jalonné cette thèse. Des moments
de doute aux moments les plus jubilatoires. A vous deux merci.