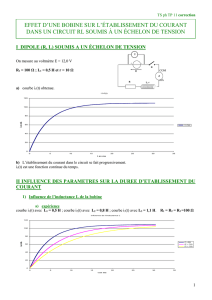
Les hacheurs à liaison directe

Les hacheurs à liaison directe
II. Hacheur parallèle (Boost)
1. Synthèse
•Dans le dispositif ci-contre :
K1 et K2 peuvent-ils être ouverts simultanément ? Non car la
source de courant serait en circuit ouvert ce qui engendrerait
une surtension à ses bornes (la source de tension serait aussi
court-circuitée mais cela ne pose pas de problème).
K1 et K2 peuvent-ils être fermés simultanément ? Non car la
source de tension serait court-circuitée (la source de courant
aussi mais cela ne pose pas de problème).
K
1
I
0
v
K1
(t)
i
K2
(t)
EU
v
K2
(t)
i
K1
(t)
K
2
Par la suite K1 est supposé fermé de 0 à aT et ouvert de aT à T.
•Que vaut vK2(t) lorsque K1 est fermé ? Que vaut vK1(t) lorsque K2 est fermé ?
D'après la loi des mailles : vK2(t) = - U lorsque K1 est fermé et vK1(t) = U lorsque K2 est fermé.
•Pour a = 0,5 : Représenter vK1(t), vK2(t), iK1(t) et iK2(t) en fonction du temps.
•Représenter iK1 = f(vK1) et iK2 = f(vK2). En déduire les types d'interrupteurs à utiliser.
K1 est un interrupteur unidirectionnel commandé à
l'ouverture et à la fermeture car les commutations se
font sans changement de quadrant.
K2 est une diode car les commutations se font avec
changement de quadrant.
Corrigés hacheurs parallèles Page 1 TS1 ET 2013-2014
U

2. Étude en conduction continue
La conduction est dite continue si le courant dans la charge ne s’annule jamais.
a. Tension aux bornes de la charge
Dans le montage représenté ci-contre, l’interrupteur
unidirectionnel commandé à l’ouverture et à la fermeture
(ICOF) K et la diode D sont supposés parfaits.
Pendant une période de fonctionnement, l’interrupteur K est
fermé de 0 à aT et ouvert de aT à T.
•Quel est l’état de la diode entre 0 et aT, entre aT et T ?
K
I
0
u(t)
i
c
(t)
EU
D
Entre 0 et aT, l'interrupteur K est fermé la diode D est donc bloquée (équivalente à un interrupteur ouvert).
Entre aT et T, l'interrupteur K est ouvert la diode D est donc passante (équivalente à un interrupteur fermé).
•Représenter les évolutions de ic(t) et u(t) sur deux périodes.
•Exprimer la valeur moyenne de u(t) en fonction du rapport cyclique et de U. Justifier le nom de « hacheur
élévateur » parfois donné à ce montage.
La valeur moyenne est donnée par
u=1
T(T−α T)U
soit
u=(1−α)U
. La valeur moyenne de la
tension d'entrée u(t) est plus petite que la valeur moyenne de la tension de sortie U d'où le nom de hacheur
élévateur.
b. Intensité dans la charge
Dans le dispositif précédent, la source de courant est remplacée par une fém en série avec une inductance
(voir ci-dessous). Le courant i(t) n’est plus parfaitement lissé mais on suppose qu’il ne s’annule jamais.
L’interrupteur K et la diode sont supposés parfaits.
Pendant une période de fonctionnement, l’interrupteur K est fermé de 0 à aT et ouvert de aT à T.
Corrigés hacheurs parallèles Page 2 TS1 ET 2013-2014
U

➢Étude de 0 à aT
•Représenter le schéma équivalent du montage en
remplaçant K et D par un circuit ouvert ou fermé.
•Établir la relation entre E, L et
di(t)
dt
.
D'après la loi des mailles
E – L d i(t)
dt =0
Ku(t)
i
c
(t)
EU
D
i(t)
L
EEEEEEEEEEEEEEEEEEEEEEEEE
•À partir de la relation précédente, établir l’expression littérale de i(t). Pour t = 0, i(0) = Imin.
L'équation
E – L d i(t)
dt =0
est transformée en
d i(t)
dt =E L
. La dérivée du courant par rapport est une
constante (
E
L
) d'où la primitive
i(t)= E
Lt+B1
avec B1 une constante d'intégration.
Pour déterminer la constante d'intégration B1, on utilise la condition initiale « Pour t = 0, i(0) = Imin. ».
Pour t = 0 , l'équation
i(t)= E
Lt+B1
devient
i(0)= E
L0+B1
soit
i(0)=B1
. Puisque
i(0)=Imin
et
i(0)=B1
alors
B1=Imin
Finalement l'expression du courant est donnée par
i(t)= E
Lt+Imin
entre 0 et aT
➢Étude de aT à T
•Représenter le schéma équivalent du montage en remplaçant K et D par un circuit ouvert ou fermé.
•Établir la relation entre U, E, L et
di(t)
dt
.
D'après la loi des mailles
E – L d i(t)
dt – U=0
•À partir de la relation précédente, établir l’expression littérale de i(t). Pour t = aT, i(aT) = Imax.
Corrigés hacheurs parallèles Page 3 TS1 ET 2013-2014
U
uL(t)

L'équation
E – L d i(t)
dt – U=0
est transformée en
d i(t)
dt =E – U L
. La dérivée du courant par rapport
est une constante (
E – U
L
) d'où la primitive
i(t)= E – U
Lt+B2
avec B2 une constante d'intégration.
Pour déterminer la constante d'intégration B2, on utilise la condition initiale « Pour t = aT, i(aT) = Imax. ».
Pour t = aT , l'équation
i(t)= E – U
Lt+B2
devient
i(αT)= E – U
LαT+B2
soit
B2=i(αT)− E−U
LαT
. Puisque
i(αT)=Imax
alors
B2=Imax−E−U
LαT
Finalement l'expression du courant entre aT à T est donnée par
i(t)= E – U
Lt+Imax−E−U LαT
qui
peut aussi s'écrire
i(t)= E – U
L(t−α T)+Imax
➢Étude de l’ondulation
•Représenter l’allure de i(t) sur une période de fonctionnement en faisant apparaître Imax, Imin, aT et T.
Le courant augmente linéairement de Imin à Imax entre
0 et aT et diminue linéairement de Imax à Imin entre aT
et T.
•Exprimer l’ondulation Di de i(t) en fonction de U, E, L, a et T.
À l'instant t = T, le courant est minimal : i(T) = Imin ; l'équation
i(t)= E – U
L(t−α T)+Imax
permet
d'écrire
Imin=E – U
L(T−α T)+Imax
soit
Δi=Imax−Imin =E – U
L(T−α T)
•Représenter l’allure de u(t) sur une période et exprimer sa valeur moyenne en fonction de a et U.
D'après un résultat trouvé précédemment
u=(1−α)U
.
•Exploiter les deux résultats précédents pour trouver la relation
i=E
LT
.
D'après la loi des mailles,
E – uL(t)– u(t)=0
(
uL(t)
est la tension aux bornes de l'inductance, voir
le schéma précédent). Pour les valeurs moyennes, cette équation devient
E – uL– u=0
; comme le
courant i(t) est périodique alors la tension aux bornes de l'inductance a une valeur moyenne nulle d'où
E=u
soit
E=(1−α)U
.
En remplaçant U par
E
(1−α)
dans l'équation
Δi=E – U
L(T−αT)
on obtient
Δi=
E−E
1−α
L(T−α T)
soit
Δi=
(1−α)E−E
1−α
L(T−α T)=(1−α) E−E L(1−α) (1−α)T
et finalement
Corrigés hacheurs parallèles Page 4 TS1 ET 2013-2014

Δi=E
LT
Remarque : on obtient la même relation beaucoup simplement en utilisant l'équation
i(t)= E
Lt+Imin
à
l'instant t = aT.
•Comment évolue l’ondulation lorsque la fréquence augmente ? Lorsque l’inductance L augmente ?
Si la fréquence augmente alors la période diminue (
f=1
T
) et l'ondulation diminue. Si l'inductance L
augmente alors l'ondulation diminue.
c. Dimensionnement de l'interrupteur et de la diode
•Représenter les chronogrammes de la tension et l’intensité pour l’interrupteur K.
•Représenter les chronogrammes de la tension et l’intensité pour la diode D.
À gauche pour l'interrupteur K et à droite pour la diode :
•En déduire les valeurs maximales de la tension à leurs bornes ainsi que les valeurs moyenne et efficace des
intensités qui les traversent (pour ces calculs, le courant dans la charge est supposé parfaitement continu).
L'interrupteur K doit supporter une tension U en direct ; la diode D doit supporter une tension -U en inverse.
Valeurs moyennes en supposant Imin = Imax = I0 :
iK=1
TαT I0=α I0
et
iD=1
T(T−α T)I0=(1−α) I0
Valeurs efficaces en supposant Imin = Imax = I0 : on élève les signaux au carré puis on prend les valeurs
moyennes et enfin les racines carrées.
IKeff =
√
1
TαT I0
2=
√
αI0
et
IDeff =
√
1
T(T−α T)I0
2=
√
1−α I0
Corrigés hacheurs parallèles Page 5 TS1 ET 2013-2014