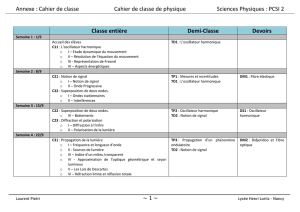
I. Relations d`incertitude.

INÉGALITÉS DE HEINSENBERG SPATIALES
I. Relations d’incertitude.
1. Incertitude statistique
Quand on observe la figure d’interférence produite photon par photon, on constate que les
maxima d’intensité correspondent aux zones où la probabilité de présence du photon est
maximum : la mécanique quantique est une théorie probabiliste.
Le caractère aléatoire de la détection fait que toute mesure si précise soit-elle s’accompagnera
toujours d’une incertitude de type statistique (on parle aussi d’indétermination quan-
tique).
Plaçons nous à une dimension. Si on mesure la valeur de x, en répétant Nfois la même mesure
sur Nparticules préparées dans le même état, on obtiendra une dispersion des mesures.
L’ensemble des mesures se distribue suivant la densité de probabilité |ψ(x, t)|2. La valeur
moyenne 1est
<x>=Z+∞
−∞
x|ψ(x, t)|2dx
Le carré de l’écart quadratique moyen, qui mesure la dispersion des mesures autour de la
valeur moyenne, est donné par
(∆x)2=<(x−<x>)2>=< x2>−<x>2
car
(∆x)2=< x2−2x < x > +<x>2>
=< x2>−2< x >2+<x>2
=< x2>−<x>2
On retiendra donc
∆x=√< x2>−<x>2
1. elle correspond à l’espérance mathématique vue en terminale
1

On peut définir de même l’incertitude statistique pour pxla composante suivant ~uxde la
quantité de mouvement.
∆px=p< p2
x>−< px>2
Remarque : Ces incertitudes n’ont rien à voir avec une quelconque imprécision des mesures.
Elles sont intrinsèquement quantiques.
Si la précision de mesure δx des appareils de mesure est supérieure à ∆xon a une bonne
représentation d’un objet ponctuel.
2. Relations d’incertitude
Revenons à l’expérience de diffraction (de
photons, d’électrons ou d’atomes...) par une
fente fine de largeur a. Plus la fente est fine,
plus la tache de diffraction est large. On note
θla demi-largeur angulaire de la tache cen-
trale de diffraction.
Si on se place au niveau de la fente diffractante, de largeur a, l’incertitude sur la position x
est de l’ordre de grandeur de la largeur de la fente :
∆x'a
La composante px=~p.~uxde la quantité de mouvement de la particule considérée varie de
−psin θàpsin θ(en considérant la largeur angulaire de la tache centrale où se concentre la
majorité des particules diffractées). Or, sin θ'λ
a, avec λla longueur d’onde de de Broglie.
L’ordre de grandeur de l’incertitude sur la mesure de pxest donc de l’ordre de
∆px'psin θ
Or, sin θ'λ
a, avec λla longueur d’onde de de Broglie. On en déduit
∆px'pλ
a
d’après la relation de de Broglie p=h
λ, d’où
∆px',h
λ
λ
a'h a
On a donc
a∆px'h
∆x∆px'h
2

On a raisonné ici sur des ordres de grandeurs. De manière générale, la relation d’incertitude
de Heisenberg, s’écrit sous la forme :
∆x∆px>
~
2avec ~=h 2π.
Cette relation s’applique bien sûr aux deux autres autres directions de l’espace :
∆y∆py>
~
2∆z∆pz>
~
2
Par contre ∆xi∆pj, n’admet pas de limite inférieure non nulle pour i6=j.
On ne peut donc pas mesurer simultanément la position et la quantité de mouvement (donc
la vitesse) avec une précision arbitrairement grande. La notion classique de trajectoire, pour
laquelle la position et la vitesse sont déterminées à chaque instant disparaît.
Si on confine des particules, leurs vitesses seront très dispersées.
Inversement, si on prépare des particules de manière à ce que leur vitesse soit bien déterminée,
alors l’indétermination sur leur localisation sera grande (les particules seront délocalisées).
Remarque : on comprend ici tout l’intérêt d’obtenir un faisceau de particules très monociné-
tique lorsqu’on réalise une figure d’interférence avec des particules. La vitesse des particules
étant très bien définie, ∆vxest faible, donc ∆pxégalement ce qui entraîne une extension spa-
tiale ∆ximportante : elle doit bien sûr être supérieure à l’écart entre les deux fentes si on
souhaite observer des interférences !
II. Énergie minimale de l’oscillateur harmonique quan-
tique
1. Oscillateur harmonique classique (rappels)
On a étudié en début d’année le mouvement har-
monique.
Si on note xl’écart par rapport à la position d’équi-
libre, le mouvement harmonique est caractérisé par
x(t) = Acos(ω0t+ϕ)
v(t) = −Aω0sin(ω0t+ϕ)
– la position xest comprise entre −Aet A
– la vitesse vest comprise −ω0Aet ω0A
L’énergie de l’oscillateur harmonique (correspondant à son énergie mécanique) est donnée par
E=Ec+Ep=1
2mv2+1 2kx2=1 2mv2+1 2mω2
0x2
On a montré que E=1
2kA2=1 2mω2
0A2avec ω0=rk
mpulsation propre de l’oscillateur.
3

Le modèle de l’oscillateur harmonique a de nombreuses applications :
– en général, le mouvement conservatif d’un point au voisinage d’une position d’équilibre
stable est du type harmonique
– au niveau microscopique, les forces d’interactions entre les atomes d’une molécule sont
modélisées par des forces élastiques. On peut donc se ramener au modèle de l’oscillateur har-
monique pour étudier les vibrations de molécules.
Classiquement, quelle peut-être la valeur minimale de l’énergie ?
la réponse est Emin = 0
Dans ce cas la particule est en O, avec une vitesse nulle : elle est au repos au niveau de la
position d’équilibre. Sa position et sa vitesse sont donc parfaitement définies. On aura donc
∆x= 0 et ∆px= 0.
Ce résultat est en total désaccord avec l’inégalité de Heisenberg ∆x∆px>~/2.
L’énergie minimale de l’oscillateur harmonique quantique ne peut pas être nulle.
2. Oscillateur harmonique quantique
L’étude quantitative des vibrations de molécules nécessite un traitement quantique. Il faut,
pour trouver les niveaux d’énergie de l’oscillateur, résoudre l’équation de Schrödinger. Cette
résolution dépassant largement le cadre du programme, on se contentera d’un raisonnement
semi-classique.
L’inégalité d’Heisenberg va nous permettre permet d’évaluer l’ordre de grandeur de l’énergie
minimale d’un oscillateur harmonique quantique.
Pour une énergie donnée, le mouvement est borné. On peut alors évaluer les ordre de grandeurs
des incertitudes ∆xet ∆px.
Classiquement : E=1
2mv2+1 2kx2=p2 2m+1 2mω2
0x2=1
2mω2
0A2
<x>= 0,< px>= 0 ;
< x2>=1
2A2=E mω2
0
;
< p2
x>=m2< v2 x>=m2A2ω2 0<sin2(ω0t+ϕ)>=m2A2ω2
0
2=mE
On en déduit les incertitudes sur xet p:
∆x=√< x2>−< x >2=√< x2>=sE
mω2
0
∆px=p< p2
x>−< px>2=p< p2 x>=√mE
∆x∆px>
~
2
sE
mω2
0
√
mE >
~
2
E>
~ω0
2
4

Notre calcul, très grossier, ne permet en toute rigueur que d’obtenir un ordre de grandeur de
l’énergie minimale.
Cependant, en résolvant l’équation de Schrödinger on trouve que les niveaux d’énergie de
l’oscillateur sont quantifiés. Les valeurs des énergies des différents niveaux s’expriment sous
la forme :
En=n+1
2~ω0avec n∈N
On constate que le niveau d’énergie minimale (pour n= 0) vaut bien Emin =1
2~ω0.
Remarque : l’hypothèse de Planck était donc bien fondée : quand un oscillateur passe d’un
niveau n+ 1 au niveau nil émet un photon d’énergie En+1 −En=~ω0=hν et il l’absorbe
pour passer du niveau nau niveau n+ 1.
Nous allons voir dans l’exemple suivant que, de manière générale, un mouvement limité spa-
tialement (état lié) entraîne une quantification des niveaux d’énergie.
III. Particule confinée
1. Puits de potentiel infini classique
On considère une particule contrainte à être
confinée dans un certain domaine spatial de
largeur L.
Un puits de potentiel infini de largeur Lper-
met de décrire cette situation.
Ep(x) = 
∞si x < 0
0si 0< x < L
∞si x>L
À énergie totale constante, la particule possède deux vitesses possibles telles que E=1
2mv2
x.
On peut imaginer un mouvement de va et vient entre les deux parois x= 0 et x=L, le
corpuscule étant contraint de "rebondir" sur chacune des parois limites.
Classiquement, l’énergie minimale possible est bien sûr nulle (particule au repos dans l’inter-
valle [0, L]). Mais, comme on l’a vu dans le chapitre précédent, cet état n’est pas compatible
avec l’inégalité de Heisenberg : la limitation spatiale du mouvement entraîne une énergie
minimale non nulle.
2. Quantification des niveaux d’énergie
Le confinement entre 0et L, le comportement ondulatoire des particules, ainsi que l’additivité
des fonctions d’ondes, permet de chercher des solutions sous la forme d’une superposition
d’ondes planes progressives se propageant dans deux directions opposées de manière à former
une onde stationnaire.
5