Vagues-hydrodynamique. Cours 1.

Vagues-hydrodynamique. Cours 1.
Outre le site du shom (http://www.shom.fr/fr page/fr act oceano/vagues/vagues f.htm),
(voir aussi les liens: http://www.shom.fr/fr page/fr act oceano/vagues/PLUS/LIENS/index.html)
1 Supports p´edagogiques sur le web
Pour la cin´ematique des vagues: Les applets java de Robert Dalrymple, en par-
ticulier celles intitul´ees ‘linear wave kinematics’ et ‘superposition of waves’, les
autres seront plus claires apr`es les prochains chapitres (http://www.coastal.udel.edu/faculty/rad/)
Dans le mˆeme genre, il y a aussi une animation sympathique dans les cours
de l’Universit´e de San Francisco (SFSU),
(http://funnel.sfsu.edu/courses/gm309/exercises/preclass.5.wavesbeaches )
Enfin, dans une s´erie des cours destin´es aux pr´evisionnistes, le UCAR propose
quelques cours assez bien faits (en anglais), sur le site
http://meted.ucar.edu/topics Marine.php
Les sujets les plus en rapport avec le chapitre 1 sont:
•Wave types and characteristics
•Wave life cycle II: propagation and dispersion.
Enfin, en allant bien au del`a du chapitre 1, une extension sur les statistiques
`a long terme peut se trouver dans le cours de Harald Krogstad et Øivind
Arntsen,
http://folk.ntnu.no/oivarn/hercules ntnu/LWRcourse (voir la partie B, ”ir-
regular waves”).
1

2 Exercices
2.1 Distrbution des hauteurs de vagues
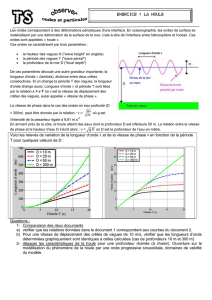
Sur la figure 1.2 (page 5) un peut compter environ 26 vagues. Quelle est
la p´eriode moyenne d’une vague? Quelle est (`a peu pr`es) la hauteur signi-
ficative? Quelle est la hauteur maximale? En admettant que les conditions
m´et´eorologiques restent constantes, et en faisant l’hypoth`ese d’un spectre
´etroit et d’une ´el´evation de la surface Gaussienne, quelle est la probabilit´e
d’avoir une vague de 12 m de haut? Connaissant la p´eriode moyenne que
l’on a calcul´ee, combien de temps faudrait-il attendre pour observer une telle
vague?
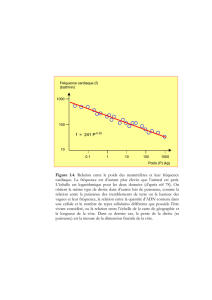
La figure 1.4 (page 7), montre un enregistrement similaire, mais pour les com-
posantes uet vde la vitesse au fond. Que peut on dire de la distribution du
module de la vitesse? Comment d´efinir une valeur significative des amplitudes
de fluctuation de vitesse?
2.2 Propri´et´es des vagues lin´eaires
Soit une houle r´eguli`ere de p´eriode T= 10 s et d’amplitude a= 1 m. Cette
houle se propage par 300 m de fond. Quelle en est le nombre d’onde k? La
vitesse de phase C, et la vitesse de groupe Cg? Quelle est l’amplitude des
vitesses en surface et au fond? Quel est le flux d’´energie par unit´e de longueur
de crˆete? La d´erive de Stokes en surface? Le flux de masse? (transport induit
par la d´erive de Stokes)
Cette houle se propage ensuite vers des petits fonds, et atteint 30 m de pro-
fondeur de telle sorte que le flux d’´energie est identique. Quelles sont les nou-
velles amplitudes des ´el´evations, des vitesses de surface et de fond?
Enfin, la houle arrive par 10 m de fond, dans les mˆemes conditions. Qu’en
est-il?
2.3 Exemple d’extension de la th´eorie d’Airy: ondes de gravit´e-capillarit´e et
ondes capillaires
Cet exercice est peut ˆetre un peu plus difficile, mais il s’agit surtout de bien
comprendre comment on obtient la th´eorie d’Airy.
2

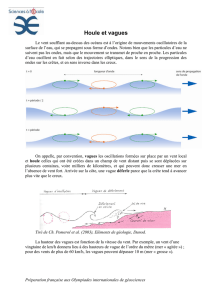
On consid`ere des vagues r´eguli`eres se propageant sur un fond plat dans la
direction (Ox), comme pour la th´eorie d’Airy. Toutefois, on veut prendre en
compte la tension de la surface γqui correspond `a une ´energie de la surface
T=γρw= 0.074 J/m2. Cette tension de surface cr´ee une surpression dans
l’eau qui s’´ecrit dans ce cas, pw=pa−T ∂ζ/∂x2(N.B.: la pression est n´egative
sous les creux des vagues, ce qui a tendance `a y aspirer l’eau et donc faire
ensuite apparaˆıtre une crˆete.
On cherche des ondes se propageant comme les ondes d’Airy. La tension de
surface ne modifie que la condition dynamique en surface. Quelle est donc la
diff´erence entre les ondes d’Airy et les ondes capillaires que l’on va trouver?
Quels sont les points communs?
Quelle est la nouvelle relation de dispersion? Quelle est la vitesse de phase
Cet la longueur d’onde des ondes pour lesquelles Cest minimum? Quelle
est l’´energie des ces vagues? (ne pas oublier l’´energie de la surface qui est
proportionnelle `a la surface !)
2.4 Exemple d’extension de la th´eorie d’Airy: effet de la rotation de la terre
et ondes d’inertie gravit´e
Si on rajoute maintenant la force de Coriolis, que se passe-t-il? En partant
d’ondes d’Airy se propageant suivant (Ox), calculez la perturbation de vitesse
transversale v. Comparez la d´eriv´ee verticale de la moyenne du produit uv
avec la d´erive de Stokes. Que peut-on d´eduire de l’´equilibre moyen entre la
force de Coriolis induite par le transport de masse li´e aux vagues et un courant
moyen b u(z) uniforme sur l’horizontale, et la divergence du tenseur de Reynolds
∂huvi/∂z?
3