Thème : Observer - Ondes et matières – Ondes et particules Type de

Thème : Observer - Ondes et matières – Ondes et particules
Type de ressources : documentaires
Notions et contenus : « Les ondes dans la matière Houle, … »
Compétences travaillées :
- extraire l’information
- exploiter l’information (graphique ; relation)
Nature de l’activité : analyser et exploiter des informations
Résumé :
Deux documents sur les ondes de surface en mer, provenant de sites Internet, sont fournis à l’élève.
Ce dernier doit montrer par un raisonnement comprenant une exploitation de relations et de
graphiques, que les deux documents proposent des données concordantes.
Mots clefs : houle ; ondes ; longueur onde ; période
Académie où a été produite la ressource : TOULOUSE

Les données sur les ondes de surface en mer sont tirées des deux sites :
Document 1 : http://www.ifremer.fr/lpo/cours/vagues_ondes/shorthoule.html
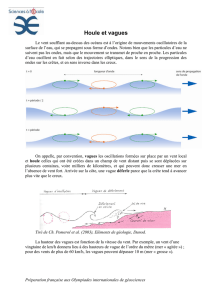
Les ondes correspondent à des déformations périodiques d'une interface. En
océanographie, les ondes de surface se matérialisent par une déformation de la surface de
la mer, c'est-à-dire de l'interface entre l'atmosphère et l'océan. Ces ondes sont appelées
« houle ».
Ces ondes se caractérisent par trois paramètres :
 la hauteur des vagues H ("wave height" en anglais)
 la période des vagues T ("wave period")
 la profondeur de la mer D ("local depth")
De ces paramètres découle une autre grandeur importante, la longueur d'onde  (lambda),
distance entre deux crêtes consécutives. Si on change la période T des vagues, la longueur
d'onde change aussi. Longueur d’onde  et période T sont liées par la relation  = v T où v
est la vitesse de déplacement des crêtes des vagues, aussi appelée « vitesse de phase ».
La vitesse de phase dans le cas des ondes en eau profonde (D > 300m) peut être donnée
par la relation : v où g est l’intensité de la pesanteur égale à 9,81 m.s-2
En arrivant près de la côte, la houle atteint des eaux dont la profondeur D est inférieure 50
m. La relation entre la vitesse de phase et la hauteur d’eau D s’écrit alors : v = où D
est la profondeur de l’eau en mètre.

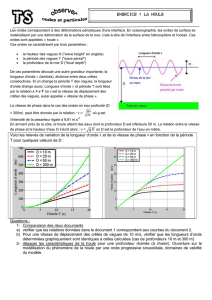
Document 2 : http://www.shom.fr/fr_page/fr_act_oceano/vagues/vagues.htm
Voici les relevés de variation de la longueur d’onde  et de la vitesse de phasev en fonction
de la période T pour quelques valeurs de D :
Pistes d’activité :
1- Comparaison des deux documents
a) Raisonnement complexe : vérifier que les relations données dans le document 1
correspondent aux courbes du document 2.
b) Raisonnement plus détaillé : Pour une vitesse de déplacement des crêtes de vagues
de 10 m/s, vérifier que les longueurs d’onde déterminées graphiquement sont
identiques à celles calculées (cas de profondeurs 10 m et 300 m)
2- Autre piste : à partir des deux documents, dégager les caractéristiques de la houle
pour une profondeur donnée (à choisir). Ouverture sur la modélisation du phénomène
de la houle par une onde progressive sinusoïdale, domaines de validité du modèle.
Éléments de correction :
1- Comparaison des deux documents
a) Raisonnement complexe : vérifier que les relations données dans le document 1
correspondent aux courbes du document 2.
Si D > 300 m :
Les deux relations et  = v T donnent v =

Comme le facteur est constant le graphe représentant v en fonction de T est une
droite passant par l’origine. Ce qui est vérifié sur le graphe de droite.
La relation donnant  en fonction de T :  = v T devient  = T2. Le graphe
représentant  en fonction de T est une parabole. Vérifier sur une valeur de T que le
graphe (T) donne une valeur correcte de . Ex : T = 15 s donne  = 350m.
Les deux graphes correspondent bien aux relations données dans le document 1
pour D > 300 m. 
Si D < 50 m :
Alors : v =
D’après cette relation, si la profondeur reste constante, alors la vitesse de phase doit
rester aussi constante.
Le graphe v(T) montre que cette relation est vérifiée si la période T est supérieure à
15 s pour D = 10 m et 20 m. La relation n’est vraie que pour de grandes périodes.
La relation donnant  en fonction de T :  = v T devient  = T.  soit être
proportionnelle à T. Or sur le graphe (T) ceci n’est vérifié que pour des périodes
supérieures à 15 s.
Le modèle possède donc des limites.
b) Raisonnement plus détaillé : Pour une vitesse de déplacement des crêtes de vagues
de 10 m/s, vérifier que les longueurs d’onde déterminées graphiquement sont
identiques à celles calculées (cas de profondeurs 10 m et 300 m)
Pour v = 10 m/s, à D = 10 m :
Choisissons T = 15 s
 = v T = T donne  = x 15 = 150 m ce qui est vérifié sur le graphe
(T).
Pour v = 10 m/s, à D = 300 m :
On lit T = 6 s et  = v T donne  = 10 x 6 = 60 m ce qui est vérifié sur le graphe (T).
2. Autre piste : à partir des deux documents, dégager les caractéristiques de la houle
pour une profondeur donnée (à choisir). Ouverture sur la modélisation du phénomène
de la houle par une onde progressive sinusoïdale, domaines de validité du modèle.

Pour D = 300 m, définir la forme et les grandeurs caractéristiques de l’onde associée
à la houle : sinusoïdale caractérisée par une période T, une vitesse de propagation
(ou vitesse de phase) v et une longueur d’onde .
Exemple de valeurs numériques : v = 20 m/s ; T = 13 s et  = 250 m.