énoncé

Spé y 2006-2007 page 1/3 Devoir n°1
Spé y 2006-2007 Devoir n°1
MÉCANIQUE DU POINT ; ÉLECTROCINÉTIQUE
EXERCICE I
Partie A
ÉTUDE DANS LE REFERENTIEL R DU LABORATOIRE :
Le mouvement est étudié dans le référentiel du laboratoire assimilé à un référentiel
galiléen et associé à un repère (O,
r
e
X,
r
e
Y,
r
e
Z).
Un palet
M
de masse
m
peut se mou-
voir sans frottement dans le plan
(,,)
Oxy
horizontal (table à coussin d’air par
exemple). Le champ de pesanteur est suivant la
verticale Oz :
r
g
= –g
r
e
Z (avec g > 0).
Le palet M est accroché à l’extrémité
d’un ressort (point
M
) de longueur à vide ℓ0, de
raideur k, dont l’autre extrémité est fixée en O.
La position de
M
est repérée dans la base
(O,
r
e
X,
r
e
Y) par OM x t e y t e
¾ ®¾
= +( ) ( )
r r
X
Y
ou dans la
base (
r
e
r,
r
e
q) par OM r t e M
¾ ®¾
=( ) ( )
r
r
.
I-A-1) Faire un bilan des forces. Montrer
qu’il y a conservation du moment cinétique,
r
L
0
par rapport à O.
I-A-2) À t = 0, le palet est lâchée, sans vitesse initiale, d’une longueur 1,2.ℓ0 :
OM t e
¾ ®¾
= =( ) , .0 1 2
0
lr
X
.
a) Calculer
r
L
0
. Quelle est la nature de la trajectoire ?
b) Déterminer l’évolution temporelle de la longueur du ressort, ℓ(t) = OM(t). Préciser
l’intervalle de variation de ℓ, longueur du ressort.
I-A-3) On lance la particule d’un point OM OM t e
¾ ®¾ ¾ ®¾
= = =
0
1
0( ) lr
X
, avec une vitesse initiale
r
v
0 = ℓ1w
r
e
Y , orthogonale à
OM
¾ ®¾
0
. Dans la suite, on travaillera en coordonnées polaires dans le plan
(O, x, y).
a) Préciser
r
L
0
en fonction r(t) et
d
t
dt
q
(
)
puis en fonction des conditions initiales et des
vecteurs de base. On notera
L
le module de
r
L
0
.
b) Rappeler l’expression de l’énergie potentielle élastique. Doit-on tenir compte de
l’énergie potentielle de pesanteur pour étudier le mouvement ? Montrer qu’il y a conservation de
l’énergie mécanique EM. Préciser l’expression de EM en fonction des conditions initiales, en fonc-
tion de r(t),
dr
t
dt
(
)
,
d
t
dt
q
(
)
, m, k et ℓ0.
c) Montrer que l’énergie mécanique peut s’écrire : E m dr t
dt E r
M EFF
=
F
H
G
I
K
J+
1
2
2
( ) ( ). Pré-
ciser l’expression de EEFF(r). Tracer l’allure de EEFF(r).
d) Le palet peut-elle s’éloigner indéfiniment du pôle d’attraction ?
e) La vitesse de la particule peut-elle s’annuler au cours de son mouvement ?
M
q
x
y
k, ℓ0
r
e
X
r
e
Y
r
e
r(M)
r
e
q(M)
r
e
Z ¤

Spé y 2006-2007 page 2/3 Devoir n°1
f) La particule peut-elle passer par le centre d’attraction au cours de son mouve-
ment ?
I-A-4) On cherche à déterminer une condition entre ℓ1 et w pour avoir un mouvement circu-
laire.
a) Montrer que dans ce cas, le mouvement est uniforme.
b) Déterminer ℓ1 en fonction de k, ℓ0 et w. Est-elle valable pour tout w ?
Partie B
ÉTUDE DANS UN REFERENTIEL R’ EN ROTATION UNIFORME AUTOUR D’UN AXE FIXE :
Le mouvement est étudié dans le référentiel R’ en rotation uniforme autour d’un axe Oz fixe,
de vecteur vitesse
r
r
w
w
=
e
Z
et associé au repère (O,
r
e
r,
r
e
q,
r
e
Z).
On considère une particule M de
masse
m
pouvant se mouvoir sans frotte-
ment le long de l’axe (O,
r
e
r). Le champ de
pesanteur est toujours suivant la verticale
Oz :
r
g
= –g
r
e
Z.
La masse
m
est accrochée à
l’extrémité d’un ressort (point
M
) de lon-
gueur à vide ℓ0, de raideur k, dont l’autre
extrémité est fixée en O. La position de
M
est repérée dans la base (O,
r
e
r,
r
e
q) par
OM re M
¾ ®¾
=r
r
( ).
I-B-1) Préciser les expressions vecto-
rielles des forces d’inertie dans la base
(O,
r
e
r,
r
e
q,
r
e
Z).
I-B-2) Montrer que la force d’inertie d’entraînement dérive d’une énergie potentielle EP,ENT
que l’on précisera.
I-B-3) En est-il de même pour la force d’inertie de Coriolis ou complémentaire ?
I-B-4) Déterminer l’énergie potentielle totale. Tracer l’allure de EP(r). On distinguera les 3
cas possibles selon la valeur de w.
I-B-5) Déterminer la longueur ℓ2 correspondant à la position d’équilibre dans le référentiel
R’. À quelle condition sur w le résultat est-il possible ? Cet équilibre est-il stable ? Quel est alors le
mouvement dans le référentiel du laboratoire ?
I-B-6) Comparer ℓ2 à ℓ1 du paragraphe précédent. Conclusion.
EXERCICE II
Partie A
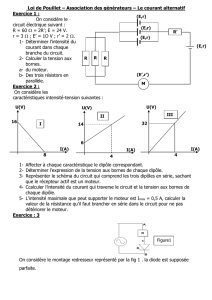
On considère un amplificateur à transistor dont le schéma équivalent en régime sinusoïdal de
faible amplitude est le circuit représenté sur le schéma de la figure ci-contre. La source qui délivre
la tension d'entrée vE(t) = VEcos(wt) est un générateur de
tension autonome parfait délivrant une tension sinusoïdale de
valeur efficace VE et de pulsation w. Les deux autres générateurs,
parfaits eux aussi, sont des sources liées, commandées respecti-
vement, pour la source de tension, par la tension de sortie
vS(t) = VA – VB et, pour la source de courant, par le courant
i(t) =I0cos(wt) délivré par la source autonome (I0 déoend de V0 et du reste du circuit). Les quantités a et
b sont des constantes.
Du point de vue de ses bornes de sortie A et B, ce réseau dans lequel est compris le résistor
de résistance R connecté entre les bornes A et B, est équivalent à un générateur qui, dans la représenta-
M
w
t
x
y
k,
ℓ
0
r
e
X
r
e
Y
r
e
r(M)
r
e
q(M)
r
e
Z ¤
r
R
0
R
vE(t)
i(t)
b
i(t)
vS(t)
a
vS(t)
–Ÿ A
–Ÿ B

Spé y 2006-2007 page 3/3 Devoir n°1
tion de Thévenin, est constitué par une source de tension de force électromotrice eTH(t) associée en série à
un résistor de résistance RTH.
Dans la représentation de Norton, ce générateur est constitué d'une source de courant, de courant
électromoteur IN(t) associée en parallèle à un résistor de résistance RN.
II-A-1) Exprimer la résistance d'entrée RE du circuit définie par le rapport : R
v
t
i t
E
E
=
(
)
( ) .
II-A-2-a) Calculer eTH(t) en fonction de vE(t) et des paramètres constants du circuit.
b) Calculer IN(t) en fonction de vE(t) et des paramètres constants du circuit.
c) Calculer RTH.
d) Calculer RN.
II-A-3-a) Un résistor de résistance RU est connecté entre les bornes A et B, en parallèle sur le
résistor de résistance R. Exprimer en fonction de RU et des caractéristiques du générateur équivalent, la puis-
sance moyenne, calculée sur une période et notée PU, dissipée dans RU.
b) Pour quelle valeur RU0 cette puissance est-elle maximale ?
Partie B
Un dipôle comporte entre ses bornes un résistor de
résistance R et un condensateur de capacité C placés en
série. On le place aux bornes de l’amplificateur étudié ci-
dessus, décrit par le modèle de Thévenin avec une force
électromotrice eTH supposée constante et une résistance
interne RTH en série avec un interrupteur
K
.
Initialement, le circuit est ouvert et le condensa-
teur déchargé. On note uC(t) la tension aux bornes du
condensateur.À l’instant t = 0, on ferme l’interrupteur K.
II-B-1) Déterminer sans calcul et en le justifiant uC(0+) et i(0+).
II-B-2-a) Établir l’équation différentielle à laquelle obéit uC(t).
b) Déterminer la constante de temps t du circuit et donner son interprétation physi-
que.
c) Établir l’expression de uC(t).
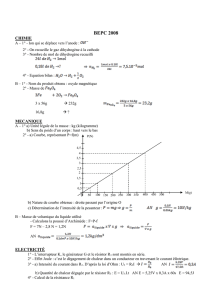
II-B-3) Dans l’étude expérimentale
du circuit RC, on observe l’oscillogramme
ci-contre en utilisant un générateur déli-
vrant des signaux créneaux.
Les sensibilités sont : 1V/carreau
vertical ; 0,1 ms/carreau horizontal .
On néglige les caractéristiques de
l’oscilloscope.
a) Identifier les courbes (1)
et (2) aux voies A et B en justifiant votre
choix.
b) Doit-on être sur le cou-
plage alternatif AC ou le couplage continu
DC ?
c) Préciser l’expression de la
tension au point P. Sachant que R = 100 W, déterminer RTH.
d) En déduire la valeur de C et eTH.
e) Estimer une majoration de la fréquence du signal carré utilisé.
f) Comment pourrait-on observer l’intensité ?
R
TH
R
Voie A Voie B
i
uC(
t
eTH
K
GENERATEUR