Physique - 2006 - Tronc Commun - Semestre 2

DÉPARTEMENT DU PREMIER CYCLE
–––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––––
DEVOIR DE SYNTHÈSE DE PHYSIQUE
14 Juin 2006 Durée :
3 heures (09h -12h)
Tout document est interdit. Toute calculatrice d’un modèle autre que celui autorisé, est interdite. Les élèves sont priés :
- d'indiquer leur nom et groupe, le nombre d’intercalaires, soigneusement numérotées,
- d’écrire très lisiblement, de soigner la rédaction, l’orthographe et la présentation matérielle ;
- d'indiquer ou d'énoncer les lois ou principes utilisés, de justifier les résultats par des explications (claires, précises,
concises) indispensables à une bonne compréhension de la solution proposée ;
- de mettre en évidence les résultats littéraux ou numériques (les principaux étant encadrés en couleur autre que rouge).
BAREME APPROXIMATIF sur 40: I :10 pts ; II :14 pts ; III : 15 pts ; tenue copies :1 pt
Problème I : Balance électrostatique
Les deux armatures d'un condensateur sont deux disques métalliques (A)
et (B) de surface S et de masse Ma, d'axe commun z'Oz dont un vecteur
unitaire ascendant est uz. La distance entre (A) et (B) est z. Les potentiels
de (A) et (B) sont VA et VB. (A) est placé sur un support isolant et fixe. (B)
est suspendu par deux ressorts parfaitement isolants et peut se déplacer
suivant l'axe z (figure 1). On suppose les armatures infinies dans des
directions perpendiculaires à z. Le champ de pesanteur est
z
g gu=-
.
Figure I.1
L'espace entre les armatures est vide. Lorsque les potentiels VA et VB
sont nuls, le système est en équilibre lorsque (B) porte une masse M, la
distance entre les armatures est alors z=e.
Si on porte (A) au potentiel U positif en maintenant VB=0, soit U=VA-VB, il
faut remplacer la masse M par M-m pour obtenir la même distance z=e
entre les armatures. On obtient l'état d'équilibre (I).
1
z
e
U
M
M-m
(A)
(B)
(A)
(B)
O
u
z

1) Questions préliminaires :
a) Faire le bilan des forces qui s’appliquent uniquement sur le plateau
(B) lorsque U = 0,
b) Lorsque U est positif, donner l’origine et le sens de la force
électrostatique qui s'ajoute sur (B)
2) En analysant l'équilibre mécanique (I), montrer alors que la force
électrostatique subie par (B) a pour expression:
z
F mgu=-
On pourra noter Fressort la force exercée par les ressorts sans qu'il soit
nécessaire de connaître son expression exacte.
3) Dans la suite les données sont à prendre parmi U, S, e, ε0 et
z
u
.
a)En utilisant l'expression de la capacité d'un condensateur plan, calculer
la densité surfacique de charge σB portée par l'armature (B).
b)En déduire une nouvelle expression de la force électrostatique
F
subie
par (B).
4) Exprimer U en fonction de S, e, m, g et ε0 et calculer numériquement
U pour m=8,1g, e=1 cm, S=900 cm2, g=9,81ms-2 et ε0=1/36π109 USI. On
suppose ∆m=0,1g et ∆e=0,01 cm. Calculer l'incertitude sur U, ∆U.
5) (A) étant maintenu au potentiel VA=U et (B) à VB=0, on remplace la
masse m par une masse m'. La distance entre les armatures devient alors
z=e' telle que e'>e. On obtient l'état d'équilibre (II). Les données sont à
prendre parmi U, S, e, e' et ε0.
a) Calculer l'énergie WG fournie par la source de tension lors de cette
transformation.
b) La transformation est supposée réversible. Exprimer le travail
mécanique reçu par le système à l'aide d'un bilan énergétique.
Problème II: Conduction et électrocinétique : Modélisation d’une
fibre nerveuse ( Les parties A et B sont indépendantes)
Dans le système nerveux animal, les signaux transportant l’information
résultent d’impulsions de nature électrique. Ces impulsions, sont
transportées par des fibres nerveuses appelées axones. L’axone est une
membrane cylindrique de rayon r de l’ordre de 10−6 m et d’épaisseur de
l’ordre de 10−9 m. Sa longueur ℓ peut dépasser le mètre. L’axone contient
un liquide ionique conducteur,
et l’axone est alors polarisée comme sur la figure II.1
2

Fig. II.1 – Axone polarisée
Fig. II.2 – Modèle d’un élément de longueur
∆ x d’axone
Quand une perturbation électrique V0 est appliquée à l’axone, il apparaît
un courant d’axone ia dans le liquide. Beaucoup de propriétés de la fibre
nerveuse peuvent être interprétées en considérant l’axone comme un
mauvais conducteur de résistivité non nulle et présentant un courant de
fuite i f à travers sa membrane . Un petit segment d’axone (ab,cd), de
longueur ∆x, est ainsi schématisé électriquement par la figure II .2 :
– R1 est la résistance du segment considéré (de résistivité constante ρ a)
de l’axone (membrane + liquide) qui s’oppose au courant longitudinal ;
– R2 est la résistance de fuite de la membrane du segment considéré de
l’axone ;
- C est la capacité de cette même membrane.
A. Etude des caractéristiques d’un modèle de segment d’axone
de longueur ∆x
1) Soit Cm, la capacité par unité de surface de la membrane et Gm la
conductance de fuite par unité de surface de l’axone, montrer que :
12 a
x
Rr rp
D
=
;
2
1
2
m
RG r xp =� �D
;
2
m
C C r xp= � �D
(pour la détermination de C, on pourra identifier la paroi, en raison de sa
très faible épaisseur, a un condensateur plan).
2) Déterminer les valeurs numériques correspondantes R1, R2 et C pour
un segment de longueur ∆x = 1 cm de l’axone. Les données numériques
sont : ρ
a=1 Ω m ; Cm= 10-2 F.m-2 ; Gm=5 S.m-2 ; r = 3 10 -6 m.
3 ) On applique entre a et b (l’entrée de l’axone) une tension V0.
En négligeant le courant qui sort du segment d’axone en d (voir figure
II.2) et en considérant le courant ic qui traverse le condensateur lors de
l’application de la tension V0, déterminer l’équation différentielle
permettant de déterminer le potentiel V aux bornes de la capacité C.
B. Modèle simplifie d’axone
4) On considère le réseau infini de la figure II.3 et on désigne par RT la
résistance totale de ce réseau (entre les points a et b ).
Figure II 3 – Réseau résistif infini
3

En considérant que la résistance totale de la partie du circuit à droite
des points d et e est aussi RT, démontrer que l’expression de la résistance
totale RT est :
2
1 1 2
1 ( 4 )
2
T
R R RR
R+ + =
.
5) Démontrer que, si la tension appliquée à l’entrée du réseau est Vab =
V0, on peut écrire :
Vde =V0/(1+ β) et exprimer le coefficient β en fonction de RT , R1 et R2.
6) Exprimer la tension Vn après n cellules élémentaires en fonction de V0,
β et n.
7) On suppose R1 =R2. Au bout de combien de cellules peut-on écrire : Vn
< 10−2×V0 ?
8) Pour une cellule élémentaire de longueur ∆x = 10−5 m, on prendra pour
valeurs R1 =3,5×105 Ω et R2 =1,1×109 Ω. Calculer la résistance totale RT
et le coefficient β pour un axone « infiniment » long. Déterminer
l’atténuation Vn/V0 de la différence de potentiel sur une distance x = 2
mm. Une telle fibre peut-elle permettre un transport d’information sur ℓ
= 1 m?
9) En réalité, l’axone permet le transport de l’information sur une
distance de plusieurs cm. La structure de l’axone est donc plus complexe.
Quel est le paramètre du modèle qu’il faudrait modifier pour tenir compte
du fonctionnement réel de l’axone ? Déterminer sa valeur pour que
l’atténuation Vn/V0 soit de 0,9 pour une distance de 2 mm. (On cherchera
à simplifier RT)
Problème III : Etude d’un circuit récepteur en régime sinusoïdal
Le circuit de la Figure III.1
représente un circuit
récepteur qui est alimenté
sous une tension sinusoïdale
de valeur efficace E = 127 V
en absorbant un courant I à la
pulsation ω = 100π.
1.a) Déterminer les
impédances complexes Z1, Z2
et Z3 de chaque branche de ce circuit.
b) Déterminer l’impédance complexe du récepteur sous la forme :
Z = (A+ jB)/(C+ jD)
c) En fonction des éléments du montage, détailler les expressions
littérales de A, B, C et D sous la forme de polynômes en ω.
4
rl
RC
L
~
e(t)
i
1
(t)
i
2
(t)
u(t)
i(t) rl
RC
L
~
e(t)
i
1
(t)
i
2
(t)
u(t)
rl
RC
L
~
e(t)
i
1
(t)
i
2
(t)
u(t)
i(t)
Figure III. 1

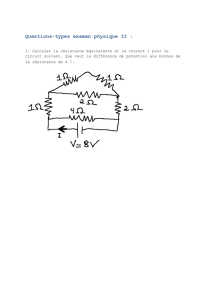
2. Les éléments du récepteur ont les valeurs suivantes : r = 2 Ω, lω = 1 Ω,
R = 5 Ω, Lω = 3 Ω, 1/Cω = 2 Ω. Calculer l’expression numérique de
l’impédance Z après avoir déterminé les termes A, B, C et D.
Déterminer alors numériquement le module Z et l’argument ϕ de
l’impédance.
3. Déterminer le module et l’argument de i, puis l’expression du
courant i(t).
4.a) Déterminer l’expression complexe de la tension u, en fonction de e et
de i.
b) Tracer minutieusement le diagramme de Fresnel associé aux
grandeurs e, u, i, i1 et i2. Prendre les échelles suivantes: 1cm pour 10 V, et
1cm pour 4 A.
Remarques : On choisira E comme origine des phases. On placera I
avec les valeurs calculées précédemment. On construira ensuite U, I1 et
I2.
c) En déduire le signe des déphasages ϕ1 et ϕ2 entre e(t) et les courants
i1(t) et i2(t) respectivement, et ϕu entre e(t) et la tension u(t).
d) En déduire les valeurs efficaces de i1(t), i2(t) et u(t).
5. Calculer par deux méthodes, la puissance active consommée par le
circuit récepteur. Pour l’une des méthodes, vous ferez un tableau qui
indiquera la puissance active de chaque élément du circuit. Vous
donnerez leurs expressions littérales, puis leurs résultats numériques
correspondants.
6. En utilisant le diagramme de Fresnel, déterminer la valeur de la
capacité Cc de compensation à placer en parallèle avec l’impédance Z
pour obtenir un comportement résistif vis à vis du réseau d’alimentation.
5