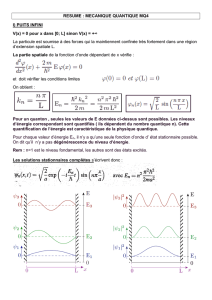
Puits quantiques et super-réseaux semi-conducteurs 1 Puits

Mines Deuxième année
Physique de la matière condensée et des nano-objets
TD8-2011
Puits quantiques et super-réseaux semi-conducteurs 1
Résumé
Dans ce TD nous allons aborder la physique des puits quantiques et des super-réseaux de semi-conducteurs,
dont les applications en électronique et en optique sont multiples.
1 Puits quantiques et super-réseaux
1.1 Définition et fabrication
Les puits quantiques et super-réseaux sont des empilements de couches cristallines alternées, pouvant être aussi
minces que quelques monocouches atomiques, de semi-conducteurs de compositions chimiques différentes.
La fabrication de ces structures se fait à l’aide de technique d’épitaxie par jet moléculaire (Molecular Beam
Epitaxy : MBE) comme illustré ci-dessous
FIGURE 1 – Principe d’une expérience d’épitaxie par jets moléculaires.
Les conditions de croissance de ce type de structure sont assez strictes. Il faut notamment que les paramètres
de maille et structures cristallines soient relativement proches. Mais lorsque les couches sont "compatibles"
on peut faire varier à volonté leur épaisseur. Un système très répandu est GaAs/AlxGa1−xAs pour lequel le
désaccord de maille est faible comme on le voit sur la figure suivante :
1.2 Propriété physique paradoxale
Les deux matériaux étant différents ils n’ont pas la même valeur de bande interdite. Par exemple dans GaAs le
gap vaut 1,42eV alors que dans Al0,4Ga0,6As il est de 2eV. De telles structures possèdent une propriété physique
paradoxale : on s’attendrait à ce que le seuil d’adsorption soit celui du matériau à plus faible bande interdite,
autrement dit qu’un puits quantique soit moins transparent que chacun de ses constituant. L’expérience montre
qu’il n’en est rien.
1. Inspiré de l’ouvrage de B. Sapoval et C. Hermann "Physique des semi-condcuteurs"
1

FIGURE 2 – Relation entre matériaux, structure atomique, paramètre de maille et gap électronique.
1.3 Modélisation
Le potentiel agissant sur un électron d’une telle structure est différent dans les deux matériaux et l’on s’attend
à ce que la structure de bandes et notamment le bas de la bande de conduction et le haut de la bande de valence
soient situées à des énergie différentes comme illustré sur le schéma ci-dessous :
FIGURE 3 – Puits quantique
La modélisation d’une telle structure utilise la théorie de la masse effective qui consiste à décrire les élec-
trons du bas de la bande conduction (et symétriquement les trous du haut de la bande de valence) comme des
particules de masse effective m∗comme indiquÃl’ sur le schéma de la figure 3.
Dans cette théorie la fonction d’onde de l’électron peut s’écrire approximativement :
Ψ(r
r
r) = Ψk
k
k0(r
r
r)φ(r
r
r)
−~2
2m∗4+V(z)φ(r
r
r) = εφ(r
r
r)
m∗est la masse effective (et rend compte de la courbure à l’extremum) des électrons de conduction. Elle dépend
en principe du matériau mais nous négligerons sa variation. V(z)est un potentiel de confinement qui ne dépend
que de z:
2

FIGURE 4 – Electrons et trous de masse effective m∗
c,m∗ v
FIGURE 5 – Potentiel de confinement V(z)
2 Puit quantique
2.1 Forme des fonctions d’ondes
Question no 1 : Montrer que les solutions de l’équation de Schrödinger peuvent s’écrire
φ(r
r
r) = φk
k
k,n(r
r
r) = 1
√Seik
k
k.ρ
ρ
ρχn(z)
ε=εk
k
k,n=~2k2
2m∗+εn
Avec
k
k
k= (kx,ky);ρ
ρ
ρ= (ρx,ρy);S=LxLy
Et χn(z)est solution de l’équation de Schrödinger unidimensionnelle :
−~2
2m∗
d2
dz2+V(z)χn(z) = εnχn(z)
Question no 2 : En utilisant la parité du potentiel montrer que les solutions unidimensionnelles
χn(z)sont soient paires, soient impaires et s’écrivent :
χn(z) = Asin(knz)ou χn(z) = A0cos(knz)pour |z|<L/2
3

Question no 3 : Quelle est la forme des solutions pour |z|>L/2. Quelles sont les conditions de
raccordement ? Montrer que ces conditions conduisent à des solutions discrètes du vecteur d’onde
knqui s’obtiennent par une construction géométrique simple.
2.2 Solution générale
Dans le cas général il y’a un nombre fini d’état liés de fonction d’onde alternativement paire et impaire. On
peut en fait montrer que le nombre d’état lié est donné par n(L) = 1+E[q2m∗
π2~2V0L2],Eétant la partie entière.
Question no 4 : Discuter du nombre d’états liés en fonction des paramètres du problème. Que
se passe-t-il dans la cas extrème d’un puits infini de largeur infiniment petite tel que V0Lreste
constant ? A quel genre de potentiel cela correspond-il ?
Question no 5 : Dans le cas du puits infini (V0=∞) montrer qu’il existe un nombre infini (dénom-
brable) de solutions données par :
χn(z) = q2
Lsinnπz Ln=2p+2p∈IN
χn(z) = q2
Lcosnπz Ln=2p+1p∈IN
εn=~2
2m∗nπ L2
2.3 Discussion physique
Dans le cas de GaAs la masse effective des électrons de conduction est m∗=0.067m0.
Question no 6 : Evaluer l’énergie du premier niveau occupé pour un puits quantique de barrière
infinie et d’épaisseur L=100Å.
Question no 7 : Expliquer pourquoi le puits quantique de GaAs/AlGaAs est plus transparent que
GaAs tout seul.
On rappelle que dans un modèle d’électrons libres le vecteur d’onde de Fermi kFet la densité électronique
nsont reliés par la relation :
n=k3
F
3π2
Question no 8 : Montrer que la longueur d’onde de Fermi λFpour un semiconducteur de densité
électronique 1025m3, est de l’ordre de la centaine d’Angstrom. Expliquer pourquoi il est plus facile
de voir des effets de confinements sur un semiconducteur que sur un métal.
3 Super réseau
Il est possible d’effectuer des multicouches alternées de semi-conducteurs pour former des super-réseaux avec
une périodicité ; donnée comme sur la figure 6 :
Question no 9 : Comment se comporte à votre avis les niveaux énergétiques des différents états
liés ? Montrer comment utiliser le modèle des liaisons fortes pour ce type de structure.
4

FIGURE 6 – Super réseau
FIGURE 7 – minibandes d’un super réseau
Nous avons illustré ci-dessous la notion de mini-bande
Les puits quantiques et super-réseaux ont de nombreuses applications en électronique (diode tunnel réson-
nante..) et en optique (lasers, détection ou émission infra-rouge..) car on peut ajuster presque "à la la demande"
les propriétés physiques de ces matériaux. On appelle cela de "l’ingénierie de structure de bandes" ou plus
communément du "band gap engineering".
5