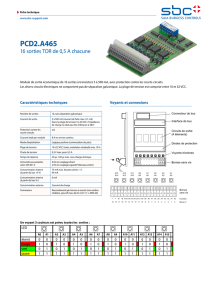
Tests cosmologiques de la gravité massive.

π
DGP

DGP
M
K
0
Σ(l)
3
Ky(r)z(r) 0
r= 0

1
3/4
T=gµν Tµν =ρ+ 3p
DGP

π→π+bµxµ+c
π bµc
S[˜ hµν , π] = Zd4x(LGR +Lπ)
Lπ=Lgalileon(π, ∂π, ∂∂π) + πT
Lgalileon
π→π+bµxµ+c
4
Lgalileon(π, ∂π, ∂∂π) =
5
X
i=1
ciLi(π, ∂π, ∂∂π)
ci

L1=π
L2=−1
2(∂π)2
L3=−1
2∂2π(∂π)2
L4=−1
2(∂2π)2−(∂∂π)2(∂π)2
L5=−1
2(∂2π)3−3(∂2π)(∂∂π)2+ 2(∂∂π)3(∂π)2
δ
δπ Zd4xLi(π, ∂π, ∂∂π) = i(π, ∂π, ∂∂π)
i(π, ∂π, ∂∂π)=(i−1)!δµ1
[ν1···δµi−1 νi−1](∂µ1∂ν1π)···(∂µi−1∂νi−1π)
1= 1
2=∂2π
3= (∂2π)2−(∂∂π)2
4= (∂2π)3−3∂2π(∂∂π)2+ 2(∂∂π)3
5= (∂2π)4−6(∂2π)2(∂∂π)2+ 8∂2π(∂∂π)3+ 3[(∂∂π)2]2−6(∂∂π)4
−1
2∂2˜
hµν −1
2˜
hηµν +··· = 8πGTµν
5
X
i=1
cii(π, ∂π, ∂∂π) = −T
π˜ h
hµν =˜ hµν + 2πηµν