S2 : Notion de signal - Lycée Henri Poincaré PCSI 1 année 2016-2017

S2: Notion de signal
PCSI 2016 – 2017
Au laboratoire et dans la vie de tous les jours, il existe de nombreuses grandeurs physiques dont
la mesure permet d’accéder à des informations. On peut citer par exemple les thermomètres à
alcools. Via la mesure de la hauteur de liquide dans le thermomètre, on en déduit (grâce à un
étalonnage préalable) la température du thermomètre.
I Signaux
Définition : On appelle signal une grandeur physique dont la détermination permet
d’accéder à une information désirée.
Cette notion de signal est subjective puisque ce qui est une information désirée pour un observa-
teur peut être parasite pour un autre. Exemples : le wifi de mon voisin est du bruit pour moi alors
que c’est du signal pour lui, le voisin qui écoute la radio alors que j’essaye de travailler,. . .
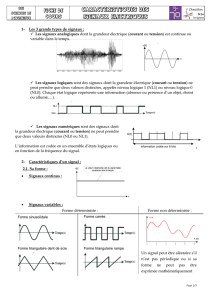
Exemples de signaux dans différents domaines : Voici quelques exemples de domaines de la
physique et des grandeurs correspondantes.
Signal Exemple de situation Grandeur(s) associée(s)
Acoustiques hauts parleurs variation de pression (P)
Électriques réseau domestique par CPL tension (U)
Électromagnétique Radio Champ électromagnétique ( ~ E;~ B)
Optique (cas part. E.M.) Fibre optique Champ électromagnétique (~ E;~ B)
Remarques :
• Il est possible de transformer un signal physique en un autre en utilisant un transducteur.
• Les signaux électriques sont particulièrement intéressant car on peut facilement les acqué-
rir puis les traiter à l’aide d’un ordinateur. On utilise donc fréquemment des transducteurs
permettant de convertir un signal en signal électrique et réciproquement (exemple : micro
et haut-parleurs).
II Cas particulier des signaux périodiques
Définition : On appelle signal périodique un signal qui se répète identique à
lui même au bout d’un certain temps. Le plus petit temps au bout duquel le signal se
répète est appelé période , souvent notée T. La fréquence est l’inverse de la période
f=1
Tet son unité est le Hertz (Hz).
1

S2Notion de signal
t
s(t)
TT
Vpp
Ordres de grandeurs : Il est utile de connaitre quelques ordres de grandeurs de fréquences dans
les différents domaines de la physique :
• En acoustique, on considère en générale que l’oreille peut capter les sons entre 20 Hz et
20 kHz. Les ultrasons qui peuvent être utilisés pour sonder des matériaux peuvent aller
de quelques dizaines de kHz à quelques dizaines de MHz.
• Au laboratoire, les fréquences utilisées par dans les circuits électriques vont de quelques Hz
à quelques centaines de kHz.
• En électromagnétisme, les fréquences varient sur une grande plage : quelques dizaines
de Hz pour certaines tensions, quelques centaines de MHz pour les ondes radio et
quelques GHz pour les téléphones portables et le wifi.
• L’optique correspond à des ondes électromagnétique à beaucoup plus hautes fréquences :
environ 1014 −1015 Hz pour le visible, un peu moins pour l’infrarouge et un peu plus
pour l’ultraviolet.
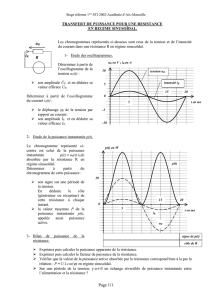
III Caractéristiques d’un signal périodiques
Les principales caractéristiques d’un signal ont été vues sur l’exemple du signal sinusoïdal dans le
chapitre précédent (amplitude, période, valeur moyenne, fréquence, pulsations). On peut rajouter
la grandeur amplitude crête-à-crête qui correspond à Spp =smax −smin (pp pour peak-peak)
retour au schéma
Remarque : Attention, les mesures automatiques de l’oscilloscope annonce parfois amplitude
alors que la grandeur mesurée est l’amplitude peak-peak, pensez donc à vérifier.
Pour étendre la notion de valeur moyenne vue pour un signal sinusoïdal, on utilise la définition
suivante :
Définition : On appelle valeur moyenne d’un signal s(t)périodique la grandeur notée
hs(t)iet dont l’expression est :
hs(t)i=1
TZτ+T
τs(t)dt
Le temps τest un temps quelconque, on choisit fréquemment 0.
Exemple : Calculer la valeur moyenne pour
1. un signal créneau TTL (5 V pendant une demi-période puis 0 V l’autre demi-période)
2. un signal sinusoïdal quelconque.
b
PCSI 2016 – 2017 Page 2/4

S2Notion de signal
Signal créneau TTL : 1
TRT
0s(t)dt =1
TRT/2
0Udt =1
TUT 2=U/2
Signal sinusoïdal quelconque : s(t) = A+Bcos(ωt +ϕ):1
TRT
0s(t)dt =1
TRT
0Adt +1
TRT
0Bcos(ωt +
ϕ)dt =A+h−B
ωsin(ωt +ϕ)iT
0=Acar Test la période, donc même valeur en 0 et en T
Aspect énergétique : La plupart du temps, les grandeurs énergétiques associées à un signal
dépendent du signal de façon quadratique , c’est-à-dire proportionnelle à s(t)2. Ainsi, un
signal de valeur moyenne nulle peut correspondre à une énergie de valeur moyenne non nulle.
Par exemple l’énergie cinétique dans le cas de l’oscillateur harmonique : la vitesse est en moyenne
nulle, mais pas l’énergie cinétique. La grandeur pertinente est alors hs(t)2i, mais elle est homogène
non pas à smais à s2.
Définition : La valeur efficace d’un signal s(t)est la grandeur
Seff =qhs(t)2i=s1
TZτ+T
τs(t)2dt
Sa dimension et son unité sont les mêmes que celles de s(t).
Remarques :
• Cette grandeur est parfois appelée valeur RMS (root mean square).
• La valeur efficace d’un signal dépend non seulement de son amplitude, mais aussi de sa
forme.
Par exemple, calculer la valeur efficace pour :
1. un signal créneau de valeur moyenne nulle et d’amplitude 2 V
2. un signal sinusoïdal de même amplitude et de valeur moyenne nulle.
b
1. s2=cte =U2⇒ hs2i=U2⇒seff =U
2. s2=U2cos2(ωt) = U21+cos(2ωt)
2⇒ hs2i=U21+0 2⇒seff =U/√2
IV Spectre d’un signal périodique
Définition : Un signal est dit monochromatique s’il est sinusoïdal. Dans le cas
contraire, il est dit polychromatique.
PCSI 2016 – 2017 Page 3/4

S2Notion de signal
Un signal périodique polychromatique peut être décomposé comme la somme de plusieurs co-
sinus. Cette décomposition s’appelle décomposition en série de Fourrier. Par exemple, un signal
triangulaire peut s’exprimer de la façon suivante :
+∞
X
i=0
1
(2i+ 1)2cos ((2i+ 1) ×2πf t)
.
t
s(t)
=t+t+t+. . .
De façon plus générale, un signal périodique de fréquence f0peut s’exprimer sous la forme
+∞
X
n=0
cncos (n×2πf0t+ϕn)
Définition : Le spectre d’un signal est l’amplitude cndes cosinus, dans sa décompo-
sition de Fourrier, en fonction de la fréquence.
Remarque : Il s’agit ici d’une première introduction et cette notion sera revue lors du filtrage.
Dans le cas d’un signal périodique, le spectre du signal a donc une allure de bâtons de
différentes amplitudes à des fréquences qui sont un multiple entier de la fréquence du si-
gnal. Par exemple dans le cas du signal triangulaire précédent, on obtient le spectre ci-dessous
à gauche. Comme les différentes amplitudes décroissent en général rapidement, il est fréquent de
représenter le logarithme de l’amplitude en fonction de la fréquence (figure ci-dessous à droite)
f
cn
1f03f05f07f0f
ln(cn)
1f03f05f07f0
Pour un signal plus complexe, le spectre obtenu peut
prendre l’allure d’une courbe et non plus de bâton-
net. Par exemple, si l’on étudie la lumière provenant
d’un néon, on obtient la courbe ci-contre. (1 THz cor-
respond à 1012 Hz )
L’opération qui permet de passer d’un signal à son
spectre s’appelle transformée de Fourrier.
Sur les appareils de mesures, il faut généralement
chercher la fonction appelée FFT (Fast Fourrier Transform).
PCSI 2016 – 2017 Page 4/4

S2Notion de signal
Table des matières
I Signaux
II Cas particulier des signaux périodiques
III Caractéristiques d’un signal périodiques
IV Spectre d’un signal périodique
PCSI 2016 – 2017 Lycée Poincaré