Exercices montages utilisants l`a.o.p.

1APPLICATIONS DE L’AMPLIFICATEUR OPERATIONNEL 1° PARTIE
Tous les montages proposés utilisent un amplificateur opérationnel idéal fonctionnant en mode
linéaire. La tension d’excitation ve est sinusoïdale.
AMPLIFICATEUR A GAIN AJUSTABLE
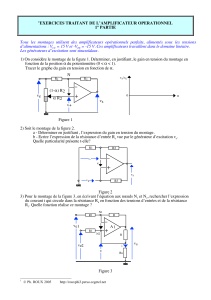
1. Le montage de la figure 1 est un amplificateur inverseur à gain variable, possédant une
résistance d’entrée fixe égale à R1. Calculer l’expression du gain en tension
Av
v
s
e
=
A en
fonction des éléments du montage et de la position a du potentiomètre R3. Négliger le
courant i dans R2 devant le courant is qui circule dans R3 et R4.
a R3
0 ≤ a ≤1
vs
ve
eA0
R4
N
R2
R1
v
i
is
Figure 1
2. On donne : R1 = 10KΩ, R2= 100KΩ, R3 = 5KΩ, R4 = 1KΩ. Calculer la valeur du gain A
pour les positions extrêmes du potentiomètre R3.
AMPLIFICATEUR A RESISTANCE D’ENTREE ELEVEE
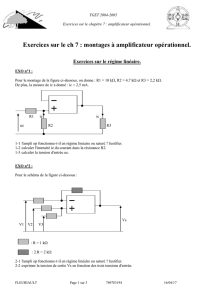
3. On considère le montage de la figure 2.
vs1
ve
i
R1
R2
R
2 R1
R2
vs2
A1
A2
Figure 2
a. Déterminer l’expression des gains en tension :
Gv
v
s
e
1
1
=
et
Gv
v
s
e
2
2
=
.
1Philippe ROUX © 2006 http://rouxphi3.perso.cegetel.net

2
b. Calculer la résistance d’entrée Re du montage vu par le générateur d’attaque ve puis
calculer la valeur de R permettant d’obtenir Re = 100 KΩ sachant que : R1 = 10KΩ et
R2 = 100 KΩ.
MONTAGE SIMULATEUR DE SELF-INDUCTANCE
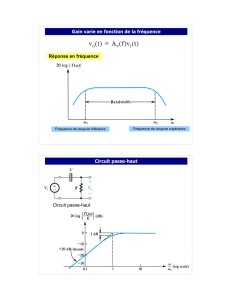
4. Le montage de la figure 3 constitue un simulateur de self-inductance.
R
C
B
A2
ve
i
vs2 vB
A
vA
vs1
R
R
e
e
A1
R
Figure 3
a. En exploitant les propriétés essentielles de l’amplificateur opérationnel, que pensez-
vous des tensions vA et vB vis à vis de ve ? Quelle relation simple lie la tension vs2 à
la tension ve et au courant i ?
b. Rechercher la relation liant les tensions vB et vs1.
c. En écrivant l’équation au nœud A, chercher une autre relation reliant vs2 et ve.
d. Déduire des questions précédentes, l’expression de l’impédance d’entrée Ze = ve /i
du montage et montrer qu’il s’agit d’une self-inductance L dont on donnera
l’expression en fonction de R et C.
e. Faire l’application numérique pour R = 10 kΩ et C = 0,1 µF.

3
2APPLICATIONS DE L’AMPLIFICATEUR OPERATIONNEL 2° PARTIE
Tous les montages proposés utilisent des amplificateurs opérationnels idéaux et le générateur
parfait de tension d’excitation eg délivre une tension sinusoïdale : eg =Egm sin ( ω t).
MONTAGE AMPLIFICATEUR INVERSEUR, NON-INVERSEUR
R
R
2
R
K
+
-
eg
vs
e
2R
1. Déterminer le gain en tension [vs / eg] du montage donné ci-dessus pour les deux
positions de l’interrupteur K.
a. L’interrupteur K est ouvert.
b. L’interrupteur K est fermé.
MONTAGE MULTIPLIEUR DE CAPACITE
Le montage suivant qui utilise deux amplificateurs opérationnels possède une impédance
d’entrée purement capacitive dont on propose de calculer l’expression en fonction de la
position α du potentiomètre R.
A1A2
+
-
eg
ee
α R (1- α)
R
i
g
C
vs
2
vs1
2. Déterminer l’expression des gains en tension [vs1/eg] et [vs2/vs1] des deux étages.
3. En déduire l’expression de l’impédance d’entrée Ze du montage vue par le générateur
d’excitation et montrer que le montage est un “multiplieur de capacité”.
Application numérique : calculer la position du potentiomètre pour obtenir un facteur
de multiplicatif de 10.
2Philippe ROUX © 2006 http://rouxphi3.perso.cegetel.net

MONTAGE SIMULATEUR DE SELF INDUCTANCE
Le montage suivant possède, sous une condition à déterminer, une impédance d’entrée vue par le
générateur d’excitation eg, purement selfique.
A2
A1
R3
R2
R1
R
4
R5
C
+
-
eg
vs2
vs1
ee
i
g
v1+
N1N3
N2
4. Ecrire les équations aux noeuds N1, N2 et N3 ( on peut utiliser les conductances Gi des
résistances).
5. Quelle relation simple lie les tensions V1+ et eg ?
6. En déduire l’expression de l’admittance entrée Ye du montage vue par le générateur
d’excitation eg.
7. Quelle condition doit-on satisfaire pour que l’admittance d’entrée soit purement selfique ?
Quelle est alors l’expression de la self L simulée ?
8. Application numérique : on donne C = 0.1 µF, R4 =1 KΩ, R3 = 10 KΩ, R2 = R5 = 100
KΩ. Calculer la valeur de la self-inductance et de la résistance R1.

3APPLICATIONS DE L’AMPLIFICATEUR OPERATIONNEL 3° PARTIE
MONTAGE SIMULATEUR DE SELF-INDUCTANCE
On considère le montage de la figure 1 qui utilise un amplificateur opérationnel A1 idéal
utilisé en mode linéaire et alimenté par deux tensions d’alimentation +VCC = +15 V et –VEE = -15 V.
Le montage est excité par une tension sinusoïdale ve telle que l’amplitude maximale de la tension de
sortie Vs1 soit égale à 15 V.
A1
20 KΩ
20 KΩ10 KΩ
R1
R
R
eve
i1
E1
vs1
Figure 1
1. Déterminer l’expression du gain en tension Av1 = [vs1/ve] du montage. Faire l’A.N.
En déduire la valeur de l’amplitude maximale Vem de la tension d’entrée qui permet à l’A.O.P.
de fonctionner en régime linéaire.
2. Déterminer dans ces conditions, l’expression de la résistance négative d’entrée
Rv
i
e
e
1
1
=
du
montage vue par la tension ve entre l’entrée E1 et la masse.? Faire l’A.N.
On considère maintenant le montage de la figure 2 qui est excité par la tension ve, dans les mêmes
conditions que le montage précédent.
R1
R
R
Ru
e
A
i2
is
E2
A2
B
R1
10 kΩ20 kΩ20 kΩ
10 kΩ
10 kΩ
ve
vA
vs2 vB
Figure 2
3Philippe ROUX © 2006 http://rouxphi3.perso.cegetel.net