Optique Géométrique

L1 - UE LP 103 – Optique géométrique – TD 3 - 16/11/09 1/3
Université Pierre et Marie Curie - L1 - UE LP 103 - Année 2009-2010
[email protected]
Optique Géométrique - TD Série N°3
Instruments optiques ; angles solides ; énergie lumineuse
Certains exercices ont été préparés avec la collaboration de J. Lasue et M. Cabane
1) Doublet de lentilles (extrait sujet juin 2005)
Un système optique grossissant comporte deux lentilles L1 et L2 : L1, objectif, est une lentille
convergente de distance focale f'1 = + 3 cm. L2, oculaire, est une lentille divergente de
distance focale image f'2=-6 cm. Leur centre optique, respectivement O
1
et O
2
, sont séparés
de O
1
O
2
= +9cm.
1. Un observateur, ayant une vue normale (punctum remotum à l'infini, punctum proximum à
20 cm) désire observer sans fatigue, au travers du système grossissant.
1a. Où doit se former l'image définitive A'B' donnée par l'ensemble des deux
lentilles (A sur l'axe optique, B hors de l'axe)?
Où doit alors se former l'image intermédiaire A
1
B
1
donnée par L1 de l'objet AB ?
1b. Faire un schéma à l'échelle représentant les deux lentilles :
- Positionner les foyers image et objet des deux lentilles.
- Trouver par construction la position de l'objet réel B correspondant à l'image définitive B'.
- Expliquer les constructions.
1c. Retrouver par le calcul la distance O
1
A.
2. 2a. Sous quel angle α serait vu au mieux, à l'oeil nu, l'objet AB ?
2b. Sous quel angle α' est vue l'image A'B' donnée par le système ?
2c. Calculer le grossissement apporté par le système.
2) Téléobjectif.
Un téléobjectif est constitué de la façon suivante :
- une lentille L
1
(f
1
’=75mm) de centre O
1
, la pellicule étant dans le plan focal image de
celle-ci.
- une lentille L
2
(f
2
’=-25mm) est collée à L
1
.
- une lentille L
3
(f
3
’=100mm) de centre O
3
, est placée en avant de {L
1
, L
2
}. La distance
O
1
O
3
est réglée de telle façon qu’un objet très loin soit net sur la pellicule.
a) Faire le schéma complet, calculer O
1
O
3
et en déduire la taille de ce téléobjectif.
b) Quelle est la taille sur la pellicule d’une tour de 60 m située à 3 km ?
c) Déterminer la taille d’un appareil qui donnerait la même image avec une seule lentille.
Comparer.
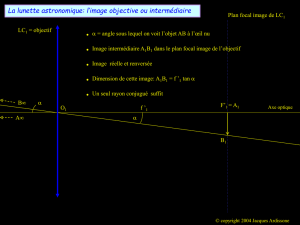
3) Lunette astronomique
Une lunette astronomique est formée de deux lentilles : L
1
l’objectif, L
2
l’oculaire. f
1
’=80cm,
f
2
’=2cm. Ce type d’instrument est afocal. Déterminer la distance O
1
O
2
pour qu’il en soit ainsi.
Un objet à l’infini donne donc une image à l’infini. Soit α le diamètre angulaire d’une planète
et α’ le diamètre angulaire de son image à travers la lunette. Où se trouve l’image de la
planète par L
1
? Déterminer le grossissement de la lunette : G=α’/α.
Si maintenant on désire, avec cette lunette, regarder un objet à la distance d de l’objectif. Où
se trouve maintenant l’image de cet objet par L
1
(comparer à la position de l’image de la
planète) ?
De combien faut-il déplacer l’oculaire et dans quelle direction pour que l’image de cet objet
par la lunette soit à l’infini ?

L1 - UE LP 103 – Optique géométrique – TD 3 - 16/11/09 2/3
4) Lunette d’observation
Dans le montage initial, la lunette astronomique donne une image renversée de l’objet, ce qui
est regrettable dans le cas d’observation terrestre. On se propose donc de « redresser » cette
image en interposant entre L
1
et L
2
une lentille convergente L
3
de distance focale O
3
F’
3
= f
3’
=
2 cm. Cette lentille doit donner de A
0
B
0
– image de AB à travers L
1
– une image réelle A
1
B
1
renversée et plus grande par un facteur |γ| > 1 L’oculaire doit être alors déplacé pour donner
de cette nouvelle image (A
1
B
1
) une image définitive à l’infini.
1. Où doit se trouver A
1
B
1
par rapport à L
2
? Préciser ensuite où doit se situer A
0
B
0
par
rapport à L
3
pour satisfaire les conditions d’existence de A
1
B
1
et le grandissement
recherché.
2. Faire un schéma du dispositif expérimental et des rayons lumineux issus de l’objet AB
situé à l’infini.
3. Calculer les distances O
3
A
0
et O
3
A
1
en fonction de γ et de f
3’
.
4. De combien a augmenté la longueur (distance O
1
O
2
) de la lunette ?
5. Calculer le grandissement angulaire (ou grossissement) G’ de la lunette. Calculer le
rapport G’ / G. AN : |γ|= 3.
6. Connaissez-vous une autre méthode expérimentale pour réaliser ce type de lunette
donnant une image définitive dans le même sens que l’objet ?
5) Appareil photo
Un appareil photo a un objectif de 20 δ (dioptries) et un diamètre D ; il est réglé sur l’infini.
Montrer graphiquement, en traçant les rayons extrêmes, qu’un point à distance finie d donnera
une tache sur la pellicule. Déterminer le diamètre de cette tache en fonction de D, d et f’ la
focale de l’objectif.
La photo sera nette si un point donne une tache de diamètre inférieur à 20 µm (ce flou ne sera
pas détectable par l’œil). Calculer la distance minimale à laquelle doivent être les objets pour
être nets avec D=25mm, puis D=10mm.
6) Caractéristiques de l’œil.
Quelles lunettes faut-il prescrire :
- à un myope qui ne peut lire un texte qu’éloigné de ses yeux de 20cm au maximum ?
- A un hypermétrope qui ne peut lire un texte qu’éloigné de ses yeux de 50cm au
minimum ?
Un homme a une vision normale dans l’eau. Est-il myope ou hypermétrope ?
7) Lunette astronomique et observation des étoiles
Une lunette astronomique, montée en système afocal, est utilisée pour observer une étoile,
assimilable à un objet ponctuel placé à l'infini. Soient f1’ et f2’ les distances focales image de
l'objectif et de l'oculaire. Dans le cas de la grande lunette de l'observatoire de Meudon: f1’
=16 m et f2’=4cm.
1) Exprimer le grossissement G en fonction de f1’ et f2’. Les rayons lumineux provenant de
l'étoile arrivent sur l'objectif de diamètre D (D=80cm à Meudon); l'orientation de la lunette est
telle que ces rayons sont parallèles à son axe optique. Quel est le diamètre d du faisceau
lumineux qui sort de la lunette? Un observateur place son oeil contre l'oculaire, le rayon de sa
pupille est a≈2mm. Où se forme l'image finale de l'étoile? Doit-il accommoder pour voir
l’image de la planète ?
2) Soit E l'éclairement produit par cette étoile sur la surface terrestre, exprimer, en fonction de
E, a et D
a) le flux lumineux Φ
0
reçu par l'oeil de l'observateur s'il regarde l'étoile à l'oeil nu,

L1 - UE LP 103 – Optique géométrique – TD 3 - 16/11/09 3/3
b) le flux lumineux Φ
L
reçu par l'oeil dans le cas où l'observation se fait à l'aide de la
lunette astronomique définie plus haut.
c) En déduire le rapport Φ
L
/ Φ
0
.
3) Si le flux lumineux reçu par l'oeil, en provenance d'une étoile, est inférieur à Φ
m
≈ l,5 10
-17
watt, il n'y a pas d'excitation de cellule rétinienne, et l'étoile n'est pas vue. Traiter les cas de
l'étoile Proxima du Centaure (E
pc
≈ 10
-14
Wm
-2
) et de l'étoile polaire (α Petite Ourse E
po
≈3,510
-11
W m
-2
).
8) Panneaux solaires
Dans un modèle simplifié du système solaire on peut admettre que les planètes ont des orbites
circulaires autour du Soleil. La distance Soleil-Terre est ST≈ 1,5 l0
11
m, cette distance définit
l’unité astronomique. Le Soleil peut être assimilé à une source ponctuelle, émettant
isotropiquement dans tout l'espace une puissance P≈3,9 10
26
watts.
On sait convertir la puissance rayonnée par le Soleil en puissance électrique utilisable à l'aide
de cellules photo-électriques, regroupées en panneaux solaires. Le rendement ρ d'un tel
système est environ 10%: à partir d'un watt arrivant sous forme de photons on obtient 0,1 watt
électrique utilisable.
1) A midi, heure solaire, à l'équateur, on place face au Soleil, S, sur le sol terrestre un panneau
plan de surface Σ=1 m
2
(en d'autres termes: la normale à Σ est confondue avec la direction
TS). a) Quel est l'angle solide (en stéradians) sous lequel on voit Σ, si on est placé en S?
b) Quel est le flux lumineux Φ à travers Σ? Quelle est la puissance électrique P
l
dont
on pourrait disposer avec un tel panneau? La traversée de l'atmosphère terrestre
conduit en fait à une perte de 25% du flux solaire, quelle est la puissance P
u
disponible en réalité?
c) La Terre tourne sur elle même en 24h, quels sont, dans les hypothèses précédentes,
le flux à travers Σ et la puissance disponible à 8h? à 16h?
2) De tels panneaux solaires sont souvent installés sur les sondes spatiales, et orientés en
permanence vers le Soleil, pour fournir de l'énergie aux instruments de mesure et de
transmission de données placés à bord/ Une valeur typique de la puissance nécessaire au bon
fonctionnement est P
s
=700 watts.
a) dans ces conditions quelle est la surface Σ
TV
de panneaux, de rendement ρ=10%,
nécessaire pour mener à bien une mission Terre-Vénus (Soleil-Vénus ≈ 1,1 10
11
m)?
b) et pour une mission Terre-Saturne (Soleil-Saturne ≈ 1,5 10
12
m) ?